Triangulierung (Topologie)
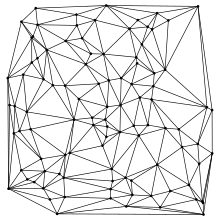
In der Topologie, einem Teilgebiet der Mathematik, ist eine Triangulierung (oder Triangulation) eine Zerlegung eines Raumes in Simplizes (Dreiecke, Tetraeder oder deren höher-dimensionale Verallgemeinerungen).

Definition[Bearbeiten | Quelltext bearbeiten]
Eine Triangulierung eines topologischen Raumes ist gegeben durch einen (abstrakten) Simplizialkomplex und einen Homöomorphismus
- ,
der geometrischen Realisierung auf .
Triangulierbarkeit von Mannigfaltigkeiten[Bearbeiten | Quelltext bearbeiten]
Die Triangulierbarkeitsvermutung besagt, dass jede Mannigfaltigkeit triangulierbar ist. Sie wurde 1926 von Hellmuth Kneser aufgestellt.[1] Es gibt jedoch, wie im Folgenden gezeigt wird, Gegenbeispiele zur Triangulierbarkeitsvermutung.
Mannigfaltigkeiten bis zur dritten Dimension sind stets triangulierbar. Das wurde von Tibor Radó 1925 für Flächen und 1952 von Edwin Moise für 3-Mannigfaltigkeiten bewiesen. Auch in höheren Dimensionen sind differenzierbare Mannigfaltigkeiten gemäß dem Satz von Whitehead stets triangulierbar. Einen einfacheren Beweis gab Hassler Whitney mit Hilfe seines Einbettungssatzes.
Alle differenzierbaren und alle stückweise linearen Mannigfaltigkeiten sind triangulierbar. Robion Kirby und Laurence Siebenmann zeigten, dass nicht alle topologischen Mannigfaltigkeiten eine PL-Struktur besitzen. Sie zeigten aber auch, dass es triangulierbare Mannigfaltigkeiten ohne PL-Struktur gibt.
Andrew Casson zeigte mit Hilfe der nach ihm benannten Casson-Invariante, dass 4-Mannigfaltigkeiten mit gerader Schnittform und Signatur 8 nicht trianguliert werden können. Aus Freedmans Arbeit weiß man, dass es eine solche 4-Mannigfaltigkeit gibt. Sie wird genannt. Michael Davis und Tadeusz Januszkiewicz bewiesen, dass man durch Hyperbolisierung von eine nicht-triangulierbare asphärische 4-Mannigfaltigkeit bekommt.
Ende der 70er Jahre konstruierten David Galewski und Ronald John Stern eine Mannigfaltigkeit, die genau dann trianguliert werden kann, wenn jede Mannigfaltigkeit der Dimension trianguliert werden kann. 2013 bewies Ciprian Manolescu, dass die Galewski-Stern-Mannigfaltigkeit nicht trianguliert werden kann. Der Grund dafür ist, dass der Rochlin-Homomorphismus nicht spaltet. Mittels Hyperbolisierung zeigten Michael Davis, Jim Fowler und Jean-François Lafont, dass es in Dimension nicht-triangulierbare asphärische Mannigfaltigkeiten gibt.
Hauptvermutung[Bearbeiten | Quelltext bearbeiten]
Die Frage nach der Eindeutigkeit von Triangulierungen wurde als sogenannte „Hauptvermutung“ bekannt (Heinrich Tietze): Wenn die geometrischen Realisierungen und zweier Simplizialkomplexe homöomorph sind, gibt es dann kombinatorisch isomorphe Unterteilungen der Simplizialkomplexe und ? Die Hauptvermutung, die aussagt, dass es eine solche Unterteilung gibt, ist im Allgemeinen falsch. Erste Hinweise darauf fand John Milnor im Jahr 1961. Milnors Beispiele waren allerdings keine Mannigfaltigkeiten. Erst aus den Arbeiten von R. Kirby und L. C. Siebenmann ergaben sich dann auch Mannigfaltigkeiten als Gegenbeispiele.
Ursprüngliche Motivation für die Hauptvermutung war der Beweis der topologischen Invarianz kombinatorisch definierter Invarianten wie der simplizialen Homologie. Trotz des Scheiterns der Hauptvermutung lassen sich Fragen dieser Art oftmals mit dem simplizialen Approximationssatz beantworten.
Anzahl von Triangulierungen[Bearbeiten | Quelltext bearbeiten]
Die Anzahl der Triangulierungen einer Mannigfaltigkeit kann exponentiell mit der Anzahl der Ecken wachsen. Für die 3-Sphäre wurde das von Nevo und Wilson bewiesen.
Je zwei unterschiedliche Triangulierungen derselben Mannigfaltigkeit lassen sich durch eine Folge von Pachner-Zügen ineinander überführen.
Siehe auch[Bearbeiten | Quelltext bearbeiten]
- Delaunay-Triangulation für Verfahren zur Triangulierung von Teilmengen der Ebene (mit vorgegebenen Ecken)
- Triangulation (Fläche) für Verfahren zur Triangulierung von im Raum liegenden Flächen
Literatur[Bearbeiten | Quelltext bearbeiten]
- Tibor Radó: Über den Begriff der Riemannschen Fläche. Acta Sci. Math. (Szeged), 2(1925), 101–121.
- John Henry Constantine Whitehead: On C1-complexes. Ann. of Math. (2) 41, (1940). 809–824.
- Edwin Moise: Affine structures in 3 -manifolds. V. The triangulation theorem and Hauptvermutung. Ann. of Math. (2) 56, (1952). 96–114.
- Hassler Whitney: Geometric integration theory. Princeton University Press, Princeton, N. J., 1957. (Mit einem Beweis des Satzes von Whitehead.)
- David Galewski, Ronald Stern: Classification of simplicial triangulations of topological manifolds. Ann. of Math. (2) 111 (1980), no. 1, 1–34.
- Michael Freedman: The topology of four-dimensional manifolds. J. Differential Geom. 17 (1982), no. 3, 357–453.
- Michael Davis, Tadeusz Januszkiewicz: Hyperbolization of polyhedra. J. Differential Geom. 34 (1991), no. 2, 347–388.
- Ciprian Manolescu: Pin(2)-equivariant Seiberg-Witten Floer homology and the Triangulation Conjecture pdf
- Michael Davis, Jim Fowler, Jean-François Lafont: Aspherical manifolds that cannot be triangulated. Alg. Geom. Top. 14 (2014), 795–803. Artikel
- John Milnor: Two complexes which are homeomorphic but combinatorially distinct. Ann. of Math. (2) 74, (1961). 575–590
- Robion Kirby, Laurence Siebenmann: On the triangulation of manifolds and the Hauptvermutung. Bull. Amer. Math. Soc. 75 (1969). 742–749
- Eran Nevo, Stedman Wilson: How many n-vertex triangulations does the 3-sphere have? pdf
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Ciprian Manolescu: Lectures on the triangulation conjecture
- Ciprian Manolescu: Triangulations of Manifolds
- Andrew Ranicki: On the Hauptvermutung
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Kneser, Die Topologie der Mannigfaltigkeiten, Jahresbericht DMV, Band 34, 1926, S. 1–14









