In der Mathematik ist die Weyl-Kammer (benannt nach Hermann Weyl ) ein Begriff aus der Theorie der Lie-Gruppen . Weyl-Kammern werden bei der Definition positiver und einfacher Wurzeln benötigt, außerdem spielen sie eine zentrale Rolle in der Theorie der Gebäude .
Sei
g
{\displaystyle {\mathfrak {g}}}
dimensionale halbeinfache Lie-Algebra ,
a
⊂
g
{\displaystyle {\mathfrak {a}}\subset {\mathfrak {g}}}
Cartan-Unteralgebra und
(
a
,
R
)
{\displaystyle ({\mathfrak {a}},R)}
Wurzelsystem .
Für eine Wurzel
α
∈
R
⊂
a
{\displaystyle \alpha \in R\subset {\mathfrak {a}}}
E
α
:=
{
x
∈
a
:
α
∨
(
x
)
=
0
}
⊂
a
{\displaystyle E_{\alpha }:=\left\{x\in {\mathfrak {a}}:\alpha ^{\vee }(x)=0\right\}\subset {\mathfrak {a}}}
die zugehörige Hyperebene in
a
{\displaystyle {\mathfrak {a}}}
Dann heißen die Zusammenhangskomponenten von
a
∖
∪
α
∈
R
E
α
{\displaystyle {\mathfrak {a}}\setminus \cup _{\alpha \in R}E_{\alpha }}
die Weyl-Kammern des Wurzelsystems.
Die Weyl-Gruppe von
g
{\displaystyle {\mathfrak {g}}}
a
{\displaystyle {\mathfrak {a}}}
permutiert die Menge der Weyl-Kammern, d. h., die Wirkung der Weyl-Gruppe auf der Menge der Weyl-Kammern ist einfach transitiv und die Anzahl der Weyl-Kammern ist die Kardinalität der Weyl-Gruppe.
Der Abschluss einer Weyl-Kammer ist ein Fundamentalbereich für die Wirkung der Weyl-Gruppe auf
a
{\displaystyle {\mathfrak {a}}}
Es sei
X
=
G
/
K
{\displaystyle X=G/K}
symmetrischer Raum von nichtkompaktem Typ .
Dann sind alle
x
{\displaystyle x}
Flachs
F
⊂
X
{\displaystyle F\subset X}
F
=
e
x
p
x
(
a
)
{\displaystyle F=exp_{x}({\mathfrak {a}})}
für eine abelsche Unteralgebra
a
⊂
p
{\displaystyle {\mathfrak {a}}\subset {\mathfrak {p}}}
e
x
p
x
:
p
→
X
{\displaystyle exp_{x}\colon {\mathfrak {p}}\to X}
Exponentialabbildung in
x
∈
X
{\displaystyle x\in X}
g
=
k
⊕
p
{\displaystyle {\mathfrak {g}}={\mathfrak {k}}\oplus {\mathfrak {p}}}
Cartan-Zerlegung .)
Insbesondere lässt sich der Begriff der Weyl-Kammern auf Flachs in symmetrischen Räumen übertragen: Weyl-Kammern in
F
{\displaystyle F}
a
{\displaystyle {\mathfrak {a}}}
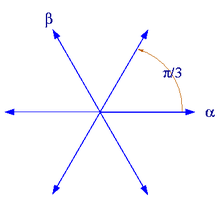
Wurzelsystem A2 Es sei
g
=
s
l
(
3
,
R
)
=
{
A
∈
Mat
(
3
,
R
)
:
Spur
(
A
)
=
0
}
{\displaystyle {\mathfrak {g}}=sl(3,\mathbb {R} )=\left\{A\in \operatorname {Mat} (3,\mathbb {R} ):\operatorname {Spur} (A)=0\right\}}
und
a
=
{
diag
(
λ
1
,
λ
2
,
λ
3
)
:
λ
1
+
λ
2
+
λ
3
=
0
}
{\displaystyle {\mathfrak {a}}=\left\{\operatorname {diag} (\lambda _{1},\lambda _{2},\lambda _{3}):\lambda _{1}+\lambda _{2}+\lambda _{3}=0\right\}}
Das zugehörige Wurzelsystem besteht aus den sechs Wurzeln
α
1
=
diag
(
1
,
−
1
,
0
)
{\displaystyle \alpha _{1}=\operatorname {diag} (1,-1,0)}
α
2
=
diag
(
1
,
0
,
−
1
)
{\displaystyle \alpha _{2}=\operatorname {diag} (1,0,-1)}
α
3
=
diag
(
0
,
1
,
−
1
)
{\displaystyle \alpha _{3}=\operatorname {diag} (0,1,-1)}
α
4
=
diag
(
−
1
,
1
,
0
)
{\displaystyle \alpha _{4}=\operatorname {diag} (-1,1,0)}
α
5
=
diag
(
−
1
,
0
,
1
)
{\displaystyle \alpha _{5}=\operatorname {diag} (-1,0,1)}
α
6
=
diag
(
0
,
−
1
,
1
)
{\displaystyle \alpha _{6}=\operatorname {diag} (0,-1,1)}
entsprechend
α
1
∨
(
diag
(
λ
1
,
λ
2
,
λ
3
)
)
=
λ
1
−
λ
2
{\displaystyle \alpha _{1}^{\vee }(\operatorname {diag} (\lambda _{1},\lambda _{2},\lambda _{3}))=\lambda _{1}-\lambda _{2}}
α
2
∨
(
diag
(
λ
1
,
λ
2
,
λ
3
)
)
=
λ
1
−
λ
3
{\displaystyle \alpha _{2}^{\vee }(\operatorname {diag} (\lambda _{1},\lambda _{2},\lambda _{3}))=\lambda _{1}-\lambda _{3}}
α
3
∨
(
diag
(
λ
1
,
λ
2
,
λ
3
)
)
=
λ
2
−
λ
3
{\displaystyle \alpha _{3}^{\vee }(\operatorname {diag} (\lambda _{1},\lambda _{2},\lambda _{3}))=\lambda _{2}-\lambda _{3}}
α
4
∨
(
diag
(
λ
1
,
λ
2
,
λ
3
)
)
=
λ
2
−
λ
1
{\displaystyle \alpha _{4}^{\vee }(\operatorname {diag} (\lambda _{1},\lambda _{2},\lambda _{3}))=\lambda _{2}-\lambda _{1}}
α
5
∨
(
diag
(
λ
1
,
λ
2
,
λ
3
)
)
=
λ
3
−
λ
1
{\displaystyle \alpha _{5}^{\vee }(\operatorname {diag} (\lambda _{1},\lambda _{2},\lambda _{3}))=\lambda _{3}-\lambda _{1}}
α
6
∨
(
diag
(
λ
1
,
λ
2
,
λ
3
)
)
=
λ
3
−
λ
2
{\displaystyle \alpha _{6}^{\vee }(\operatorname {diag} (\lambda _{1},\lambda _{2},\lambda _{3}))=\lambda _{3}-\lambda _{2}}
Die
E
α
{\displaystyle E_{\alpha }}
α
{\displaystyle \alpha }
α
{\displaystyle \alpha }
Die Weyl-Gruppe ist in diesem Fall die symmetrische Gruppe
S
3
{\displaystyle S_{3}}
Armand Borel : Linear algebraic groups. W. A. Benjamin, New York / Amsterdam 1969Alexander Kirillov Jr.: An introduction to Lie groups and Lie algebras . In: Cambridge Studies in Advanced Mathematics , 113. Cambridge University Press, Cambridge 2008, ISBN 978-0-521-88969-8
Ira Gessel, Doron Zeilberger: Random walk in a Weyl chamber . JSTOR :2159560