Bayessche Statistik
Die bayessche Statistik, auch bayesianische Statistik oder Bayes-Statistik (nach Thomas Bayes ), ist ein Zweig der Statistik, der mit dem bayesschen Wahrscheinlichkeitsbegriff und dem Satz von Bayes Fragestellungen der Stochastik untersucht. Die bayessche Statistik basiert auf der Betrachtung der Wahrscheinlichkeit als „Grad der Überzeugung“, dass ein Ereignis gemäß dem bisherigen Kenntnisstand sowie der vorliegenden Daten auftritt, während die klassische frequentistische Interpretation, Wahrscheinlichkeit als den Grenzwert der relativen Häufigkeit eines Ereignisses nach vielen Versuchen versteht.[1]
Klassische und bayessche Statistik führen oft zu den gleichen Ergebnissen,[2] jedoch setzt der bayessche Wahrscheinlichkeitsbegriff keine unendlich oft wiederholbaren Zufallsexperimente voraus (z. B. bei kleiner Datengrundlage), benötigt dafür aber eine plausible Festlegung der A-priori-Wahrscheinlichkeit für die Nullhypothese.[3] Eine geringe Datenmenge führt dabei zu einer breiten Wahrscheinlichkeitsverteilung, die nicht stark lokalisiert ist.
Aufgrund der strengen Betrachtung von Wahrscheinlichkeitsverteilungen sind bayessche Verfahren oft rechnerisch aufwändig. Dies gilt als ein Grund, weshalb sich im 20. Jahrhundert frequentistische und Ad-hoc-Methoden in der Statistik als prägende Techniken gegenüber bayesschen durchsetzten. Im Zuge der Verbreitung von Computern und Monte-Carlo-Sampling-Verfahren sind komplizierte bayessche Verfahren jedoch möglich geworden.
Im Satz von Bayes wird eine bestehende Erkenntnis über die zu untersuchende Variable (die A-priori-Verteilung, kurz Prior) mit den neuen Erkenntnissen aus den Daten kombiniert („Likelihood“, gelegentlich auch „Plausibilität“), woraus eine neue, verbesserte Erkenntnis (A-posteriori-Wahrscheinlichkeitsverteilung) resultiert. Die A-posteriori-Wahrscheinlichkeitsverteilung eignet sich als neuer Prior, wenn neue Daten zur Verfügung stehen.
Struktur bayesscher Verfahren[Bearbeiten | Quelltext bearbeiten]
Die Verwendung des Satzes von Bayes führt zu einer charakteristischen Struktur bayesscher Verfahren. Ein Modell soll mit einem Datensatz untersucht werden. Die Ausgangsfragestellung ist, wie die Wahrscheinlichkeiten für die Modellparameter verteilt sind, sofern die Daten und Vorwissen gegeben sind. Es soll also ein Ausdruck für gefunden werden.
Die einzelnen Wahrscheinlichkeiten haben eine feste Bezeichnung.
- A-priori-Wahrscheinlichkeit, also die Wahrscheinlichkeitsverteilung für gegeben das Vorwissen (ohne die Messdaten aus dem Versuch einzubeziehen)
- A-posteriori-Wahrscheinlichkeit, die Wahrscheinlichkeitsverteilung für gegeben das Vorwissen und die Messdaten
- Likelihood, auch inverse Wahrscheinlichkeit oder „Plausibilität“, die Wahrscheinlichkeitsverteilung für die Messdaten , wenn der Modellparameter und das Vorwissen gegeben sind.
- Evidenz, kann als Normierungsfaktor bestimmt werden.
Der Satz von Bayes führt direkt auf einen wichtigen Aspekt der bayesschen Statistik: Mit dem Parameter geht Vorwissen über den Ausgang des Experiments als Prior in die Auswertung mit ein. Nach dem Experiment wird aus Vorwissen und Messdaten eine Posteriorverteilung berechnet, die neue Erkenntnisse enthält. Für folgende Experimente wird dann der Posterior des ersten Experimentes als neuer Prior verwendet, der ein erweitertes Vorwissen hat, also .
Die folgende Abbildung zeigt links einen Prior mit Vorwissen: ist um 0,5 verteilt, jedoch ist die Verteilung sehr breit. Mit binomialverteilten Messdaten (Mitte) wird nun die Verteilung um genauer bestimmt, sodass eine schmalere, spitzere Verteilung als Posterior (rechts) abgeleitet werden kann. Bei weiteren Beobachtungen kann dieser Posterior wieder als Prior dienen. Entsprechen die Messdaten den bisherigen Erwartungen kann die Breite der Wahrscheinlichkeitsdichtefunktion weiter abnehmen, bei vom Vorwissen abweichenden Messdaten würde die Varianz der Verteilung wieder größer werden und der Erwartungswert würde sich gegebenenfalls verschieben.
Der bayessche Wahrscheinlichkeitsbegriff[Bearbeiten | Quelltext bearbeiten]
Der bayessche Wahrscheinlichkeitsbegriff definiert Wahrscheinlichkeiten als „Grad vernünftiger Erwartung“[4], also als Maß für die Glaubwürdigkeit einer Aussage, der von 0 (falsch, unglaubwürdig) bis 1 (glaubwürdig, wahr) reicht. Diese Interpretation von Wahrscheinlichkeiten und Statistik unterscheidet sich fundamental von der Betrachtung in der konventionellen Statistik, in der unendlich oft wiederholbare Zufallsexperimente unter dem Gesichtspunkt betrachtet werden, ob eine Hypothese wahr oder falsch ist.
Bayessche Wahrscheinlichkeiten beziehen sich auf eine Aussage . In der klassischen Logik können Aussagen entweder wahr (oft mit Wert 1 wiedergegeben) oder falsch (Wert 0) sein. Der bayessche Wahrscheinlichkeitsbegriff erlaubt nun Zwischenstufen zwischen den Extremen, eine Wahrscheinlichkeit von 0,25 gibt beispielsweise wieder, dass eine Tendenz besteht, dass die Aussage falsch sein könnte, aber keine Gewissheit besteht. Zudem ist es möglich, ähnlich der klassischen Aussagenlogik, aus elementaren Wahrscheinlichkeiten und Aussagen komplexere Wahrscheinlichkeiten zu bestimmen. Damit ermöglicht die bayessche Statistik Schlussfolgerungen und die Behandlung von komplexen Fragestellungen.
- gemeinsame Wahrscheinlichkeiten , also: Wie wahrscheinlich ist es, dass sowohl als auch wahr ist? Wie wahrscheinlich ist es beispielsweise über den gesamten Wetterzeitraum, dass gleichzeitig die Sonne scheint () und Regen fällt ().
- bedingte Wahrscheinlichkeiten , also: Wie wahrscheinlich ist es, dass wahr ist, wenn gegeben ist, dass wahr ist. Wie wahrscheinlich ist es beispielsweise über den Zeitraum des Regens (), dass gleichzeitig auch die Sonne scheint ().
Bayessche Inferenz am Beispiel des Münzwurfes[Bearbeiten | Quelltext bearbeiten]
Der Münzwurf ist ein klassisches Beispiel der Wahrscheinlichkeitsrechnung und eignet sich sehr gut, um die Eigenschaften der bayesschen Statistik zu erläutern. Betrachtet wird, ob beim Wurf einer Münze „Kopf“ (1) oder Nicht-Kopf (0, also „Zahl“) eintrifft. Typischerweise wird im Alltag oft angenommen, dass bei einem Münzwurf eine 50%ige Wahrscheinlichkeit besteht, eine bestimmte Seite oben auf zu finden: . Diese Annahme ist jedoch für eine Münze, die große Unebenheiten aufweist oder vielleicht sogar manipuliert ist, nicht sinnvoll. Die Wahrscheinlichkeit von 50 % wird deshalb im Folgenden nicht als gegeben angenommen, sondern durch den variablen Parameter ersetzt.
Mit dem bayesschen Ansatz kann untersucht werden, wie wahrscheinlich beliebige Werte für sind, also wie ausgewogen die Münze ist. Mathematisch entspricht dies der Suche nach einer Wahrscheinlichkeitsverteilung für , wobei Beobachtungen (Anzahl von Kopfwürfen und Zahlwürfen in einem Experiment mit Münzwürfen) berücksichtigt werden sollen: . Mit dem bayesschen Satz lässt sich diese Wahrscheinlichkeitsfunktion durch Likelihood und A-priori-Verteilung ausdrücken:
Die Likelihood ist hier eine Wahrscheinlichkeitsverteilung über die Anzahl der Kopfwürfe bei einer gegebenen Balance der Münze und einer gegebenen Anzahl an Würfen insgesamt . Diese Wahrscheinlichkeitsverteilung ist bekannt als Binomialverteilung
- .
Im Gegensatz zur A-posteriori-Verteilung ist in der Likelihood-Verteilung nur ein Parameter, der die Form der Verteilung bestimmt.
Zur Bestimmung der A-posteriori-Verteilung fehlt nun noch die A-priori–Verteilung. Auch hier muss – wie bei der Likelihood – eine geeignete Verteilungsfunktion für das Problem gefunden werden. Bei einer Binomialverteilung als Likelihood eignet sich eine Betaverteilung als A-priori-Verteilung (wegen der Binomial-Terme ).
- .
Die Parameter der Betaverteilung werden am Ende der Herleitung des Posteriors anschaulich verständlich werden. Zusammenfassen des Produktes aus Likelihood-Verteilung und Beta-Prior zusammen liefert als Ergebnis eine (neue) Betaverteilung als Posterior.
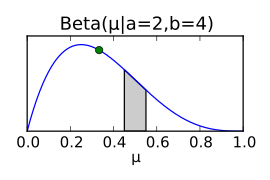
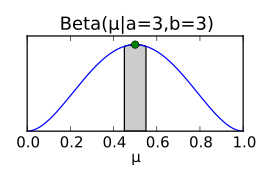
Somit ergibt sich aus dem bayesschen Ansatz, dass die A-posteriori-Verteilung des Parameters als Beta-Verteilung ausgedrückt werden kann, deren Parameter sich direkt aus den Parametern der A-priori–Verteilung und den gewonnenen Messdaten (Anzahl der Kopf-Würfe) gewinnen lässt. Diese A-posteriori-Verteilung kann wieder als Prior für ein Update der Wahrscheinlichkeitsverteilung verwendet werden, wenn etwa durch weitere Münzwürfe mehr Daten zur Verfügung stehen. In der folgenden Abbildung werden die Posteriorverteilungen für simulierte Münzwurf-Daten für jeden Münzwurf neu geplottet. Aus der Grafik geht hervor, wie sich die Posterior-Verteilung dem Simulationsparameter µ=0,35 (repräsentiert durch den grünen Punkt) mit steigender Anzahl der Würfe immer weiter annähert. Interessant ist hier insbesondere das Verhalten des Erwartungswerts der Posterior-Verteilung (blauer Punkt), da der Erwartungswert der Beta-Verteilung nicht notwendigerweise dem höchsten Punkt der Betaverteilung entspricht.
Die Wahrscheinlichkeitsverteilung über erlaubt – ganz im bayesschen Sinne – neben der Angabe des wahrscheinlichsten Wertes für auch eine Angabe der Genauigkeit von angesichts der gegebenen Daten.
Wahl des Priors[Bearbeiten | Quelltext bearbeiten]
Die Wahl der A-priori–Verteilung ist keineswegs beliebig. Im oberen Fall wurde eine A-priori-Verteilung – der konjugierte Prior – gewählt, welche mathematisch praktisch ist. Die Verteilung ist eine Verteilung, bei der jedes gleich wahrscheinlich ist. Diese Betaverteilung entspricht also dem Fall, dass kein nennenswertes Vorwissen über vorliegt. Nach wenigen Beobachtungen kann aus dem gleichförmigen Prior schon eine Wahrscheinlichkeitsverteilung werden, die die Lage von wesentlich genauer beschreibt, etwa .
Der Prior kann auch „Expertenwissen“ enthalten. Etwa kann bei einer Münze davon ausgegangen werden, dass in der Nähe von 50 % liegt, Werte in den Randbereichen (um 100 % und 0 %) dagegen unwahrscheinlich sind. Mit diesem Wissen lässt sich die Wahl eines Priors mit dem Erwartungswert 0,5 rechtfertigen. Diese Wahl wäre in einem anderen Fall, etwa der Verteilung von roten und schwarzen Kugeln in einer Urne vielleicht nicht angebracht, etwa wenn nicht bekannt ist, wie das Mischverhältnis ist oder ob sich überhaupt beide Farben in der Urne befinden.
Der Jeffreys’ Prior ist ein sogenannter nicht-informativer Prior (bzw. viel eher ein Verfahren, um einen nicht-informativen Prior zu bestimmen). Der Grundgedanke für den Jeffreys Prior ist, dass ein Verfahren zur Prior-Wahl, was ohne Vorkenntnis von Daten stattfindet, nicht von der Parametrisierung abhängen sollte. Für einen Bernoulli-Prozess ist der Jeffreys Prior .
Auch andere Prior-Verteilungen sind denkbar und können angesetzt werden. Teilweise wird dann jedoch die Bestimmung der Posteriorverteilung schwierig und sie kann oft nur numerisch bewältigt werden.
Konjugierte Prioren existieren für alle Mitglieder der Exponentialfamilie.
Unterschiede und Gemeinsamkeiten zu nicht-bayesschen Verfahren[Bearbeiten | Quelltext bearbeiten]
Die meisten nicht-bayesschen Verfahren unterscheiden sich in zwei Punkten von bayesschen Verfahren. Zum einen räumen nicht-bayessche Verfahren dem Satz von Bayes keinen zentralen Stellenwert ein (verwenden ihn oft nicht), zum anderen bauen sie oft auf einem anderen Wahrscheinlichkeitsbegriff auf: dem frequentistischen Wahrscheinlichkeitsbegriff. In der frequentistischen Interpretation von Wahrscheinlichkeiten sind Wahrscheinlichkeiten Häufigkeitsverhältnisse unendlich oft wiederholbarer Experimente.
Je nach eingesetztem Verfahren wird keine Wahrscheinlichkeitsverteilung bestimmt, sondern lediglich Erwartungswerte und allenfalls Konfidenzintervalle. Diese Einschränkungen führen jedoch oft zu numerisch einfachen Rechenverfahren in frequentistischen bzw. Ad-hoc-Verfahren. Um ihre Ergebnisse zu validieren, stellen nicht-bayessche Verfahren umfangreiche Techniken zur Validierung zur Verfügung.
Maximum-Likelihood-Ansatz[Bearbeiten | Quelltext bearbeiten]
Der Maximum-Likelihood-Ansatz ist ein nicht-bayessches Standardverfahren der Statistik. Anders als in der bayesschen Statistik wird nicht der Satz von Bayes angewendet, um eine Posteriorverteilung des Modellparameters zu bestimmen, vielmehr wird der Modellparameter so variiert, dass die Likelihood-Funktion maximal wird.
Da im frequentistischen Bild nur die beobachteten Ereignisse Zufallsvariablen sind, wird beim Maximum-Likelihood-Ansatz die Likelihood nicht als Wahrscheinlichkeitsverteilung der Daten gegen den Modellparameter aufgefasst, sondern als Funktion . Das Ergebnis einer Maximum-Likelihood-Schätzung ist ein Schätzer , der am ehesten mit dem Erwartungswert der Posteriorverteilung beim bayesschen Ansatz vergleichbar ist.
Die Maximum-Likelihood-Methode steht nicht komplett im Widerspruch zur bayesschen Statistik. Mit der Kullback-Leibler-Divergenz kann gezeigt werden, dass Maximum-Likelihood-Methoden näherungsweise Modellparameter schätzen, die der tatsächlichen Verteilung entsprechen.
Beispiele[Bearbeiten | Quelltext bearbeiten]
Beispiel von Laplace[Bearbeiten | Quelltext bearbeiten]
| Bouvard (1814) | 3512,0 |
| NASA (2004) | 3499,1 |
| Abweichung: | |
Laplace hat den Satz von Bayes erneut abgeleitet und verwendet, um die Masse des Saturn und anderer Planeten einzugrenzen.
- A: Die Masse des Saturn liegt in einem bestimmten Intervall
- B: Daten von Observatorien über gegenseitige Störungen von Jupiter und Saturn
- C: Die Masse des Saturn darf nicht so klein sein, dass er seine Ringe verliert, und nicht so groß, dass er das Sonnensystem zerstört.
« Pour en donner quelques applications intéressantes, j’ai profité de l’immense travail que M. Bouvard vient de terminer sur les mouvemens de Jupiter et de Saturne, dont il a construit des tables très précises. Il a discuté avec le plus grand soin les oppositions et les quadratures de ces deux planètes, observées par Bradley et par les astronomes qui l’ont suivi jusqu’à ces dernières années ; il en a conclu les corrections des élémens de leur mouvement et leurs masses comparées à celle du Soleil, prise pour unité. Ses calculs lui donnent la masse de Saturne égale à la 3512e partie de celle du Soleil. En leur appliquant mes formules de probabilité, je trouve qu’il y a onze mille à parier contre un, que l’erreur de ce résultat n’est pas un centième de sa valeur, ou, ce qui revient à très peu près au même, qu’après un siècle de nouvelles observations ajoutées aux précédentes, et discutées de la même manière, le nouveau résultat ne différera pas d’un centième de celui de M. Bouvard. »
„Um einige interessante Anwendungen davon zu nennen, habe ich von der gewaltigen Arbeit profitiert, die M. Bouvard gerade über die Bewegungen von Jupiter und Saturn beendet und von denen er sehr präzise Tabellen erstellt hat. Er hat mit größter Sorgfalt die Oppositionen und Quadraturen dieser beiden Planeten diskutiert, die von Bradley und den Astronomen, die ihn in den letzten Jahren begleitet haben, beobachtet wurden; er schloss auf die Korrekturen der Elemente ihrer Bewegung und ihrer Massen im Vergleich zur Sonne, die als Referenz verwendet wurde. Seinen Berechnungen zufolge beträgt die Saturnmasse den 3512ten Teil der Sonnenmasse. Meine Formeln der Wahrscheinlichkeitsrechnung auf diese angewandt, komme ich zu dem Schluss, dass die Chancen 11 000 zu 1 stehen, dass der Fehler dieses Ergebnisses nicht ein Hundertstel seines Wertes ist, oder, was das Gleiche bedeutet, dass auch nach einem Jahrhundert mit neuen Beobachtungen, zusätzlich zu den bereits existierenden, das neue Ergebnis nicht mehr als ein Hundertstel von dem von M. Bouvard abweichen wird, sofern sie auf die gleiche Weise durchgeführt werden.“
Die Abweichung vom korrekten Wert betrug tatsächlich nur etwa 0,37 Prozent, also deutlich weniger als ein Hundertstel.
Siehe auch[Bearbeiten | Quelltext bearbeiten]
Literatur[Bearbeiten | Quelltext bearbeiten]
- Christopher M. Bishop: Pattern Recognition And Machine Learning. 2. Auflage. Springer, New York 2006, ISBN 0-387-31073-8.
- Leonhard Held: Methoden der statistischen Inferenz. Likelihood und Bayes. Spektrum Akademischer Verlag, Heidelberg 2008, ISBN 978-3-8274-1939-2.
- Rudolf Koch: Einführung in die Bayes-Statistik. Springer, Berlin/Heidelberg 2000, ISBN 3-540-66670-2.
- Peter M. Lee: Bayesian Statistics. An Introduction. 4. Auflage. Wiley, New York 2012, ISBN 978-1-118-33257-3.
- David J.C. MacKay: Information Theory, Inference and Learning Algorithms. Cambridge University Press, Cambridge 2003, ISBN 0-521-64298-1.
- Dieter Wickmann: Bayes-Statistik. Einsicht gewinnen und entscheiden bei Unsicherheit (= Mathematische Texte Band 4). Bibliographisches Institut Wissenschaftsverlag, Mannheim/Wien/Zürich 1991, ISBN 3-411-14671-0.
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Andrew Gelman, John B. Carlin, Hal S. Stern, David B. Dunson, Aki Vehtari, Donald B. Rubin: Bayesian data analysis (= Texts in statistical science series). Third edition Auflage. CRC Press, Taylor and Francis Group, Boca Raton London New York 2014, ISBN 978-1-4398-4095-5.
- ↑ Christopher M. Bishop: Pattern Recognition And Machine Learning. 2. Auflage. Springer, New York 2006, ISBN 978-0-387-31073-2.
- ↑ Heinz Holling, Günther Gediga: Statistik - Wahrscheinlichkeitstheorie und Schätzverfahren (= Bachelorstudium Psychologie). Hogrefe, Göttingen Bern Wien 2013, ISBN 978-3-8017-2135-0.
- ↑ R. T. Cox: Probability, Frequency and Reasonable Expectation. In: American Journal of Physics. Band 14, Nr. 1, 1946, S. 1–13, doi:10.1119/1.1990764.
- ↑ Pierre-Simon Laplace: Essai philosophique sur les probabilités. Dover 1840, Seite 91–134, digitale Volltext-Ausgabe bei Wikisource (französisch).