Box-Muller-Methode
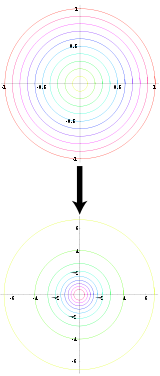
Die Box-Muller-Methode (nach George Edward Pelham Box und Mervin Edgar Muller 1958) ist ein Verfahren zur Erzeugung normalverteilter Zufallszahlen.
Definition[Bearbeiten | Quelltext bearbeiten]

Bei dieser Methode werden zunächst zwei unabhängige Standardzufallszahlen und benötigt. Diese lassen sich beispielsweise mit einem Zufallszahlengenerator erzeugen. Standardzufallszahlen unterliegen einer Rechteckverteilung mit den Parametern und .
Es lässt sich zeigen, dass man nach folgendem Transformationsschritt daraus zwei standardnormalverteilte (stochastisch) unabhängige Zufallszahlen und erhält:
und
- .
Schreibt man das Paar mit Polarkoordinaten, also
- und ,
dann gilt:
- und .
Anwendung der Inversionsmethode zur Transformation von und in die Polarkoordinaten und zeigt, dass einer Rechteckverteilung mit den Parametern und unterliegt und einer Exponentialverteilung mit dem Parameter . Aus diesem Ergebnis lässt sich die gemeinsame Verteilung von und herleiten. Sie beruht auf der Beziehung:
Die bisherigen Transformationsschritte erzeugen zwei standardnormalverteilte Zufallszahlen. Eine Standardnormalverteilung ist ein Spezialfall der Normalverteilung, nämlich mit dem Erwartungswert und der Varianz .
Um mit der Box-Muller-Methode Normalverteilungen mit beliebigen Parametern zu erzeugen, lassen sich die erhaltenen nach dem Muster
transformieren. In der obigen Notation steht wie üblich für die Kreiszahl, für den Sinus, für den Kosinus und für den natürlichen Logarithmus.
Verwendet man zur Erzeugung der einen linearen Kongruenzgenerator, so liegen die Paare auf einer durch eine Spirale beschriebenen Kurve. Dieses Verhalten ist eng mit dem im Satz von Marsaglia beschriebenen Hyperebenenverhalten linearer Kongruenzgeneratoren verwandt.
Dieses Problem lässt sich umgehen, wenn statt des linearen Kongruenzgenerators ein inverser Kongruenzgenerator oder die Polar-Methode verwendet wird.
Die Box-Muller-Methode erzeugt zunächst zwei stochastisch unabhängige und standardnormalverteilte Zufallszahlen, die sich dann in eine Normalverteilung mit beliebigen Parametern transformieren lassen. Die Box-Muller-Methode erfordert die Auswertung von Logarithmen und trigonometrischen Funktionen, was auf einigen Rechnern sehr zeitaufwendig sein kann.
Weitere Möglichkeiten zur Erzeugung normalverteilter Zufallszahlen sind im Artikel Normalverteilung beschrieben. Eine Alternative ist z. B. die Polar-Methode.[1]
Programmierung[Bearbeiten | Quelltext bearbeiten]
Die Standard-Box-Muller-Methode erzeugt Werte aus der Standardnormalverteilung mit Erwartungswert 0 und Standardabweichung 1. Die folgende Implementierung in der Programmiersprache C++ generiert 10 Paare von standardnormalverteilten Zufallszahlen aus jeder Normalverteilung mit Erwartungswert μ und Varianz σ und gibt sie auf der Konsole aus.
#define _USE_MATH_DEFINES
#include <random>
#include <iostream>
using namespace std;
// Diese Funktion berechnet zwei standardnormalverteilte Zufallszahlen z0 und z1
pair<double, double> generateGaussianNoise(double mu, double sigma)
{
constexpr double epsilon = numeric_limits<double>::epsilon();
// Initialisiert den Zufallszahlengenerator im Bereich von 0 bis 1
static mt19937 rng(random_device{}()); // Standard Mersenne-Twister
static uniform_real_distribution<> runif(0, 1);
double u1, u2; // Deklaration der lokalen Variablen für die Zufallszahlen u1 und u2
do // Diese do-while-Schleife erzeugt solange Zufallszahlen bis u1 > epsilon ist
{
u1 = runif(rng);
} while (u1 <= epsilon);
u2 = runif(rng);
// Berechnet z0 und z1
auto magnitude = sigma * sqrt(-2.0 * log(u1));
auto z0 = magnitude * cos(2.0 * M_PI * u2) + mu;
auto z1 = magnitude * sin(2.0 * M_PI * u2) + mu;
return make_pair(z0, z1);
}
// Hauptfunktion die das Programm ausführt
void main()
{
double mu = 0; // Deklaration der lokalen Variablen
double sigma = 1;
for (int i = 0; i < 10; i++) // Diese for-Schleife berechnet 10 Paare von standardnormalverteilte Zufallszahlen und gibt sie auf der Konsole aus
{
pair<double, double> gaussianNoise = generateGaussianNoise(mu, sigma); // Aufruf der Funktion
cout << gaussianNoise.first << "," << gaussianNoise.second << endl; // Ausgabe auf der Konsole
}
}
Literatur[Bearbeiten | Quelltext bearbeiten]
- George Edward Pelham Box, Mervin Edgar Muller: A note on the generation of random normal deviates. In: Annals of Mathematical Statistics, Jg. 29 (1958), Heft 2, ISSN 0003-4851, S. 610–611.
- Donald Ervin Knuth: The Art of Computer Programming, Sec. 3.4.1, S. 117.
- Otto Moeschlin, Eugen Grycko, Claudia Pohl, Frank Steinert: Kapitel 1.4 Generating Sample Values. In: Diess.: Experimental Stochastics. Springer, Berlin u. a. 1998, ISBN 3-540-14619-9.
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Vgl. Albert J. Kinderman und John G. Ramage: Computer Generation of Normal Random Numbers. In: Journal of the American Statistical Association, Jg. 71 (1976), Heft 356, S. 893–896.




























