Hyperebene
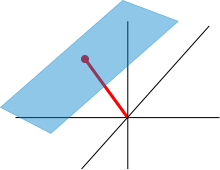
Eine Hyperebene ist in der Mathematik eine Verallgemeinerung des Begriffs der Ebene vom Anschauungsraum auf Räume beliebiger Dimension. Ähnlich wie eine Ebene im dreidimensionalen Raum durch einen Stützvektor und zwei Richtungsvektoren beschrieben werden kann, wird eine Hyperebene im -dimensionalen Raum durch einen Stützvektor und Richtungsvektoren dargestellt. Im -dimensionalen Koordinatenraum ist eine Hyperebene die Lösungsmenge einer linearen Gleichung mit Unbekannten. Hyperebenen spielen daher eine wichtige Rolle bei der Lösungsstruktur linearer Gleichungs- und Ungleichungssysteme.
In der linearen Algebra werden Hyperebenen auch in unendlichdimensionalen Vektorräumen betrachtet und sind dort gerade die affinen Unterräume mit Kodimension eins. Jede Hyperebene entsteht durch Verschiebung eines Untervektorraums um einen festen Vektor. Kann dabei der Nullvektor gewählt werden, spricht man auch von einer linearen Hyperebene, da dann die Hyperebene selbst einen Vektorraum darstellt. Zur besseren Unterscheidung spricht man im Fall eines beliebigen Verschiebungsvektors auch von einer affinen Hyperebene.
Jeder Untervektorraum mit Kodimension eins kann auch als Kern eines linearen Funktionals charakterisiert werden. In der Funktionalanalysis werden insbesondere abgeschlossene Hyperebenen betrachtet, die durch stetige lineare Funktionale beschrieben werden. In der projektiven Geometrie werden auch projektive Hyperebenen als projektive Teilräume mit Kodimension eins untersucht. Einen noch weiter verallgemeinerten Hyperebenenbegriff findet man in der Matroidtheorie.
Euklidische Geometrie[Bearbeiten | Quelltext bearbeiten]
Definition[Bearbeiten | Quelltext bearbeiten]

Eine Hyperebene im -dimensionalen euklidischen Raum ist eine Teilmenge der Form
- ,
wobei ein Stützvektor der Hyperebene ist und linear unabhängige Richtungsvektoren der Hyperebene sind.[1] Die Richtungsvektoren spannen dabei ein affines Koordinatensystem auf, wobei die affinen Koordinaten eines Punkts der Hyperebene sind.
Beispiele[Bearbeiten | Quelltext bearbeiten]
- Im eindimensionalen euklidischen Raum stellt jeder Punkt eine Hyperebene dar.
- Im zweidimensionalen euklidischen Raum stellt jede Gerade eine Hyperebene dar.
- Im dreidimensionalen euklidischen Raum stellt jede Ebene eine Hyperebene dar.
Weitere Darstellungen[Bearbeiten | Quelltext bearbeiten]
Neben der obigen Parameterform gibt es noch weitere Darstellungsformen für Hyperebenen. In Normalenform lautet die Darstellung einer Hyperebene
- ,
wobei ein Normalenvektor der Hyperebene ist, wieder ein Stützvektor der Hyperebene ist und das Standardskalarprodukt zweier Vektoren bezeichnet.[2] In hessescher Normalform hat eine Hyperebene die entsprechende Darstellung
- ,
wobei ein normierter und orientierter Normalenvektor der Hyperebene ist und den Abstand der Hyperebene vom Koordinatenursprung beschreibt.[2] Die hessesche Normalform erlaubt eine effiziente Berechnung des Abstands eines beliebigen Punkts des Raums von der Hyperebene.
In Koordinatenform lautet die Darstellung einer Hyperebene
- ,
wobei sind und mindestens einer der Koeffizienten ungleich null ist.[3] Die Koordinatenform ergibt sich aus der Normalenform durch Ausmultiplizieren, wobei und gesetzt werden.
Verwendung[Bearbeiten | Quelltext bearbeiten]

Wie aus der Koordinatenform ersichtlich, stellt die Lösungsmenge einer linearen Gleichung mit Unbekannten der Form
eine Hyperebene im -dimensionalen euklidischen Raum dar. Jede Zeile eines linearen Gleichungssystems beschreibt daher eine solche Hyperebene. Die Lösungsmenge des linearen Gleichungssystems ist dann der Schnitt aller dieser Hyperebenen.[3] Entsprechend dazu beschreibt die Lösungsmenge einer linearen Ungleichung der Form
einen Halbraum im -dimensionalen euklidischen Raum, der von einer Hyperebene begrenzt wird. Die Lösungsmenge eines linearen Ungleichungssystems ist dann der Schnitt solcher Halbräume und stellt damit ein konvexes Polytop dar, beispielsweise einen Hyperwürfel, ein Hyperrechteck oder einen Simplex (Hypertetraeder). Die lineare Optimierung beschäftigt sich mit Verfahren zur Maximierung einer vorgegebenen linearen Zielfunktion in einem konvexen Polytop.[4]
Eine Hyperebene heißt Stützhyperebene einer gegebenen Menge im euklidischen Raum, wenn sie den Rand der Menge schneidet und die Menge vollständig in einem der beiden durch die Hyperebene definierten abgeschlossenen Halbräume liegt. Ist die Menge konvex, dann existiert für jeden Randpunkt der Menge eine solche Stützhyperebene.[5]
Nach dem Satz von Stone-Tukey (englisch Ham sandwich theorem) können beschränkte messbare Mengen im -dimensionalen euklidischen Raum durch eine Hyperebene gleichzeitig jeweils halbiert werden.
Lineare Algebra[Bearbeiten | Quelltext bearbeiten]
In der linearen Algebra wird das Konzept der Hyperebene auf Vektorräume über beliebigen Körpern und beliebiger Dimension verallgemeinert.
Definition[Bearbeiten | Quelltext bearbeiten]
Ist ein Vektorraum über dem Körper , dann ist eine Hyperebene eine Teilmenge der Form
- ,
wobei ein beliebiger Vektor und ein Untervektorraum von mit Kodimension ist. Hyperebenen sind demnach maximale echte affine Unterräume, das heißt, jeder echte affine Unterraum ist in einer Hyperebene enthalten. Eine Hyperebene wird als lineare Hyperebene bezeichnet, wenn sie den Nullvektor enthält, das heißt, wenn in der Definition gewählt werden kann.
Beispiele[Bearbeiten | Quelltext bearbeiten]
In den folgenden Beispielen sei ein Körper der Charakteristik , beispielsweise die reellen oder komplexen Zahlen.
- Im Koordinatenraum stellen die Koordinatenvektoren, die eine lineare Gleichung der Form erfüllen, eine Hyperebene dar. Ist , handelt es sich dabei um eine lineare Hyperebene.
- Im Matrizenraum stellen die Matrizen, bei denen die Summe aller Einträge konstant ist, eine Hyperebene dar. Ist diese Konstante , handelt es sich dabei um eine lineare Hyperebene.
- Im Polynomraum stellen die Polynome der Form , wobei fest vorgegeben ist, eine Hyperebene dar. Im Fall handelt es sich dabei um eine lineare Hyperebene.
- Im Funktionenraum stellen die Funktionen mit für ein festes und eine Hyperebene dar. Im Fall handelt es sich dabei um eine lineare Hyperebene.
Weitere Darstellungen[Bearbeiten | Quelltext bearbeiten]
Nachdem jeder Untervektorraum der Kodimension auch als Kern eines linearen Funktionals , das nicht das Nullfunktional ist, charakterisiert werden kann, hat eine Hyperebene die Darstellung[6]
- .
Durch Setzen von ergibt sich daraus dann die äquivalente Darstellung[6]
- .
Hierbei sind und für eine gegebene Hyperebene nur bis auf einen gemeinsamen Faktor eindeutig bestimmt. Umgekehrt stellt das Urbild für jedes lineare Funktional , das ungleich dem Nullfunktional ist, und für jeden Skalar eine Hyperebene dar.[6]
Diese Aussagen bleiben auch dann noch gültig, wenn ein Schiefkörper und ein Linksvektorraum über ist.
Verwendung[Bearbeiten | Quelltext bearbeiten]
In der Funktionalanalysis betrachtet man unendlichdimensionale Vektorräume über oder , auf denen eine Topologie erklärt ist, die sie zu topologischen Vektorräumen macht. Hier interessiert man sich besonders für Hyperebenen, die durch stetige lineare Funktionale definiert sind. Da ein lineares Funktional genau dann stetig ist, wenn sein Kern abgeschlossen ist,[7] definieren die stetigen linearen Funktionale ungleich dem Nullfunktional genau die abgeschlossenen Hyperebenen. Für normierte Räume, allgemeiner lokalkonvexe Räume, gibt es nach dem Satz von Hahn-Banach sehr viele solcher stetigen linearen Funktionale und damit auch abgeschlossene Hyperebenen der Form
mit . Diese Reichhaltigkeit schlägt sich im Trennungssatz nieder, nach dem zwei disjunkte konvexe, kompakte Mengen durch eine solche abgeschlossene Hyperebene getrennt werden können.
Die Trennungseigenschaft lässt sich auch für affine Räume über angeordneten Körpern mit dem Konzept der (starken) Seiteneinteilung verallgemeinern. Auch für nichtdesarguessche affine Ebenen existiert in gewissen Fällen eine (schwache) Seiteneinteilung durch Geraden.
Projektive Geometrie[Bearbeiten | Quelltext bearbeiten]
Definition[Bearbeiten | Quelltext bearbeiten]
Ist der projektive Raum zu dem Vektorraum , dann ist eine (projektive) Hyperebene eine Teilmenge der Form
- ,
wobei ein Untervektorraum von der Kodimension eins ist und die Äquivalenzrelation skalare Vielfache von Vektoren ungleich dem Nullvektor miteinander identifiziert. Die Hyperebenen in sind demnach gerade die projektiven Unterräume der Kodimension eins. Eine projektive Hyperebene stellt selbst wieder einen projektiven Raum dar, nämlich gerade den Raum . Ist -dimensional, dann ist -dimensional und -dimensional.
Beispiele[Bearbeiten | Quelltext bearbeiten]
Ist der zugrunde liegende Vektorraum der euklidische Raum , dann gibt es folgende Entsprechungen:
- Eine Hyperebene (ein Punkt) auf der projektiven Geraden entspricht einer Ursprungsgerade in der euklidischen Ebene .
- Eine Hyperebene (eine Gerade) in der projektiven Ebene entspricht einer Ursprungsebene im euklidischen Raum .
- Eine Hyperebene (eine Ebene) im projektiven Raum entspricht einer Ursprungshyperebene im euklidischen Raum .
Koordinatendarstellung[Bearbeiten | Quelltext bearbeiten]

Sind die homogenen Koordinaten eines Punkts im -dimensionalen projektiven Standardraum , dann hat eine projektive Hyperebene die Koordinatendarstellung
- ,
wobei sind und mindestens einer der Koeffizienten ungleich null ist.
Eine nichtdesarguessche projektive Ebene lässt sich jedoch nicht auf diese Weise koordinatisieren. Dort sind die Hyperebenen per Definition die Geraden.
Bezug zu affinen Räumen[Bearbeiten | Quelltext bearbeiten]
Ist eine Hyperebene in einem projektiven Raum , dann stellt die Menge
einen affinen Raum dar, wobei eine entsprechende Einbettung von in ist. Der Translationsraum von ist dabei gerade der zu zugehörige Untervektorraum . Die Punkte von heißen dann eigentlich, die Punkte von uneigentlich oder Fernpunkte. Umgekehrt lässt sich jeder affine Raum durch disjunkte Vereinigung mit einer Fernhyperebene gleicher Dimension zu einem projektiven Raum
erweitern. Ist beispielsweise und , dann ist die zugehörige Einbettung mit der Inversen .
Verwendung[Bearbeiten | Quelltext bearbeiten]
Eine Anwendung projektiver Hyperebenen in der algebraischen Geometrie und der algebraischen Topologie bietet der Satz von Lefschetz über Hyperebenenschnitte, der einen Zusammenhang zwischen der Gestalt einer komplexen projektiven Varietät und der Gestalt ihrer Untervarietäten herstellt.
In der endlichen Geometrie haben unter den endlichen affinen oder projektiven Geometrien diejenigen besondere Eigenschaften, bei denen – neben den gewöhnlichen Punkten als Punktmenge – speziell die Hyperebenen des Raumes als Blockmenge gewählt werden.
Siehe auch[Bearbeiten | Quelltext bearbeiten]
- Hyperfläche, eine Verallgemeinerung von Hyperebenen auf gekrümmte Mannigfaltigkeiten
- Householdertransformation, die Spiegelung eines Vektors an einer Hyperebene
Literatur[Bearbeiten | Quelltext bearbeiten]
Reelle Geometrie und Funktionalanalysis
- Hans Wilhelm Alt: Lineare Funktionalanalysis. Eine anwendungsorientierte Einführung. 5. Auflage. Springer, Berlin 2006, ISBN 3-540-34186-2.
- Harro Heuser: Lehrbuch der Analysis. Band I und II. Teubner, Wiesbaden 2003, ISBN 3-519-62233-5.
- Harro Heuser: Funktionalanalysis. Theorie und Anwendung. 3. Auflage. Teubner, Wiesbaden 1992, ISBN 3-519-22206-X.
Lineare Algebra und analytische Geometrie
- Hermann Schaal: Lineare Algebra und analytische Geometrie, Band I und II. 2. durchgesehene Auflage. Vieweg, Braunschweig 1980, ISBN 3-528-13057-1.
- Günter Scheja, Uwe Storch: Lehrbuch der Algebra: unter Einschluß der linearen Algebra. 2., überarb. und erw. Auflage. Teubner, Stuttgart 1994, ISBN 3-519-12203-0.
- Uwe Storch, Hartmut Wiebe: Lehrbuch der Mathematik für Mathematiker, Informatiker und Physiker. Band II: Lineare Algebra. BI-Wissenschafts-Verlag, 1990, ISBN 3-411-14101-8.
Anwendungen in der Geometrie (Seiteneinteilung)
- Wendelin Degen und Lothar Profke: Grundlagen der affinen und euklidischen Geometrie. Teubner, Stuttgart 1976, ISBN 3-519-02751-8.
- Emanuel Sperner: Die Ordnungsfunktionen einer Geometrie. In: Math. Ann. Band 121. Teubner, 1949, S. 107–130.
Weblinks[Bearbeiten | Quelltext bearbeiten]
- M. I. Voitsekhovskii: Hyperplane. In: Michiel Hazewinkel (Hrsg.): Encyclopedia of Mathematics. Springer-Verlag und EMS Press, Berlin 2002, ISBN 1-55608-010-7 (englisch, encyclopediaofmath.org).
- Eric W. Weisstein: Hyperplane. In: MathWorld (englisch).
- georgiosl: Hyperplane. In: PlanetMath. (englisch)
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Klemens Burg, Herbert Haf, Friedrich Wille, Andreas Meister: Höhere Mathematik für Ingenieure Band II: Lineare Algebra. Springer, 2012, ISBN 978-3-8348-2267-3, S. 81.
- ↑ a b Hermann Schichl, Roland Steinbauer: Einführung in das mathematische Arbeiten. Springer, 2012, ISBN 978-3-642-28646-9, S. 462.
- ↑ a b Peter Knabner, Wolf Barth: Lineare Algebra: Grundlagen und Anwendungen. Springer, 2012, ISBN 978-3-642-32186-3, S. 41–42.
- ↑ Rainer E. Burkard, Uwe T. Zimmermann: Einführung in die Mathematische Optimierung. Springer, 2012, ISBN 978-3-642-28673-5, S. 24.
- ↑ Rainer E. Burkard, Uwe T. Zimmermann: Einführung in die Mathematische Optimierung. Springer, 2012, ISBN 978-3-642-28673-5, S. 247.
- ↑ a b c Max Koecher: Lineare Algebra und analytische Geometrie. Springer, 2012, ISBN 978-3-642-96772-6, S. 167.
- ↑ R.V. Kadison, J. R. Ringrose: Fundamentals of the Theory of Operator Algebras, Volume I, Academic Press (1983), ISBN 0-12-393301-3, Korollar 1.2.5



































![{\displaystyle K[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5bb4d802ca5718a14dc961af8692f35cdfad169b)


















































