Feistelchiffre

Feistelchiffre, auch als Feistelnetzwerk bezeichnet, ist eine allgemeine Struktur, mit der Blockchiffren realisiert werden können. Ein Mitarbeiter von IBM, Horst Feistel, gilt als der Erfinder dieser Chiffre. Er arbeitete in den 1970er Jahren mit anderen am sog. Projekt „Lucifer“, dessen Ziel es war, eine effiziente Verschlüsselungstechnologie zu entwickeln. Die Feistelchiffre war später dann die Grundlage für den DES-Algorithmus.

Viele moderne symmetrische Verschlüsselungsalgorithmen basieren auf Feistelnetzwerken. Dies rührt daher, dass Blockverschlüsselungen, welche auf Feistelnetzwerken basieren, garantiert umkehrbar (bijektiv) sind. Damit ist die notwendige Grundbedingung für Blockchiffren erfüllt, dass es bei der Abbildung von Chiffreblöcken auf Klartextblöcke bei der Entschlüsselung zu keinen Mehrdeutigkeiten kommen darf. Weiterhin wurde diese Struktur von sehr vielen Kryptografen analysiert und für gut befunden.

Arbeitsweise

Struktur eines Feistelchiffre

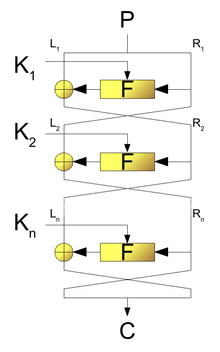
Wie es der Name „Blockchiffre“ schon nahelegt, wird der Klartext zuerst in einzelne Blöcke zerlegt. Die Größe dieser Blöcke hängt vom jeweiligen Verschlüsselungsverfahren ab, oft ist sie ein Vielfaches von 64 Bit. Jeder dieser Blöcke wird dann in zwei (meist gleichgroße) Teile ($L_1$ und $R_1$) geteilt und in $n$ Runden mit verschiedenen Rundenschlüsseln verschlüsselt. Nach den Runden werden die Teile wieder zusammengesetzt. Innerhalb der $i$-ten Runde ($i$ läuft von 1 bis $n$) wird folgende Formel angewendet:

$L_{i+1} \!\, = R_i$

$R_{i+1} \!\, = L_i \oplus F(R_i, K_i)$

Dabei bildet $F$ die sog. Runden- oder Transformationsfunktion und $K_1$ bis $K_n$ sind die Rundenschlüssel. $\oplus$ steht für eine einfach invertierbare Verknüpfung. Oft nimmt man dafür das bitweise XOR, das mit seiner Umkehrung identisch ist, häufig auch Addition oder Subtraktion modulo $2^e$, die zur Entschlüsselung gegeneinander ausgetauscht werden. $e$ ist dabei die Breite der Teile $L_i$ bzw. $R_i$. Der verschlüsselte Text am Ende der Runden ist die Zusammenführung $C = \left(L_{n+1},R_{n+1}\right)$.

Feistelnetzwerke ermöglichen eine Entschlüsselung, ohne dass die Umkehrfunktion von $F$ benötigt wird. Will man einen Geheimtext dechiffrieren, wendet man die Umkehrung der obigen Formel an, wobei man $i$ von $n$ bis 1 laufen lässt:

$R_i \!\, = L_{i+1}$

$L_i \!\, = R_{i+1}\ominus F(L_{i+1}, K_i)$

$\ominus$ ist dabei die Umkehrung zu $\oplus$.

Variante

Manche Verfahren verknüpfen auch die Rundenschlüssel direkt mit den Textteilen, und die Rundenfunktion $F$ ist dann (meist) nicht vom Schlüssel abhängig:

$L_{i+1} \!\, = R_i \circ K_i$

$R_{i+1} \!\, = L_i \oplus F(L_{i+1})$

$\oplus$ und $\circ$ stehen wiederum für (nicht unbedingt verschiedene) einfach invertierbare Verknüpfungen.

Interner Zustand

Ein balanciertes Feistelnetzwerk (BFN) liegt dann vor, wenn die beiden Hälften, die in die Rundenfunktion eingehen, gleich groß sind. Von einem unbalancierten (nicht-balancierten) Feistelnetzwerk (UFN) spricht man, wenn entweder die beiden Hälften nicht gleich groß sind oder aus einem Block für die Rundenfunktion mehr als zwei Teile gebildet werden.

Anwendungen

Feistelnetzwerke kommen u. a. in folgenden Chiffren zum Tragen:

• Blowfish
• CAST
• DES/Triple-DES
• FEAL
• MARS
• TEA/XTEA
• Twofish
• MISTY1

Weblinks

• Beispielprogramm zur Berechnung

Literatur

• Horst Feistel: Cryptography and Computer Privacy. In: Scientific American. 228, Nr. 5, Mai 1973, S. 15-23.