Gompertz-Funktion
Zur Navigation springen
Zur Suche springen
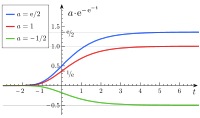
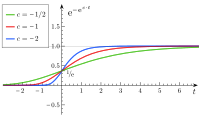
Die nach ihrem Entdecker, dem britischen Mathematiker Benjamin Gompertz, benannte Gompertz-Funktion ist eine asymmetrische Sättigungsfunktion, die sich im Gegensatz zur logistischen Funktion dadurch auszeichnet, dass sie sich ihrer rechten bzw. oberen Asymptote gemächlicher annähert als ihrer linken bzw. unteren, der Graph ihrer ersten Ableitung also ausgehend von deren Maximum bei nach rechts hin langsamer abfällt als nach links.
Die Funktion[Bearbeiten | Quelltext bearbeiten]
Die allgemeine Formel der Gompertz-Funktion lautet:
- ist die obere Asymptote, da wegen .
- ist die -Verschiebung
- ist das Steigungsmaß[1]
- ist die Eulersche Zahl ()
- e·b·c die Wachstumsrate[2]
Variationen der Variablen[Bearbeiten | Quelltext bearbeiten]
-
Variationen von
-
Variationen von
-
Variationen von
Anwendung[Bearbeiten | Quelltext bearbeiten]
Die Gompertz-Funktion findet in der Biologie (z. B. zur Beschreibung des Wachstums von Tumoren) und in den Wirtschaftswissenschaften (z. B. in der empirischen Trendforschung) Anwendung.[3]
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Gompertzfunktion, Wirtschaftslexikon24.com
- ↑ Kathleen M. C. Tjørve, Even Tjørve: The use of Gompertz models in growth analyses, and new Gompertz-model approach: An addition to the Unified-Richards family. In: PLOS ONE. Band 12, Nr. 6, 5. Juni 2017, ISSN 1932-6203, S. e0178691, doi:10.1371/journal.pone.0178691 (plos.org [abgerufen am 14. April 2021]).
- ↑ Gompertz-Funktion in der Funktionstypenbibliothek ( vom 13. September 2014 im Internet Archive)