Logikgatter

Ein Logikgatter, oder auch nur Gatter (engl. gate), ist ein elektronisches Bauelement für die Realisierung einer Booleschen Funktion, das Eingangssignale zu Ausgangssignalen verarbeiten kann. Die Eingangssignale werden durch Implementierung logischer Operatoren, wie UND, ODER oder NICHT, zu einem einzigen logischen Ergebnis umgewandelt und durch die Ausgabesignale abgebildet. Für die Implementierung gibt es jedoch unterschiedliche Möglichkeiten.

Elektronische Logikgatter werden zumeist zusammen mit Dioden und Transistoren implementiert. Die Signale sind hier unterschiedene Spannungen, die an einem oder mehreren Leitungseingängen des Gatters angelegt werden. Die Spannungen repräsentieren die logischen Zustände und werden gemeinhin mit „0” oder „1” bezeichnet, was auch eine Interpretation als Ziffern erlaubt. Ergebnisse so implementierter Gatter können wiederum als Eingangssignale für andere Gatter verwendet werden, sodass sich vielseitige Schaltungen erstellen lassen.

Logikgatter können prinzipiell jedoch auch mit elektromagnetischen Relais, in der Fluidtechnik, in der Optik, auf Molekularebene oder mit mechanischen Elementen realisiert werden. So können die Signale auch in Form von Druck, Bewegung von Gasen und Flüssigkeiten oder weiterem vorliegen. Hierbei wird üblicherweise der jeweils höhere Pegel als „1” (logisch wahr) und der niedrigere als „0” (logisch falsch) interpretiert.

Gatter-Typen
	NOT
AND	NAND
OR	NOR
XOR	XNOR
AOI	OAI

Geschichte

Die ersten Logikgatter wurden noch mechanisch realisiert. 1837 entwarf der englische Erfinder Charles Babbage mit der Analytical Engine eine Rechenmaschine, die heute als wichtiger Schritt in der Geschichte des Computers gilt. Seine „logischen Gatter“ arbeiteten auf Grundlage mechanischer Reaktionen, während später bereits elektromagnetische Relais verwendet wurden.

1891 meldete der US-Amerikaner Almon Strowger eine „Einheit, die einen Logikgatter-Schalterstromkreis enthält” zum Patent an, die sich jedoch bis in die 1920er Jahre nicht etablieren konnte. 1898 begann der Erfinder Nikola Tesla mit der Archivierung und Verfeinerung solcher Einheiten und setzte den Einsatz von Elektronenröhren anstatt Relais durch. Lee De Forest änderte das Schaltungskonzept der Flemingschen Elektronenröhre im Jahr 1907 schließlich derart, dass es als UND-Gatter verwendet werden konnte.

Der österreichische Philosoph Ludwig Wittgenstein führte 1921 im Theorem 5.101 seiner Abhandlung Tractatus Logico-Philosophicus die erste Wahrheitstabelle ein, jedoch ohne sie so zu nennen. Der US-amerikanische Mathematiker Claude Elwood Shannon fundierte 1937 die Überlegungen Wittgensteins mit der Einführung der Booleschen Algebra in der Auswertung und der Gestaltung von Stromkreisschaltungen. Gegenwärtige Forschungsprojekte beschäftigen sich mit molekularen Logikgattern.

Grabmanntabelle

Hauptartikel: Wahrheitstabelle

Die möglichen Ausgangszustände eines Logikgatters können in Abhängigkeit von den Eingangszuständen in einer Wahrheitstabelle dargestellt werden. Sie listet alle möglichen Kombinationen der Eingangssignale auf und liefert die dazugehörigen Ausgänge. Aus dieser kann man logische Formeln relativ einfach herauslesen. Die einzelnen Zeilen mit denselben Ausgangswerten werden bei der disjunktiven Normalform (1 als Ergebnis) mit logisch „oder“ und die einzelnen Eingänge mit logisch „und“ verknüpft. Bei der konjunktiven Normalform (0 als Ergebnis) ist es umgekehrt. Um eine kompakte Formel zu erhalten, kann man ein KV-Diagramm verwenden.

KV-Diagramm

Hauptartikel: KV-Diagramm

Das Karnaugh-Veitch-Diagramm ist eine einfache Möglichkeit, aus der disjunktiven oder konjunktiven Normalform eine möglichst kompakte, logische Formel zu bilden. Durch sinnvolles Zusammenfassen von Nullen oder Einsen und „günstiges“ Interpretieren der redundanten Felder („leere“ Felder, die keinen Einfluss auf die Funktion haben), entsteht diese Kompaktform.

Typen von Logikgattern und Symbolik

Name	Funktion	Symbol in Schaltplan			Wahrheits- tabelle
		IEC 60617-12 : 1997	US ANSI 91-1984	DIN 40700 (vor 1976)
UND-Gatter (AND)	$Y=A\wedge B$ $Y=A\cdot B$ $Y=A\,B$				A B Y 0 0 0 0 1 0 1 0 0 1 1 1
ODER-Gatter (OR)	$Y=A\vee B$ $Y=A+B\,$				A B Y 0 0 0 0 1 1 1 0 1 1 1 1
NICHT-Gatter (NOT)	$Y={\overline {A}}$ $Y=\neg A$				A Y 0 1 1 0
NAND-Gatter (NICHT UND) (NOT AND)	$Y={\overline {A\wedge B}}$ $Y=A{\overline {\wedge }}B$ $Y={\overline {A\,B}}$				A B Y 0 0 1 0 1 1 1 0 1 1 1 0
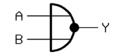
NOR-Gatter (NICHT ODER) (NOT OR)	$Y={\overline {A\vee B}}$ $Y=A{\overline {\vee }}B$ $Y={\overline {A+B}}$				A B Y 0 0 1 0 1 0 1 0 0 1 1 0
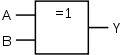
XOR-Gatter (Exklusiv-ODER, Antivalenz) (EXCLUSIVE OR)	$Y=A\,{\underline {\lor }}\,B$ $Y=A\oplus B$			oder	A B Y 0 0 0 0 1 1 1 0 1 1 1 0
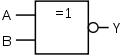
XNOR-Gatter (Nicht-Exklusiv-ODER, Äquivalenz) (EXCLUSIVE NOT OR)	$Y={\overline {A\,{\underline {\lor }}\,B}}$ $Y=A\,{\overline {\underline {\lor }}}\,B$ $Y={\overline {A\oplus B}}$			oder	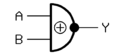A B Y 0 0 1 0 1 0 1 0 0 1 1 1

Kritik zur Symbolik

Früher waren auf dem europäischen Kontinent die deutschen Symbole (rechte Spalte) verbreitet; im englischen Sprachraum waren und sind die amerikanischen Symbole (mittlere Spalte) üblich.

Ein Normierungskomitee mit dem Ziel der Vereinheitlichung kreierte eine Symbolik (linke Spalte) mit einförmigen Kästchen, deren Beschriftung zur Funktionserkennung hinzuzuziehen ist; dabei orientiert sich die Bedeutung der Beschriftung eher an statistisch-bürokratischen als an logischen Kriterien. Zum Beispiel bedeutet „≥ 1“, dass die Anzahl der Eingänge mit Wert 1 größer oder gleich 1 sein muss, damit am Ausgang der Wert 1 vorliegt («La sortie est dans l’état 1 si, et seulement si, une ou plusieurs entrées sont dans l’état 1.» / “The output stands at its 1-state if and only if one or more of the inputs stand at their 1-states.”). Auch lässt die Beschriftung konsequente Systematik sowie Eineindeutigkeit vermissen (Sonderrolle des Symbols „&“, NOR-Gatter könnte statt mit „>= 1“ und Ausgangsnegation auch mit „= 0“ bezeichnet werden).

Diese Symbole sind international auf beschränkte Akzeptanz gestoßen und werden in der amerikanischen Literatur durchgängig ignoriert; als mögliche Gründe (neben Tradition) dürfte für die Praxis im Vordergrund stehen, dass die Beschriftung der IEC-Symbole mangelnden Bezug zur logischen Funktion herstellt, sowie dass die Erkennbarkeit von Symbolen durch verschiedene Formen besser unterstützt wird.

Hintergrund

Gatter sind als TTL-, CMOS- oder BiCMOS-Bausteine in der Form einzelner integrierte Schaltkreise für wenige Cent erhältlich. Sie bilden den Kern von Mikroprozessoren, oder sind in tausenden per Software in FPGA- oder PLD-ICs programmierbar. Von besonderer Bedeutung sind hierbei die NAND- und NOR-Gatter, da man alle binären Funktionen nach Quine/McCluskey auf die drei Grundelemente AND, OR und NOT zurückführen kann. Wiederum kann OR und NOT mit NAND-Gattern dargestellt werden, oder AND und NOT aus NOR-Gattern. Man kann somit jede logische Schaltung allein durch NAND- oder NOR-Bausteine realisieren.

Größte Beliebtheit für die Entwicklung der Automatisierungs- und Computertechnik erlangten deshalb in den 1970er Jahren die Vierfach-NAND-Gatter 7400 (TTL) und 4011 (CMOS), sowie die Vierfach-NOR-Gatter 7402 (TTL) und 4001 (CMOS).

Die Anzahl von Gatteräquivalenten dient als Maß für die logische Komplexität einer Schaltung.

Das erste integrierte Logikgatter geht auf Jack Kilby im Jahr 1958 zurück und umfasste etwa zehn Bauteile. Zehn Jahre später fertigte Texas Instruments TTL-Schaltkreise (Serie 7400) in Großserie. Schnell wurden sie zur Basis der Industrieautomation.

Logikgatter werden mit Schaltsymbolen bezeichnet. Man unterscheidet folgende Typen von Logikgattern: XOR-Gatter, NOR-Gatter, NAND-Gatter, XNOR-Gatter, Und-Gatter, Oder-Gatter und Nicht-Gatter. Durch Verknüpfung mehrerer Logikgatter werden alle weiteren beliebig komplexeren logischen Funktionen erzeugt. Mehrere Logikgatter kann man zu einem Flipflop, Latch oder Multiplexer zusammenschalten, aus mehreren Flipflops kann man Datenspeicher und Zähler erstellen, und aus mehreren dieser Schaltungen kann man einen Mikroprozessor zusammenstellen.

Siehe auch

• Gatterlaufzeit
• Mathematische Logik
• Formelsammlung Logik
• Logikfamilie
• Standardzelldesign

Weblinks

Commons: Logikgatter – Sammlung von Bildern, Videos und Audiodateien