Operade
Eine Operade ist eine algebraische Struktur, die insbesondere in der Topologie von Bedeutung ist, aber auch in vielen anderen Anwendungen und dort Raum für Deformationen (Homotopie in der Topologie) der zugrundeliegenden Objekte lässt. Operaden bestehen allgemein aus einer Menge von Operationen (oder Funktionen) mit mehreren Eingängen (Inputs) und einem Ausgang und betrachtet wird die Algebra der Hintereinanderausführung dieser Operationen. Die Schachtelung der Hintereinanderausführung von Operationen wird dabei häufig geometrisch in Form von Bäumen dargestellt.
Sie wurden zuerst in der algebraischen Topologie Anfang der 1970er Jahre durch J. Michael Boardman und Rainer Vogt[1] sowie von J. Peter May[2] eingeführt, um die Homotopie höherer Schleifenräume zu verstehen. May prägte auch den Begriff aus Operation und Monade. Einen Aufschwung erlebte die Theorie der Operaden in den 1990er Jahren, als Maxim Kontsevich, Mikhail Kapranov und Victor Ginzburg zeigten, dass einige Dualitäten in der rationalen Homotopietheorie als Koszul-Dualitäten von Operaden erklärt werden konnten.[3] Sie dienen in der Homotopietheorie der Beschreibung der Hierarchien höherer Homotopien und fanden auch Anwendung zum Beispiel in der mathematischen Physik und Graphentheorie.
Definition[Bearbeiten | Quelltext bearbeiten]
Eine nicht-symmetrische Operade besteht aus der Folge der Mengen von Operationen auf n Variablen einschließlich der Identitätsoperation. Es wird folgende Verknüpfung einer Funktion auf n Variablen mit einer Operation auf m Variablen betrachtet:
wobei an der i-ten Stelle durch ersetzt wurde. Das ist eine Abbildung von . Graphisch lässt sich das als Komposition von Bäumen darstellen.
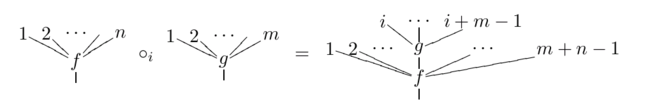
Die Identität operiert wie üblich auf : für alle .
Für die Komposition gilt folgendes Assoziativgesetz:
wenn man nur die Komposition bezüglich der ersten Variable betrachtet. Allgemein gelten komplexere Gesetze: Seien , und , dann ist:
- für
- für
- für
Diese Kompositionsregeln konstituieren auch die Definition nicht-symmetrischer Operaden. In vielen Anwendungsfällen liegt Symmetrie bezüglich der Permutation der Input-Variablen vor. Man definiert dann symmetrische Operaden, bei denen nach Wirkung der Permutationsgruppe die beiden Definitionsregeln für die Kompositionen erhalten bleiben (Wirkung der Identitätsoperation und die obigen Assoziativitätsregeln) und zusätzlich Equivarianzregeln:
Sei die symmetrische Gruppe von n Elementen, die auf P(n) wirke. Also für , ,,
für und der Blockpermutation, in der das i-te Element von durch ersetzt wird. Häufig werden symmetrische Operaden einfach als Operaden bezeichnet.
Man kann sich dafür zum Beispiel für die Elemente von P (n) Funktionen auf einem reellen Vektorraum vorstellen, die Elemente P(n) können aber auch als Abbildungen auf topologischen Räumen, Kettenkomplexen, Polytopen (wie Associahedren) oder ganz andere Objekte definiert sein, für die eine Komposition von Operatoren wie oben Sinn macht. Man sagt auch, eine symmetrische Operade wäre in jeder symmetrischen monoidalen Kategorie definierbar.
Beispiele[Bearbeiten | Quelltext bearbeiten]
Ein einfaches Beispiel für eine nicht-symmetrische Operade besteht aus der Addition (A) und Multiplikation (M) zweier Zahlen. Die Operationen sind Elemente von P(2). Die Komposition von A und M ist ein Element von P(3), explizit:
Nicht enthalten sind und , sie sind aber enthalten, falls man Permutationen der Inputs zulässt (symmetrische Operade).
Ein wichtiges Beispiel ist die Operade kleiner Scheiben (little disk operade). Man betrachtet dabei n verschiedene nicht überlappende Kreise in einem großen Kreis, die alle nummeriert sind. Sie bilden das Element Die Komposition von und besteht darin, dass P(k) in P(n) an Stelle der i-ten Scheibe eingefügt wird und dann eine Umnummerierung erfolgt. Besteht zum Beispiel P(2) aus den Scheiben 1,2 und wird in P(3) (bestehend aus den Scheiben (1,2,3) =(a,b,c)) an zweiter Stelle eingefügt (), so besteht die neue Figur aus den Scheiben (a, 1,2, c) die in neuer Nummerierung (1,2,3,4) heißen. Da die kleinen Scheiben permutiert werden können, ist es auch eine symmetrische Operade. Statt kleine Scheiben werden manchmal auch Kuben betrachtet.
Endomorphismen-Operade und Algebra von Operaden[Bearbeiten | Quelltext bearbeiten]
Ein wichtiges Beispiel ist die Operade der Endomorphismen , der Menge aller multilinearen Abbildungen (V sei ein Vektorraum). Die Komposition ist gegeben durch mit , , die nach abbildet, indem der Output von g als i-ter Input von f genommen wird. Durch die Wirkung der symmetrischen Gruppe wird der Input permutiert. Die Endomorphismen-Operade wird häufig für die Darstellung abstrakter Operaden genommen. Man spricht dann von einer P-Algebra einer Operade P. Algebren von Operaden stehen in derselben Beziehung zu Operaden wie Darstellungen von Gruppen bei Gruppen.
Anwendungen in der Topologie[Bearbeiten | Quelltext bearbeiten]
Ursprünglich wurden Operaden eingeführt für eine homotopieinvariante Charakterisierung von Schleifenräumen (Loop spaces). Für Schleifen mit fester Basis ist die zugehörige Operade durch Polytope gegeben, die sogenannten Assoziahedrone. Zum Beispiel besteht bei vier Schleifen (a,b,c,d) das Assoziahedron aus einem Pentagon, wobei die Ecken den Schleifenkombinationen (ab)(cd), ((ab)c)d), (a (bc))d, a((bc)d) und a(b(cd)) entsprechen.
Ein Raum ist ein topologischer Raum mit einer Homotopie-kohärenten Menge von Abbildungen
so dass Y eine Algebra über der (nicht-symmetrischen) Operade ist. Das A steht dabei für assoziativ und dafür dass die Menge der Abbildungen, oben mit dem Parameter versehen, beliebig hoch ist. Dann gilt der Satz:
- Ein zusammenhängender Raum vom Homotopietyp eines CW-Komplexes hat den Homotopietyp eines Schleifenraums für einen Raum genau dann, falls Y ein Raum ist.
Anwendungen in der mathematischen Physik[Bearbeiten | Quelltext bearbeiten]
Operaden haben in den 1990er Jahren und danach Anwendungen in der mathematischen Physik gefunden, zum Beispiel in Topologischen Quantenfeldtheorien und der Stringtheorie. Dort spielen Riemannsche Flächen mit Punktierungen und Markierungen eine Rolle und die Anwendung der kleine Scheiben Operade führt zu modularen Operaden. In der Stringfeldtheorie offener Strings spielt das Analogon von Räumen für Kettenkomplexe eine Rolle, die -Algebra, bei geschlossenen Strings und der Deformationsquantisierung die -Algebra, wo L für Liegruppen steht.
Eine weitere Anwendung ist der Beweis von Maxim Kontsevich, dass jedes klassische mechanische System in ein quantenmechanisches deformiert werden kann (Deformationsquantisierung von Poisson-Mannigfaltigkeiten). Genauer wird die Multiplikation auf den zugehörigen Observablen deformiert.
Einerseits wird der kleine Scheiben-Operade statt auf topologischen Räumen auf Kettenkomplexen betrachtet. Die neue Operade sei C. Andererseits betrachtet man Hochschild-Ko-Ketten auf der Menge der Observablen O. Das ergibt die Operade H der Hochschild-Ko-Ketten auf O, das heißt der Funktionen mit n Observablen als Input und einer Observabler als Output. Sie sind linear im Input. Eine Vermutung von Pierre Deligne besagt, dass H eine Algebra über der Operade C ist. Das wurde von Kontsevich[4] und anderen inzwischen bewiesen, wobei auch der Satz von Kontsevich über die Existenz der quantenmechanischen Deformation klassischer Systeme folgte.
Literatur[Bearbeiten | Quelltext bearbeiten]
- Martin Markl, Steve Shnider, James Stasheff: Operads in Algebra, Topology and Physics, Providence, American Mathematical Society, 2002
- J. P. May: The Geometry of Iterated Loop Spaces, Berlin, Springer-Verlag, 1972
- Jean-Louis Loday, Bruno Vallette: Algebraic Operads, Springer, Grundlehren der mathematischen Wissenschaften 346, Springer 2012
- James Stasheff: What Is…an Operad?, Notices of the American Mathematical Society, Band 51, Juni/Juli 2004, S. 630–631, pdf
- Jean-Louis Loday: Le renaissance de l' operads, Séminaire Bourbaki 792, 1994/95, numdam
- Bruno Vallette: Algebra + Homotopy = Operad, Arxiv 2012
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Krähmer, From computer algorithms to quantum field theory: an introduction to operads, Oberwolfach, Snapshots in modern mathematics
- Operad in ncatlab
- What is an Operad ?, Teil 1, Teil 2, math3ma
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Boardman, Vogt, Homotopy Invariant Algebraic Structures on Topological Spaces, Lecture Notes in Mathematics 347, Springer 1973
- ↑ May, The Geometry of Iterated Loop Spaces, Lecture Notes in Mathematics 271, Springer 1972
- ↑ Victor Ginzburg, Mikhail Kapranov: Koszul duality for operads, Duke Mathematical Journal, Band 76, 1994, S. 203–272.
- ↑ M. Kontsevich, Y. Soibelman, Deformations of algebras over operads and the Deligne conjecture, Conference Moshe Flato 1999, Band 1, Kluwer 2000, S. 255–307






















































