Stringtheorie
Als Stringtheorie bezeichnet man eine Sammlung eng verwandter hypothetischer physikalischer Modelle, die anstelle der Beschreibung von Elementarteilchen in den gewohnten Modellen der Quantenfeldtheorie als punktförmige Teilchen (räumliche Dimension Null) in der Raum-Zeit sogenannte Strings (englisch für Fäden oder Saiten) als fundamentale Objekte mit eindimensionaler räumlicher Ausdehnung verwenden. In Erweiterungen der Stringtheorie werden auch höherdimensionale Objekte betrachtet. Stringtheorien wurden in den 1960er Jahren zur Beschreibung der starken Wechselwirkung (Quantenchromodynamik) eingeführt.
Seit den 1980er Jahren erlebte die Stringtheorie einen starken Aufschwung. Sie gilt seitdem als Kandidat für eine alle Naturkräfte vereinheitlichende Theorie, die das Standardmodell der Elementarteilchenphysik und die Gravitation miteinander verbindet. Diskutiert wird dabei vor allem die supersymmetrische Version der Stringtheorie („Superstringtheorie“). Die Supersymmetrie sagt neue, supersymmetrische Partnerteilchen für alle Bosonen und Fermionen voraus. Zum Aufschwung der Superstringtheorie trug erheblich bei, dass sie konkrete Vorhersagen für die Symmetriegruppen einer Großen Vereinheitlichten Theorie (GUT) machte. Des Weiteren fanden Vorhersagen zur Betrachtung von Quantenfeldtheorien (wie das holografische Prinzip in AdS/CFT) große Beachtung.[1] In den 1990er Jahren stellte sich heraus, dass die bis dahin bekannten Superstringtheorien und die 11-dimensionale Supergravitation miteinander verbunden als Teil einer umfassenderen Theorie („M-Theorie“ genannt) betrachtet werden können. Letztere umfasst auch höherdimensionale Objekte (sogenannte „Brane“). Die Stringtheorie führte zu einem engen Austausch zwischen verschiedenen Gebieten der Mathematik und theoretischen Physik.[1][2]
Die Stringtheorie ist gegenwärtig weder experimentell bestätigt noch widerlegt. Dies liegt unter anderem daran, dass die Vereinigung der Naturkräfte auf Energieskalen (siehe Planck-Skala), die in absehbarer Zeit nicht erreichbar sind, erwartet wird. Die Stringtheorie wird daher seit den 2000er Jahren sowohl innerhalb als auch außerhalb der Physik kritisiert. Die Kritik richtet sich dabei auch auf die einseitige und außergewöhnliche Bindung von Forschungsressourcen in Gebieten, die Anwendungen fern stehen, und erfolgte besonders dezidiert von Theoretikern, die alternative Theorien der Quantengravitation verfolgen (wie die Schleifenquantengravitation).[3][4] Zudem tauchten bei der konkreten mathematischen Durcharbeitung der Stringtheorie unerwartet viele Varianten auf, die die Erfolgsaussichten, alle Naturkräfte über die Stringtheorie zu vereinheitlichen, in weite Ferne rücken.
Heute gilt die Stringtheorie zwar als „verlockend“ und „mathematisch sehr elegant“, da sie aber keine Vorhersagen macht, die aktuell experimentell bestätigt werden könnten, wird ihre praktische Bedeutung für die Teilchenphysik in Abrede gestellt.[5]
Überblick[Bearbeiten | Quelltext bearbeiten]

Im Gegensatz zum Standardmodell der Teilchenphysik sind bei der Stringtheorie die fundamentalen Bausteine, aus denen sich die Welt zusammensetzt, keine Teilchen im Sinne von Punkten (also nulldimensionalen Objekten), sondern vibrierende eindimensionale Objekte. Diese eindimensionalen Objekte werden Strings genannt. Elementarteilchen kann man sich als Schwingungsanregung der Strings vorstellen, wobei die Frequenz nach der Quantenmechanik einer Energie entspricht.
In Weiterentwicklungen der Stringtheorie, den sogenannten Brane-Theorien, werden als Basisobjekte nicht nur eindimensionale (bzw. bei Einschluss der Zeit (1+1)-dimensionale) Strings angesehen, sondern auch höherdimensionale Objekte („Brane“ genannt)[6] verwendet.
Durch Annahme dieser eindimensionalen Struktur der Strings treten automatisch viele erwünschte Eigenschaften einer eher fundamentalen Theorie der Physik hervor. Am meisten sticht hervor, dass jede Stringtheorie, die mit der Quantenmechanik vereinbar ist, eine Quantengravitation beinhalten muss.
In der Stringtheorie werden Probleme vermieden, die durch divergierende Schleifenintegrale und die zu ihrer Kompensation entwickelten Renormierungstheorien entstehen. Divergenzen (unendliche Werte der Integrale) ergeben sich speziell für Punktteilchen aus ihrer Selbstwechselwirkung, die bei ausgedehnten, z. B. eindimensionalen, Objekten „verschmiert“ und damit abgemildert wird. Vereinfacht kann man sich das so vorstellen: Betrachtet man die für die Quantenmechanik grundlegende Heisenbergsche Unschärferelation , stellt man Folgendes fest: Wenn , dann . Das bedeutet, dass bei einer verschwindenden Distanz ein unendlicher Impuls entstehen würde. In der Stringtheorie wird nun der Fall vermieden und es existiert eine obere Grenze, der Impuls kann nur einen großen, aber endlichen Wert haben, auf diesem Weg werden die Divergenzen in der Theorie vermieden. Die Unschärferelation wird für Strings modifiziert zu
- mit ,
wobei die Stringspannung beschreibt. Der neue Term wird hier benutzt, um eine minimale Distanz festzulegen. Diese minimale Distanz ist nun gegeben durch:
Wenn nun gilt, tritt das Problem von Punktinteraktionen nicht auf, weil diese ausgeschlossen sind.
Die charakteristische Längenskala der Strings müsste in der Größenordnung der Plancklänge liegen, der Größe, unter der Effekte der Quantengravitation wichtig werden:
Auf viel größeren Längenskalen, wie sie heute in Laboratorien zugänglich sind, wären diese Objekte nicht von nulldimensionalen punktförmigen Partikeln zu unterscheiden. Trotzdem würden die Vibrationszustände und die Struktur dieser winzigen Strings sie als verschiedene Elementarteilchen des Standardmodells der Elementarteilchenphysik erscheinen lassen. Zum Beispiel würde ein Schwingungszustand des Strings mit einem Photon assoziiert werden, ein anderer Zustand mit einem Quark. Diese vereinigende Wirkung der Stringtheorie ist eine ihrer größten Stärken, doch reproduziert noch keine bekannte Lösung dieser Theorie genau die Vielzahl von Teilchen, die das Standardmodell kennt.
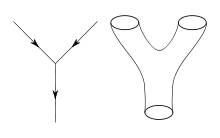
In der Raumzeit überstreicht ein Partikel eine Linie, Weltlinie genannt: Das Teilchen hat keine räumliche Ausdehnung, aber es bewegt sich entlang der „Zeit“. Ein String besitzt dagegen eine zweidimensionale Weltfläche („World Sheet“), da er auch eine räumlich eindimensionale Ausdehnung hat. Die Wechselwirkungen der Elementarteilchen, in der üblichen Quantenfeldtheorie der Punktteilchen mit Feynman-Diagrammen in der Raum-Zeit beschrieben, kann man sich durch „Verdickung“ dieser Feynman-Diagramme in einer Raumrichtung vorstellen (siehe obiges Bild).
Arten von Strings[Bearbeiten | Quelltext bearbeiten]
Geschlossene und offene Strings[Bearbeiten | Quelltext bearbeiten]
Strings können entweder offen oder geschlossen sein. Ein „geschlossener String“ besitzt keine Endpunkte und ist daher in seiner Topologie einem Kreis äquivalent. Ein „offener String“ hat zwei Enden und ist topologisch äquivalent zu einer Strecke. Nicht alle Stringtheorien enthalten offene Strings, aber jede Theorie muss geschlossene Strings enthalten, da Wechselwirkungen offener Strings immer geschlossene erzeugen können.
Die älteste Stringtheorie, die offene Strings enthielt, war die Typ-1-Stringtheorie.
Mit offenen wie geschlossenen Strings sind immer charakteristische Schwingungsarten (Moden) verbunden. Eine bestimmte Vibration eines geschlossenen Strings kann als Graviton identifiziert werden. In gewissen Stringtheorien stellt die Schwingung mit der niedrigsten Energie eines offenen Strings ein Tachyon dar. Andere Schwingungsmoden offener Strings zeigen die Eigenschaften von Photonen oder Gluonen.
Orientierung[Bearbeiten | Quelltext bearbeiten]
Strings können auch eine „Orientierung“ besitzen, die man sich als stringinternen Pfeil denken kann, der sie von Strings mit der entgegengesetzten Orientierung unterscheidet. Im Gegensatz dazu gibt es auch den „nichtorientierten String“, dem kein solcher Pfeil zugewiesen werden kann.
Bosonische Stringtheorie [Bearbeiten | Quelltext bearbeiten]
Nambu-Goto-Wirkung[Bearbeiten | Quelltext bearbeiten]
Die Nambu-Goto-Wirkung ist die einfachste Form der Wirkung einer Stringtheorie, beschreibt eine bosonische Stringtheorie (ohne Fermionen) und wurde um 1970 von Yōichirō Nambu[7] und Tetsuo Gotō[8] eingeführt. Da die Lichtkegelquantisierung der Nambu-Goto-Wirkung nicht manifest kovariant ist, bietet sich hier die äquivalente, aber kompliziertere Polyakov-Wirkung an. Ein Punktteilchen, das sich durch die Raumzeit bewegt, beschreibt eine eindimensionale Kurve, auch Weltlinie genannt. Analog dazu beschreibt ein eindimensionaler String, der sich durch die Raumzeit bewegt, eine zweidimensionale Weltfläche. Die Weltfläche eines Strings wird beschrieben durch eine Parametrisierung mit , wobei als Zeitparameter interpretiert werden kann und den String parametrisiert, für geschlossene Strings gilt . Sei nun der Tangentialraum der Weltfläche aufgespannt durch die Vektoren und . Um die Weltfläche zu beschreiben, kann vom Analogon der bekannten euklidischen Flächenformel ausgegangen werden:

Da der Radikand im Fall der Strings negativ ist (höherdimensionaler Minkowskiraum, eine der Richtungen der Strings zeitartig, die andere raumartig), muss noch das Vorzeichen geändert werden, indem einfach die Terme vertauscht werden; setzt man nun die Tangentialvektoren ein, führt dies auf
mit dem metrischen Tensor und der Determinantenbildung bezüglich .
Nach der Multiplikation mit entsprechenden Einheiten, um das Funktional konsistent mit einer physikalischen Wirkung zu machen, erhält man nun die Nambu-Goto-Wirkung für geschlossene und offene relativistische Strings in einer -dimensionalen Raumzeit, wobei die Lichtgeschwindigkeit ist und die oben eingeführte Stringspannung:
- mit
- und
Die Impulsdichten ergeben sich zu:
Die Nambu-Goto-Wirkung kann auch in manifester reparametrisierungsinvarianter Form geschrieben werden, wobei , im Detail . Dies führt auf:
Die Form dieser Wirkung eignet sich auch zur Verallgemeinerung auf Objekte, die eine höhere Dimensionalität als Strings haben, wie z. B. D-Brane.
Im Vergleich dazu war die Wirkung für ein relativistisches Punktteilchen (wobei das Vorzeichen für den Term unter dem Wurzelzeichen so gewählt wird, dass der Term unter der Wurzel für zeitartige Weltlinien positiv ist).
Polyakov-Wirkung[Bearbeiten | Quelltext bearbeiten]
Die Quadratwurzel der Nambu-Goto Wirkung hat entscheidende Nachteile bei der Quantisierung, eine einfachere Form ist die Polyakov-Wirkung, auch String-Sigma-Modell genannt:
- ,
wobei eine zusätzliche Weltflächenmetrik ist (). Reparametrisierungsinvarianz und Skalierungsinvarianz erlauben es, das Hilfsfeld als zu wählen, worauf sich die Polyakov-Wirkung vereinfacht zu
für Bewegungsgleichungen in einer flachen Minkowski-Raumzeit.
Symmetrien der Polyakov-Wirkung[Bearbeiten | Quelltext bearbeiten]
- Poincaré-Transformation: Globale Symmetrie der Weltflächen-Felder mit mit .
- Reparametrisierungen: Die Polyakov-Wirkung ist klassisch äquivalent zur Nambu-Goto-Wirkung und daher auch lokal reparametrisierungsinvariant unter und .
- Weyl-Transformationen: Lokal invariant unter Reskalierung und .
Bewegungsgleichungen und Randbedingungen[Bearbeiten | Quelltext bearbeiten]
Nehmen wir die Bewegung in der flachen Minkowski-Raumzeit an. Die Bewegungsgleichungen der Wirkung beschreiben eindeutig Wellengleichungen , mit verschwindendem Energie-Impuls-Tensor als weitere Einschränkung.
Für einen geschlossenen String gelten nun die periodischen Randbedingungen
- .
Für einen offenen String gilt die Neumann-Randbedingung (String, dessen Endpunkte sich bewegen)
- für ,
für einen offenen String mit Dirichlet-Randbedingung (beide Endpunkte des Strings „auf gleicher Höhe“ fixiert)
- und .
Lösung der Bewegungsgleichungen[Bearbeiten | Quelltext bearbeiten]
Um Lösungen der Bewegungsgleichungen zu finden, bietet sich eine Formulierung in Lichtkegel-Koordinaten an mit
- mit Ableitungen und Wellengleichung .
Geschlossener String[Bearbeiten | Quelltext bearbeiten]
Die allgemeine Lösung der Wellengleichung mit Randbedingungen für geschlossene Strings ist gegeben durch
- ,
wobei der Parameter für zur Vereinfachung gesetzt wurde. bezeichnet man bei einem geschlossenen String als Rechts-Beweger und als Links-Beweger.
Offener String[Bearbeiten | Quelltext bearbeiten]
Die allgemeine Lösung für offene Strings mit Neumann-Randbedingungen ist gegeben durch
- .
ist die Position des Massenschwerpunktes und der Gesamtimpuls des Strings; der exponentielle Term beschreibt die angeregten Zustände.
Entwicklung zu Superstringtheorie und M-Theorie [Bearbeiten | Quelltext bearbeiten]


Ursprünglich war die Entdeckung der Strings (als „duale Modelle“) eine Formel von Gabriele Veneziano aus dem Jahre 1968 im Rahmen der Streumatrix-Theorie stark wechselwirkender Teilchen. 1970 gaben Yōichirō Nambu, Holger Bech Nielsen und Leonard Susskind eine Interpretation in Form von eindimensionalen Strings. Zunächst nur für Teilchen mit ganzzahligem Spin (Bosonen) formuliert, folgte schon bald 1971 die Beschreibung von Teilchen mit halbzahligem Spin (Fermionen) im Stringmodell durch André Neveu, John Schwarz und Pierre Ramond. Daraus ergab sich im Laufe der 1970er Jahre die Einsicht, dass in den Stringmodellen Supersymmetrie zwischen Bosonen und Fermionen bestehen muss. Anfangs bestand die Hoffnung, mit Strings die starke Wechselwirkung zu beschreiben, doch die Entdeckung, dass die Quantentheorie der Strings nur in 26 Dimensionen (Bosonen-String) bzw. 10 Dimensionen (Superstring) möglich ist, versetzte der Theorie um 1974 zunächst einen Dämpfer. Durch die Arbeit von Joel Scherk u. a. wurde jedoch bald darauf klar, dass eine Superstring-Theorie als Kandidat für eine vereinheitlichte Theorie der Naturkräfte inklusive der Gravitation in Frage käme. Die Gravitation ergibt sich bei geschlossenen Strings automatisch als masselose Spin-2-Anregung, die übrigen bekannten Naturkräfte (alles Eichtheorien) entsprechen masselosen Spin-1-Bosonenanregungen. Die zusätzlichen Dimensionen müssten dann auf irgendeine Weise „zusammengerollt“ (kompaktifiziert) werden, wie schon bei den seit den 1930er Jahren bekannten Kaluza-Klein-Theorien (siehe Kaluza-Klein-Kompaktifizierung).
1984 entdeckten Michael Green und John Schwarz, dass sich in Superstringtheorien die Ein-Schleifen-Divergenzen in der Störungstheorie nur bei ganz bestimmten Symmetriegruppen (der Drehgruppe in 32 Dimensionen SO(32) und der speziellen Lie-Gruppe E8) aufheben. Außerdem wurde bei diesen Symmetrien das Auftreten von „Anomalien“ vermieden, das heißt ein Symmetriebruch aufgrund quantenmechanischer Effekte in bestimmten Wechselwirkungsdiagrammen. Dies führte zu einer Neubelebung der Theorie und einer ganzen Reihe weiterer Entdeckungen (sogenannte „Erste Superstring-Revolution“). Sie zeigten nämlich, dass die Theorie für die Eichtheorien, die im Niedrigenergie-Grenzfall der Stringtheorie das Teilchenspektrum beschreiben, erhebliche Einschränkungen ergibt. Außerdem konstruierten Green und Schwarz explizit die ersten Superstringtheorien, deren Existenz vorher nur vermutet worden war.
Um nach der „Kompaktifizierung“ (dem „Einrollen“) der Extra-Dimensionen ein realistisches Modell der Elementarteilchen in den beobachtbaren 4 Dimensionen zu bekommen, folgerten Edward Witten u. a. außerdem eine Reihe von Einschränkungen für die Kompaktifizierungs-Mannigfaltigkeit (bevorzugt wurden sogenannte Calabi-Yau-Mannigfaltigkeiten).
Zunächst bestand die Hoffnung, auch hier stark einschränkende Prinzipien zu finden, doch entdeckte man im Laufe der 1980er Jahre, dass dies nicht der Fall war und die Theorie Raum für eine sehr hohe Zahl möglicher „Vakua“ gab.
Als Kandidaten für die Superstring-Theorien ergaben sich in den 1980er Jahren folgende fünf Theorien:
- Die Typ-I-Stringtheorie, mit offenen Enden der Strings (aber Ankopplung an geschlossene Strings durch Kontakt der Enden, entsprechend gravitativer Wechselwirkung) und der Symmetrie SO(32) mit Ladung an den Enden.
- Die Typ-IIA- und die Typ-IIB-Stringtheorie, mit geschlossenen Strings; in Typ II A haben die masselosen Fermionen beide Händigkeiten (links/rechts), in II B nur eine Händigkeit (Chiralität).
- Zwei Varianten der heterotischen Stringtheorie, geschlossene Strings, die unter Bezug auf ihre Symmetriegruppen E8 × E8 bzw. SO(32) gelegentlich als E-heterotische und O-heterotische Stringtheorie bezeichnet werden. Sie wurden vom „Princeton-String-Quartett“ um David Gross gefunden. In ihnen werden rechts- und linkshändige Moden (RH, LH) durch unterschiedliche Theorien beschrieben: RH durch eine 10-dimensionale Superstringtheorie (Beschreibung von Bosonen und Fermionen), LH durch eine 26-dimensionale bosonische Stringtheorie, die aber zu 10 Dimensionen kompaktifiziert, wobei die Eichfeld-Ladungen entstehen, E8 × E8 bzw. SO(32).
Edward Witten vermutete 1995, dass die verschiedenen Stringtheorie-Typen verschiedene Approximationen einer umfassenderen Theorie, der M-Theorie, sind. Es ist noch keine vollständige und einheitliche Formulierung dieser Theorie gelungen, sie ist aber Gegenstand intensiver Forschung. Argumente dafür, dass es sich bei diesen Theorien um Aspekte einer einzelnen Theorie handelt, wurden durch Aufzeigen von Dualitäten zwischen den einzelnen Stringtheorien erbracht, das heißt, es wurde gezeigt, dass sie das gleiche System, nur z. B. im Bereich verschieden starker Kopplungskonstanten, beschreiben. Ähnliche Dualitäten wurden auch für verschiedene Lösungen („Vakua“, das heißt Grundzustände) der Stringtheorie gefunden. Dies war die sogenannte „Zweite Superstring-Revolution“, die zu einer Neubelebung der damals wieder etwas stagnierenden Theorie Mitte der 1990er Jahre führte.
Ein interessantes Ergebnis dieser Vereinigung der Teiltheorien war, dass die elfdimensionale Supergravitation, die davor etwas in die Isolation geraten war, als weiterer Grenzfall der M-Theorie erkannt wurde. Diese enthält aber keine Strings, sondern ist eine Teilchen-Approximation von zwei- und fünfdimensionalen Branen. Das verdeutlicht, dass eine allgemeine Stringtheorie mehr beschreibt als nur eindimensionale Strings, und in der Tat hat sich Ende der 1990er Jahre gezeigt, dass höherdimensionale Branen (D-Branes) eine wichtige Rolle in der Stringtheorie spielen (Joseph Polchinski).
Die Stringtheorie hat sich über die Jahre zu einem sehr aktiven Forschungsgebiet mit einer großen Anzahl von Veröffentlichungen pro Jahr entwickelt, was seinen Niederschlag unter anderem darin findet, dass einige beteiligte Forscher (insbesondere Edward Witten) zu den meistzitierten[9] Wissenschaftlern der gesamten Physik gehören.
Experimentelle Überprüfung[Bearbeiten | Quelltext bearbeiten]
Gemäß der Stringtheorie gibt es ein Vibrationsspektrum von unendlich vielen Schwingungsmodi, die aber viel zu hohe Massen (Energien) haben, um direkt beobachtet werden zu können.[10] Berücksichtigt man die geringe Ausdehnung der Strings in der Größenordnung der Planck-Länge, so bedeutet das nach einem quantenmechanischen Standardargument, dass die Vibrationsmodi Massen besitzen, die ein Vielfaches von ca. 1019 GeV betragen. Das liegt um viele Größenordnungen über dem, was man heute beobachten kann; ein direkter Nachweis dieser Vibrationsmodi ist deshalb nicht möglich. Daher versucht man für die Stringtheorie spezifische Eigenschaften für die niedrigenergetischen, im Vergleich zur Planckmasse fast „masselosen“ Anregungen zu finden. Dazu müsste man aber den Kompaktifizierungsmechanismus von 10 oder 11 zu 4 Dimensionen – oder von der Planckmasse von 1019 bis zur W-Bosonenmasse von ca. 80 GeV oder der Protonmasse von ca. 1 GeV – in der Stringtheorie besser verstehen, was bisher nicht der Fall ist.
Trotzdem gibt es bereits eine Fülle diskutierter Lösungen für den beobachtbaren Niedrigenergiesektor in 4 Raum-Zeit-Dimensionen (sogenannte String-Phänomenologie).[11]
Es war erwartet worden, dass die Experimente z. B. mit dem Large Hadron Collider (LHC) in der 2. Hälfte der 2010er Jahre Belege für die Existenz supersymmetrischer Teilchen und damit für die Richtigkeit der Stringtheorie erbringen könnten.[12] Bis 2019 sind keine supersymmetrischen Teilchen gefunden worden, und es gibt auch für den Mechanismus der Supersymmetriebrechung bei den Stringtheoretikern bisher keine Übereinstimmung.
Als eine weitere Vorhersage der Stringtheorie gelten Extradimensionen. Als eine Möglichkeit zur Überprüfung der Stringtheorie wurden zum Beispiel[13] ein Axion-Monodromie-Mechanismus und andere mögliche Hinweise auf die Kompaktifizierung der Extradimensionen in der kosmischen Hintergrundstrahlung (CMB) diskutiert. Die Auswirkung von primordialen Gravitationswellen könnte sich in Mustern in der Polarisation der CMB niederschlagen, wonach Bicep und andere Experimente suchen, und man bemüht sich Modelle des Inflationspotentials aus der Stringtheorie abzuleiten, die dann so getestet werden können.
Es kann sich auch in der Untersuchung von Modellen zeigen, dass sie theoretisch inkonsistent sind bzw. mit allgemein akzeptierten Annahmen der Physik nicht übereinstimmen. Daher wurde zum Beispiel die bosonische Stringtheorie ausgeschlossen. Als Test der Quantengravitation gilt allgemein, wie gut eine Theorie mikroskopisch die Entropie Schwarzer Löcher erklären kann. Es wurden seit 2005 verschiedene Sumpfland-Hypothesen vorgeschlagen, um die große Anzahl möglicher String-Vakua (String Landscape) einzugrenzen (initiiert von Cumrun Vafa). Sumpfland meint dabei physikalisch auszuschließende Bereiche der String Landschaften. 2018 stellte Vafa seine kontrovers diskutierte De-Sitter-Sumpfland-Hypothese auf, die, falls sie zutrifft, zu einem Widerspruch mit kosmologischen Implikationen der Stringtheorie führen würde (und auch für Inflationsmodelle ein Problem ist). Sie sagt eine Quintessenz-Form der Dunklen Energie voraus, was astronomisch überprüft werden kann (und im Dark Energy Survey geplant ist).
Die Stringtheorie findet auch in der Festkörperphysik Anwendung, insbesondere über die duale Beschreibung konformer Yang-Mills-Theorien auf Oberflächen und Stringtheorien in den Volumina, die von der Oberfläche umschlossen werden, in der AdS/CFT-Korrespondenz.[14] Sogar in der Hydrodynamik findet die Stringtheorie so Anwendung (Navier-Stokes-Gleichung im Skalierungsgrenzfall einerseits, Einstein-Gravitation als Grenzfall der Stringtheorie andererseits in der dualen Beschreibung).
Kritik[Bearbeiten | Quelltext bearbeiten]
An der Stringtheorie entzündete sich seit den 2000er Jahren eine zum Teil heftige Kritik. Der Nobelpreisträger und Festkörperphysiker Robert Laughlin, der vor allem die starke Bindung von Forschungsressourcen auf einem den Anwendungen fernstehenden Gebiet kritisiert, fasst es wie folgt zusammen: „Weit entfernt von einer wunderbaren technologischen Hoffnung auf eine bessere Zukunft ist die Stringtheorie die tragische Konsequenz eines überholten Glaubenssystems.“ (“Far from a wonderful technological hope for a greater tomorrow, string theory is the tragic consequence of an obsolete belief system.”)[15] Der Nobelpreisträger Gerard ’t Hooft (2013) kritisiert wie Vertreter konkurrierender Theorien zur Quantengravitation (wie der Schleifenquantengravitation, Carlo Rovelli, Lee Smolin), dass die Stringtheorie zu sehr konventionellen Auffassungen der Rolle der Raumzeit in der Quantenmechanik verhaftet ist.[4] Carlo Rovelli kritisiert an der Stringtheorie, dass sie sich als nicht funktionsfähig erweise und dennoch auch nach Jahrzehnten mit einem Aufwand, der seinesgleichen sucht, noch daran weitergearbeitet werde (“it does not work, therefore let’s develop it further”).[3] Einige Kritiker gehen sogar so weit, dass sie der Stringtheorie die Rolle einer falsifizierbaren wissenschaftlichen Theorie absprechen. Peter Woit verwendete dafür ein bekanntes Zitat des für seine Scharfzüngigkeit bekannten Nobelpreisträgers Wolfgang Pauli, der grundsätzlich experimentell nicht überprüfbare (und auch nicht falsifizierbare) Theorien für physikalische Phänomene so charakterisierte, dass sie nicht einmal falsch seien (englisch not even wrong, der Titel von Woits Buch).
Siehe auch[Bearbeiten | Quelltext bearbeiten]
Literatur[Bearbeiten | Quelltext bearbeiten]
Populärwissenschaftliche Bücher[Bearbeiten | Quelltext bearbeiten]
- Brian Greene: The Elegant Universe: Superstrings, Hidden Dimensions, and the Quest for the Ultimate Theory. Vintage Books, 2000, ISBN 0-393-05858-1. (Das elegante Universum. 2002, Goldmann Verlag, 2005, ISBN 3-442-76026-7.)
- Brian Greene: Der Stoff, aus dem der Kosmos ist – Raum, Zeit und die Beschaffenheit der Wirklichkeit. Siedler Verlag, 2004, ISBN 3-88680-738-X. (Goldmann TB 2008; Originalausgabe The fabric of the cosmos.)
- Steven Gubser: The little book of string theory. Princeton University Press, 2010.
- Michio Kaku: Im Hyperraum – Eine Reise durch Zeittunnel und Paralleluniversen. Rowohlt, 1998, ISBN 3-499-60360-8.
- Michio Kaku: Die Physik der unsichtbaren Dimensionen – Eine Reise durch Zeittunnel und Paralleluniversen. Rowohlt, 2013, ISBN 978-3-499-61509-2.
- Lisa Randall: Verborgene Universen – Eine Reise in den extradimensionalen Raum. Fischer TB, 2010, ISBN 978-3-10-062805-3.
- Dieter Lüst: Quantenfische: Die Stringtheorie und die Suche nach der Weltformel. C.H. Beck, München 2011, ISBN 978-3-406-62285-4.
- Paul Davies, Julian R. Brown: Superstrings. Eine Allumfassende Theorie der Natur in der Diskussion. DTV, 1996, ISBN 3-423-30035-3 (zuerst 1988).
- Frederick David Peat: Superstrings, kosmische Fäden. Hoffmann und Campe, Hamburg 1989, ISBN 3-455-08340-4.
Von Kritikern der Stringtheorie:
- Peter Woit: Not Even Wrong. The Failure of String Theory and the Continuing Challenge to Unify the Laws of Physics. Jonathan Cape, 2006, ISBN 0-224-07605-1.
- Lee Smolin: Die Zukunft der Physik: Probleme der String-Theorie und wie es weitergeht. Deutsche Verlags-Anstalt, München 2009. Siehe auch The Trouble with Physics.
- Robert B. Laughlin: Abschied von der Weltformel. Die Neuerfindung der Physik. Piper Verlag, München 2007, ISBN 978-3-492-04718-0 (A different universe – Reinventing Physics from the bottom down. Basic Books, New York, 2005.)
- Sabine Hossenfelder: Das hässliche Universum: Warum unsere Suche nach Schönheit die Physik in die Sackgasse führt. S. Fischer 2018, ISBN 978-3-10-397246-7 (Lost in Math: How Beauty Leads Physics Astray. Basic Books, 2018).
Lehrbücher[Bearbeiten | Quelltext bearbeiten]
- Katrin Becker, Melanie Becker, John Schwarz: String Theory and M-Theory: A Modern Introduction. Cambridge University Press, 2007, ISBN 978-0-521-86069-7.
- Ralph Blumenhagen, Dieter Lüst, Stefan Theisen: Basic concepts of string theory. Springer, 2013.
- Michael Green, John Schwarz, Edward Witten: Superstring theory. Cambridge University Press, 1987.
- Vol. 1: Introduction. ISBN 0-521-35752-7.
- Vol. 2: Loop amplitudes, anomalies and phenomenology. ISBN 0-521-35753-5.
- Luis E. Ibáñez, Angel M. Uranga: String theory and particle physics. An introduction to String Phenomenology. Cambridge University Press, 2012, ISBN 978-0-521-51752-2.
- Clifford Johnson: D-branes. Cambridge University Press, 2003, ISBN 0-521-80912-6.
- Elias Kiritsis: String Theory in a Nutshell. Princeton University Press, 2007, ISBN 978-0-691-12230-4.
- Michio Kaku: Introduction to Superstrings and M-Theory. 2. Auflage. Springer, 1999, ISBN 0-387-98589-1.
- Dieter Lüst, Stefan Theisen: Lectures on String Theory. (= Lecture Notes in Physics. No. 346). Springer Verlag, 1989, ISBN 0-387-51882-7.
- Joseph Polchinski: String Theory. Cambridge University Press, 1998.
- Vol. 1: An introduction to the bosonic string. ISBN 0-521-63303-6.
- Vol. 2: Superstring theory and beyond. ISBN 0-521-63304-4.
- Barton Zwiebach: A First Course in String Theory. Cambridge University Press, 2004, ISBN 0-521-83143-1.
Aufsätze[Bearbeiten | Quelltext bearbeiten]
- Michael Green: Superstrings. In: Scientific American. November 1986, (damtp.cam.ac.uk).
- Edward Witten: What every physicist should know about string theory. In: Physics Today. November 2015, sns.ias.edu (PDF).
Weblinks[Bearbeiten | Quelltext bearbeiten]
- String Theory Wiki Bücher und Skripts zu allen Teilbereichen der Stringtheorie (englisch)
- Kurze Einführung in Stringtheorie (deutsch)
- Auf der Suche nach den verborgenen Universen, Spiegel Online, 29. Februar 2008
- Superstrings! – Online-Einführung in Superstringtheorie von John M. Pierre (englisch)
- The Official String Theory Web Site – Überblick über Stringtheorie (englisch)
- The Elegant Universe – TV-Dokumentation von Brian Greene (Video auf der Webseite verfügbar, englisch)
- The Elegant Universe – Interview mit Sheldon Glashow zur Stringtheorie (englisch)
- Frank Grotelüschen: Strings in der Krise – Physiker streiten um den rechten Weg zur Weltformel – Deutschlandfunk – Wissenschaft im Brennpunkt vom 17. Dezember 2006
- Literaturlisten zum Thema, Massachusetts Institute of Technology
- Polchinski: What is string theory? Vorlesungen, 1994 (englisch), arxiv:hep-th/9411028
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ a b K. C. Cole, The Strange second life of string theory, Quanta Magazine, 15. September 2016
- ↑ Robbert Dijkgraaf, Quantum questions inspire new math, Quanta Magazine, 30. März 2017
- ↑ a b C. Rovelli: A Critical Look at Strings. In: Foundations of Physics. Band 43, Nr. 1, 2013, S. 8–20, doi:10.1007/s10701-011-9599-3.
- ↑ a b ’t Hooft: On the Foundations of Superstring Theory. In: Foundations of Physics. Band 43, Nr. 1, 2013, S. 46–53, doi:10.1007/s10701-012-9682-4.
- ↑ Alexander Belyaev, Douglas Ross: The Basics of Nuclear and Particle Physics (= Undergraduate Texts in Physics). Springer International Publishing, Cham 2021, ISBN 978-3-03080115-1, S. 357, doi:10.1007/978-3-030-80116-8 (springer.com [abgerufen am 5. Juni 2023]).
- ↑ Nach der englischen Endung von Membran, mit Anklang an das englische Wort „brain“ für Gehirn. Zuerst wurden zweidimensionale Objekte diskutiert, die Membranes, später auch höherdimensionale p-Branes, insbesondere die D-Branes, bei denen das D für Dirichlet-Randbedingung steht.
- ↑ Vorlesungen von Nambu auf einem Symposium in Kopenhagen August 1970, veröffentlicht in Nambu, Selected Papers, 1995.
- ↑ Tetsuo Gotō: Relativistic quantum mechanics of one dimensional mechanical continuum and subsidiary condition of dual resonance model. In: Progress Theoretical Physics. Band 46, 1971, S. 1560.
- ↑ Z. B. mit dem H-Index gemessen.
- ↑ Siehe z. B. Jan Louis: Die vielen Saiten der Stringtheorie. In: Physik Journal. Band 7, 2008, Nr. 6, S. 29–35.
- ↑ Siehe zum Beispiel Luis E. Ibáñez, Angel M. Uranga: String theory and particle physics. An introduction to String Phenomenology. Cambridge University Press, 2012.
- ↑ A range of experiments at CERN investigate physics from cosmic rays to supersymmetry. CERN, abgerufen am 12. August 2016.
- ↑ Gary Shiu, Bret Underwood: Observing the Geometry of Warped Compactification via Cosmic Inflation. In: Physical Review Letters. Band 98, 2007, 051301, arxiv:hep-th/0610151.
- ↑ Horatiu Nastase: String theory methods in condensed matter physics. Cambridge UP 2017
- ↑ String theory: Is it science’s ultimate dead end? In: The Guardian. 8. Oktober 2006 (theguardian.com).





























































