Reguläre Grammatik
Eine reguläre Grammatik ist in der Informatik eine formale Grammatik vom Typ 3 der Chomsky-Hierarchie. Die von solchen Grammatiken erzeugten Sprachen heißen reguläre Sprachen.[1]
Definition[Bearbeiten | Quelltext bearbeiten]
Eine reguläre Grammatik (mit Vokabular , Terminalalphabet , Menge der Nichtterminalen (Variablen) , Produktionsregeln und Startsymbol )[2] ist eine kontextfreie Grammatik, deren Produktionsregeln bestimmten weiteren Einschränkungen genügen. Es gibt zwei verschiedene Arten von Einschränkungen, die dann spezifisch rechtsreguläre bzw. linksreguläre Grammatiken definieren. Da man sich aus praktischen Gründen bei Anwendungen meist an die rechtsregulären Grammatiken hält, sagt man oft auch kurz „regulär“, wo man eigentlich „rechtsregulär“ meint (ansonsten kann regulär linksregulär oder rechtsregulär bedeuten).[3]
Für Produktionsregeln regulärer Grammatiken darf die linke Seite immer nur ein Nichtterminalsymbol sein, . Damit ist jede reguläre Grammatik auch kontextfrei. Außerdem darf die rechte Seite jeder Regel ein oder mehrere Terminal- und höchstens ein Nichtterminalsymbol enthalten. Alle Regeln mit zwei Symbolen auf ihrer rechten Seite müssen die gleiche Reihenfolge von Terminal- und Nichtterminalsymbol einhalten.
Rechtsreguläre Grammatiken[Bearbeiten | Quelltext bearbeiten]
Bei rechtsregulären Grammatiken darf die rechte Seite einer Produktion nur das leere Wort, ein oder mehrere Terminalsymbole oder ein oder mehrere Terminale gefolgt von einem einzigen Nichtterminal sein. Ableitungen in solchen Grammatiken wachsen also am rechten Ende einer Satzform.
Formal kann man die Bedingung an die Produktionsmenge einer rechtsregulären Grammatik so ausdrücken:
steht dabei für das leere Wort. Dies ist gleichbedeutend mit
- .
Man beachte, dass die scheinbar strengere Anforderung
gleichmächtig ist, d. h. dieselbe formale Sprache erzeugt. Man muss nur mit Hilfe zusätzlicher Nichtterminalzeichen mehrere Regeln der Art (mit Terminalzeichen und Nichtterminalen ) hintereinander ausführen, um zu und schließlich auch zu mit einem nichtleeren Wort aus Terminalzeichen zu gelangen.[4]
Linksreguläre Grammatiken[Bearbeiten | Quelltext bearbeiten]
Bei linksregulären Grammatiken darf umgekehrt die rechte Seite einer Produktion nur das leere Wort, ein Terminalsymbol oder ein Nichtterminal gefolgt von einem Terminal sein. Hier verlängern also die Ableitungen die Satzformen linksseitig.
Formal sehen die Bedingungen folgendermaßen aus:
Erweiterte reguläre Grammatiken[Bearbeiten | Quelltext bearbeiten]
Eine erweiterte rechtsreguläre Grammatik folgt diesen Regeln:[5]
- B → a – wobei B ein Nichtterminal aus N ist, und a ein Terminal aus Σ.
- A → B – wobei A und B Nichtterminale aus N sind.
- A → wB – wobei A und B aus N und w aus Σ* ist.
- A → ε – wobei A aus N ist und ε das leere Wort.
Erweiterte linksreguläre Grammatiken sind analog zu erweiterten rechtsregulären Grammatiken.
Erweiterte reguläre Grammatiken sind gleichmächtig den streng regulären Grammatiken, d. h., sie können ebenfalls genau alle regulären Sprachen erzeugen.[5]
Weitere Schreibweisen[Bearbeiten | Quelltext bearbeiten]
Die Bedingung für reguläre Grammatiken lässt sich auch kürzer notieren, indem man die Menge der gültigen Produktionsregeln definiert:
- (rechtsregulärer Fall)
- (linksregulärer Fall)
Für beliebige und sind also im rechtsregulären Fall nur folgende Muster von Regeln erlaubt:
Für linksreguläre Grammatiken tritt anstelle des erstgenannten Musters das folgende ein:
Die jeweils erste Produktion ist rechts- beziehungsweise linksregulär (auch rechts- und linkslinear genannt). Eine reguläre Grammatik darf nicht Regeln nach beiden Mustern für 1. mischen.
Reguläre Sprachen[Bearbeiten | Quelltext bearbeiten]
Eine von einer regulären Grammatik erzeugte Sprache nennt man reguläre Sprache. Für jede reguläre Sprache existiert auch immer mindestens eine reguläre Grammatik.
Die regulären Sprachen erweisen sich als abgeschlossen unter Komplementbildung, Konkatenation, Schnitt, Vereinigung und Bildung des Kleeneschen Abschlusses.
Jede reguläre Sprache wird auch von einem geeigneten deterministischen – und dann notwendigerweise auch von einem nichtdeterministischen – endlichen Automaten akzeptiert und von einem geeigneten regulären Ausdruck beschrieben. Umgekehrt werden die Sprachen, die ein deterministischer oder nichtdeterministischer endlicher Automat akzeptiert bzw. die ein regulärer Ausdruck beschreibt, auch von einer geeigneten regulären Grammatik erzeugt. Dass in den regulären Sprachen die durch vier verschiedene Formalismen definierten Sprachklassen in einer Klasse zusammenfallen, bringt ihnen ihre große Bedeutung ein.
Auch die Klassen der rechtsregulären und der linksregulären Grammatiken fallen zusammen: Zu jeder linksregulären Grammatik gibt es eine rechtsreguläre Grammatik, die dieselbe Sprache erzeugt, und umgekehrt.
Beschreibung des Ableitungsvorgangs[Bearbeiten | Quelltext bearbeiten]
Verfolgt man den Verlauf einer Ableitung in einer rechtsregulären Grammatik, so bestehen alle Satzformen, die überhaupt noch ein Nichtterminalsymbol besitzen, aus einem Wort aus Terminalen vorneweg, gefolgt von einem einzigen Nichtterminal. Das abgeleitete Wort entsteht also schrittweise durch Anfügen eines Terminalsymbols auf der rechten Seite des initialen Terminalworts und gleichzeitiger Änderung des finalen Nichtterminals.
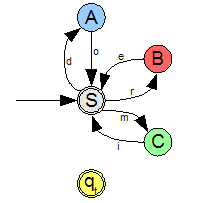
Die folgende rechtsreguläre Beispielgrammatik mit beschreibt die Sprache .
mit folgenden Regeln in :
Das Wort hat folgende Ableitung:
Dieser Prozess entspricht dem Einlesen des Wortes in einem endlichen Automaten. Es gibt einen entsprechenden Automaten, dessen Nichtterminalsymbole den Zuständen entsprechen und in dem es für jede Regel eine Transition im Automaten gibt. Der Automat zur Beispielgrammatik ist im Bild dargestellt.
Quellen und Anmerkungen[Bearbeiten | Quelltext bearbeiten]
- ↑ Lutz Engelmann (Hrsg.): Kleiner Leitfaden Informatik und ihre Anwendung. paetec, Berlin 2000, ISBN 3-89517-615-X.
- ↑ Manche Autoren bezeichnen alternativ das Quadrupel als Grammatik , oft findet man auch anderen Bezeichnungen.
- ↑ Peter Rechenberg, Gustav Pomberg (Hrsg.): Informatik-Handbuch. Hanser, München/Wien 2006, ISBN 978-3-446-40185-3.
- ↑ Sinngemäß nach Klaus Reinhardt: Prioritatszahlerautomaten und die Synchronisation von Halbspursprachen ( des vom 17. Januar 2018 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis., Fakultät Informatik der Universität Stuttgart; Doktorarbeit 1994, Seite 7
- ↑ a b Gordon Pace: Regular Languages. (PDF) In: Computability and Complexity. University of Malta, 2003, S. 22, abgerufen am 10. April 2016 (englisch).









































