Satz von König (Graphentheorie)

Der Satz von König ist ein grundlegender Satz aus dem mathematischen Gebiet der Graphentheorie, der für bipartite Graphen einen Zusammenhang zwischen einer größten Paarung und einer kleinsten Knotenüberdeckung aufzeigt. Er lautet:

In einem bipartiten Graphen ist die Größe einer größten Paarung gleich der Größe einer kleinsten Knotenüberdeckung.

Der Satz ist nach dem ungarischen Mathematiker Dénes Kőnig benannt, der ihn 1931 bewiesen hat. Er ist, wie sich zeigen lässt, als gleichwertig mit dem Hall'schen Heiratssatz aufzufassen, weswegen er auch als Satz von König–Hall (englisch König–Hall theorem) bekannt ist. Darüber hinaus hat der Mathematiker Jenő Egerváry – unabhängig von König und ebenfalls im Jahre 1931 – eine allgemeinere Fassung des Theorems für gewichtete Graphen bewiesen. Deshalb wird der Satz manchmal auch als Satz von König–Egerváry (englisch König–Egerváry theorem) bezeichnet.

Der Satz lässt sich auch auf unendliche Graphen übertragen, wie schon Paul Erdős vermutete und wie Ron Aharoni bewies.

Beispiel

Ein Beispiel eines bipartiten Graphen, mit größter Paarung (blau) und kleinster Knotenüberdeckung (rot):

Ein Beispiel eines bipartiten Graphen, mit größter Paarung (blau) und kleinster Knotenüberdeckung (rot)

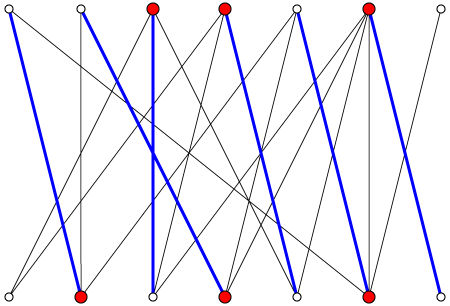
Algorithmus

Dieser Algorithmus beschreibt wie man aus einer größten Paarung die kleinste Knotenüberdeckung erhält. Eine größte Paarung kann beispielsweise mit dem Algorithmus von Hopcroft und Karp berechnet werden. Die beiden Knotenmengen des bipartiten Graphen werden in Folge mit $O$ (oben) und $U$ (unten) bezeichnet.

1. Eine größte Paarung berechnen.
2. Alle nicht in der Paarung enthaltenen Knoten aus $O$ werden in $T$ eingefügt.
3. Auf nicht in der Paarung enthaltenen Kanten gehen wir von diesen Knoten nach $U$. Alle besuchten Knoten werden in $T$ eingefügt.
4. Von den so erreichten Knoten in $U$ gehen wir auf in der Paarung enthaltenen Kanten wieder nach $O$. Alle besuchten Knoten werden in $T$ eingefügt.
5. Wiederhole die beiden vorherigen Schritte, solange bis keine neuen Knoten mehr in $T$ eingefügt werden.
6. Die kleinste Knotenüberdeckung ergibt sich aus $(O\setminus T)\cup (U\cap T)$

Variante für gewichtete Graphen

Bei der durch Jenő Egerváry (unabhängig von König) gegebenen Variante des Theorems für gewichtete Graphen betrachtet man bipartite Graphen $G=(V=A\cup B,E)$ mit einer Gewichtsfunktion $d\colon E\to \mathbb {N}$, die jeder Kante im Graphen eine nichtnegative ganze Zahl zuordnet.. Eine gewichtete Knotenüberdeckung von $d$ ist eine Funktion $\pi \colon V\to \mathbb {N}$ die jedem Knoten im Graphen eine nichtnegative ganze Zahl zuordnet, sodass $\pi (u)+\pi (v)\geq d(\{u,v\})$ für alle Kanten $\{u,v\}\in E$ gilt. Das Gewicht von $\pi$ is durch $\sum _{v\in V}\pi (v)$ gegeben. Der Satz lautet dann wie folgt:

In einem vollständigen bipartiten Graphen $G=(V=A\cup B,E)$ mit $|A|=|B|$ und einer Gewichtsfunktion $d\colon E\to \mathbb {N}$, entspricht das maximale Gewicht einer Paarung dem minimalen Gewicht einer gewichteten Knotenüberdeckung von $d$.

Version des Satzes mit binären Matrizen

Berücksichtigt man – vor dem Hintergrund des Heiratssatzes – den Zusammenhang zwischen Adjazenzmatrizen und Graphen, so gewinnt man die folgende Version des Satzes:.

In einer binären Matrix ist die minimale Anzahl von Reihen, die benötigt werden, um alle Einsen der Matrix zu erfassen, gleich der maximalen Anzahl paarweise unabhängiger Einsen.

Verwandte Sätze

• Satz von Dilworth
• Satz von Hall (Heiratssatz)
• Satz von Menger
• Satz von Birkhoff-von Neumann

Literatur

• Frank Harary: Graphentheorie. R. Oldenbourg Verlag, München, Wien 1974, ISBN 3-486-34191-X. 
• Dieter Jungnickel: Transversaltheorie (= Mathematik und ihre Anwendungen in Physik und Technik. Band 39). Akademische Verlagsgesellschaft Geest & Portig K.-G., Leipzig 1982 (MR0706076). 
• Stasys Jukna: Extremal Combinatorics (= Texts in Theoretical Computer Science). 2. Auflage. Springer-Verlag, Heidelberg, Dordrecht, London, New York 2011, ISBN 978-3-642-17363-9 (MR2865719). 
• Henryk Minc: Nonnegative Matrices (= Wiley-Interscience Series in Discrete Mathematics and Optimization). John Wiley & Sons, Inc., New York 1988, ISBN 0-471-83966-3 (MR0932967). 
• Philip F. Reichmeider: The Equivalence of Some Combinatorial Matching Theorems. Polygonal Publishing House, Washington, NJ 1984, ISBN 0-936428-09-0 (MR0781348). 
• Lutz Volkmann: Fundamente der Graphentheorie. Springer Verlag, Wien, New York 1996, ISBN 3-211-82774-9 (MR1392955). 

Weblinks

Wikiversity: Ein Beweis des Satzes von König im Rahmen eines Kurses zur diskreten Mathematik – Kursmaterialien

• Eric W. Weisstein: König-Egeváry Theorem. In: MathWorld (englisch).
• Beweis zum Satz von König (PDF; 286 kB)
• Eintrag König theorem in der Encyclopedia of Mathematics (EoM)