Benutzer:Denis~dewiki/Steinerbaumproblem
Das Steinerbaumproblem bezeichnet sowohl ein geometrisches als auch ein graphentheoretisches Problem. Beide Varianten haben gemeinsam, dass eine Menge von so genannten Terminalen mit einer kürzestmöglichen Verbindung miteinander verbunden werden soll. Sie wurden nach dem Schweizer Mathematiker Jakob Steiner benannt.
Geometrisches Steinerbaumproblem[Bearbeiten | Quelltext bearbeiten]
Ipsem lorum
Steinerbäume in Graphen[Bearbeiten | Quelltext bearbeiten]
Beim graphentheoretischen Steinerbaumproblem sucht man in einem Graphen einen kleinsten zusammenhängenden Teilgraphen (den Steinerbaum), der eine vorgegebene Menge von Endpunkten (die Terminale) enthält.
Praktische Anwendung findet die Berechnung von Steinerbäumen unter anderem beim Entwurf von integrierten Schaltkreisen[1] und von Telekommunikationsnetzen.
Definition[Bearbeiten | Quelltext bearbeiten]
Sei ein zusammenhängender, kantengewichteter Graph mit Knotenmenge und Kantenmenge . Weiterhin sei eine Menge von Terminalknoten gegeben.
Gesucht ist nun ein zusammenhängender Teilgraph, der alle Knoten aus enthält und bei dem die Summe der Kantengewichte minimal ist. Dabei können, falls nötig, auch Knoten aus verwendet werden; diese Knoten werden dann Steinerknoten oder Steinerpunkte genannt. Es ist leicht einzusehen, dass der Teilgraph ein Baum ist. Dieser wird Steinerbaum genannt.
Beziehung zu anderen Problemen[Bearbeiten | Quelltext bearbeiten]
Das Steinerbaumproblem ist eine Verallgemeinerung zweier der meistbekannten Optimierungsprobleme der Informatik:
- Wenn nur genau zwei Terminale verbunden werden sollen, sind optimale Lösungen kürzeste Pfade von nach .
- Das andere Extrem stellt der Fall dar. In diesem Fall müssen also alle Knoten miteinander verbunden werden. Man hat es damit mit dem Problem minimaler Spannbäume zu tun.
Beispiel[Bearbeiten | Quelltext bearbeiten]
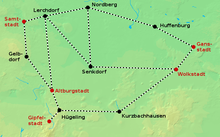
Ein Staat möchte sein marodes Schienennetz modernisieren, damit es mit Elektrolokomotiven befahren werden kann. Dafür sollen die vorhandenen Gleise mit Oberleitungen versehen werden; neue Gleise sollen nicht verlegt werden. Allerdings reicht das Budget nicht für eine Elektrifizierung des gesamten Netzes, weshalb sich die Regierung entschließt, nur so viele Strecken zu elektrifizieren, dass es möglich ist, von jeder Großstadt mit einer E-Lok in jede andere Großstadt zu fahren (dabei wird nicht ausgeschlossen, dass die E-Lok auch durch Kleinstädte fährt). Gleichzeitig sollen die Gesamtkosten für die Modernisierung möglichst gering gehalten werden. Vereinfachend wird in diesem Beispiel davon ausgegangen, dass die Kosten der Modernisierung nur von der Streckenlänge abhängen, nicht etwa von Geländebeschaffenheit usw.

Graphentheoretisch kann man das Streckennetz als Graph betrachten, bei dem die Knoten Städte repräsentieren und die Kanten vorhandene Bahnstrecken zwischen den Städten. Jeder Kante wird ein Zahlenwert (ihr Gewicht) zugewiesen, der der Streckenlänge entspricht. Man kann nun die zu verbindenden Großstädte als Terminale auffassen. Die Aufgabe ist somit, eine gewichtsminimale Teilmenge der Kanten zu finden, die alle Terminale verbindet; sprich: ein Oberleitungsnetz zu finden, das alle Großstädte verbindet und dabei so kostengünstig wie möglich ist. Die Suche nach dieser Teilmenge entspricht der Suche nach einem Steinerbaum.
Der rechts abgebildete Steinerbaum repräsentiert all die Strecken, die elektrifiziert werden müssen, um alle Großstädte zu verbinden. Hierfür sind in diesem Beispiel 190 km Oberleitung nötig; mit weniger Leitung ist die Zielsetzung nicht zu erreichen.
Während es bei diesem Beispiel noch relativ leicht ist, den Steinerbaum zu finden, ist es für größere Schienennetze mit mehr Städten für Computer ebenso wie für Menschen praktisch unmöglich, eine optimale Lösung zu finden.
Geschichte[Bearbeiten | Quelltext bearbeiten]
Komplexität[Bearbeiten | Quelltext bearbeiten]
Die kanonische Entscheidungsvarinte des Steinerbaumproblems in Graphen gehört zu den 21 klassischen Problemen, deren NP-Vollständigkeit 1972 von Richard M. Karp nachgewiesen wurde. Es kann also keinen Algorithmus für das Steinerbaumproblem mit polynomieller Laufzeit geben, außer wenn P = NP gilt. Da in polynomieller Zeit der Wert eines Steinerbaums (das Gewicht all seiner Kanten) bestimmt werden kann, folgt aus der NP-Vollständigkeit der Entscheidungsvariante auch die NP-Schwere des Steinerbaumproblems selbst.
Das Problem bleibt sogar dann NP-schwer, wenn man die Graphen auf quasi-bipartite Graphen einschränkt. Ein Graph heißt dabei quasi-bipartit, wenn keine zwei Terminale oder zwei Nicht-Terminale mit einer Kante verbunden sind. Auch wenn man das Problem auf ungewichtete Graphen einschränkt, bleibt es NP-schwer [2].
Mit Hilfe eines Enumerationsalgorithmus ist die Berechnung eines minimalen Steinerbaumes in polynomieller Zeit möglich, falls die Zahl der Nicht-Terminale beschränkt ist, d.h. falls man sich auf Instanzen beschränkt, bei denen für ein vorgegebenes k nicht mehr als k Nicht-Terminale enthalten sind. Ein Spezialfall ist hier k=0, der mit der Suche nach einem minimalen Spannbaum identisch ist.
Der Dreyfus-Wagner-Algorithmus liefert einen minimalen Steinerbaum in polynomieller Zeit, falls die Zahl der Terminale beschränkt ist, d.h. falls man sich auf Instanzen beschränkt, bei denen für ein vorgegebenes k nicht mehr als k Terminale enthalten sind. Ein Spezialfall ist hier k=2, der mit der Suche nach einem kürzesten Pfad identisch ist.
Approximierbarkeit[Bearbeiten | Quelltext bearbeiten]
Wegen der NP-Schwere des Problems ist es sinnvoll, Methoden zu untersuchen, welche durch Approximation nach Lösungen zu suchen, die nicht notwendigerweise optimal sind, dafür aber relativ gute Lösungswerte haben.
Falls P ungleich NP ist (siehe P-NP-Problem), so gibt es auch keine polynomiellen Algorithmen, die beliebig gute approximative Lösungen liefern (PAS).[3]
Die Approximationsalgorithmen mit der besten bekannten Approximationsgüte sind der relative Greedy-Algorithmus (Approximationsgüte ) und der Loss-Kontraktions-Algorithmus (Approximationsgüte [4]). Für beide Algorithmen wird vermutet, dass ihre Analyse bisher nicht bestmöglich ist. Insofern ist nicht klar, ob der relative Greedy-Algorithmus nicht doch besser als der Loss-Kontraktions-Algorithmus approximiert. Beide Algorithmen versuchen sogenannte k-Steinerbäume zu approximieren. Streng genommen handelt es sich bei beiden Algorithmen um Approximationsschemata, also eine Menge von Algorithmen, deren Approximationsgüte sich wenigstens den genannten Werten nähert. Ihre Laufzeit ist für reale Anwendungen allerdings unbrauchbar.
Effizientere Approximationsalgorithmen[Bearbeiten | Quelltext bearbeiten]
Der Algorithmus von Kou, Markowsky und Berman erreicht Approximationsgüte 2 und ist mit Laufzeit O(|V|² · log|V| + |V| · |E|) wesentlich schneller als der relative Greedy-Algorithmus oder der Loss-Kontraktions-Algorithmus. Er berechnet dazu einen Distanzgraphen und darauf einen minimalen Spannbaum. Die Berechnung des Distanzgraphen bestimmt im Wesentlichen die Laufzeit des Algorithmus. Der Algorithmus von Mehlhorn verbessert diese Laufzeit auf O(|V| · log|V| + |E|), indem er statt eines vollständigen nur einen modifizierten Distanzgraphen berechnet[5]. Auch der Algorithmus von Mehlhorn erreicht Approximationsgüte 2. Die Analyse der Algorithmen von Kou-Markowsky-Berman bzw. Mehlhorn ist bestmöglich.
Komplexität spezieller Varianten[Bearbeiten | Quelltext bearbeiten]
Wie bei vielen anderen schweren Problemen der theoretischen Informatik gibt es auch für das Steinerbaumproblem zahlreiche einschränkende Varianten. Hierbei versucht man, durch Einschränkungen und Nebenbedingungen den Suchraum des Problems drastisch zu verkleinern und somit die Berechnung einer Lösung stark zu beschleunigen.
Das Steinerbaumproblem bleibt jedoch weiterhin NP-vollständig, wenn man sich auf bipartite ungewichtete Graphen beschränkt. Auch bei Beschränkung auf metrische Graphen bleibt das Problem noch NP-vollständig.
Oft wird das metrische Steinerbaumproblem auch so verallgemeinert, dass die Menge der Knoten unendlich ist, zum Beispiel wird bei vielen Problemstellungen die Ebene als Knotenmenge betrachtet. Die Knoten sind dann paarweise durch eine Kante entsprechend der verwendeten Metrik verbunden. Lediglich die Zahl der Terminale bleibt dann weiter endlich. Für euklidische Metriken oder die Manhattan-Metrik, die in praktischen Anwendungen relativ häufig gegeben sind, existieren polynomielle Approximationsschemata, so dass sich selbst für mehrere Tausend Knoten gute Lösungen des Problems finden lassen.
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ C. Chiang, M. Sarrafzadeh, C. K. Wong: Global Routing Based on Steiner Min-Max Trees. In: IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems. Band 9, Nr. 12, 2006, ISSN 0278-0070, S. 1318–1325, doi:10.1109/43.62776.
- ↑ Marshall W. Bern, Paul E. Plassmann: The Steiner Problem with Edge Lengths 1 and 2. In: Information Processing Letters. Band 32, Nr. 4, 1989, S. 171–176, doi:10.1016/0020-0190(89)90039-2.
- ↑ Clemens Gröpl, Stefan Hougardy, Till Nierhoff, Hans Jürgen Prömel: Lower Bounds for Approximation Algorithms for the Steiner Tree Problem. In: Proceedings of the 27th International Workshop on Graph-Theoretic Concepts in Computer Science (= Lecture Notes in Computer Science). Band 2204, 2001, ISBN 3-540-42707-4, ISSN 0302-9743, S. 217–228, doi:10.1007/3-540-45477-2_20 (http://www.inf.fu-berlin.de/inst/ag-bio/FILES/ROOT/Publications/groepl/GHNP01b.ps PS, 239 kB).
- ↑ Gabriel Robins, Alexander Zelikovsky: Improved Steiner Tree Approximation in Graphs. In: Proceedings of the Eleventh Annual ACM-SIAM Symposium on Discrete Algorithms. 2000, S. 770–779 (http://www.cs.virginia.edu/~robins/papers/soda2000_camera.pdf PDF, 260 kB).
- ↑ Kurt Mehlhorn: A Faster Approximation Algorithm for the Steiner Problem in Graphs. In: Information Processing Letters. Band 27, Nr. 2, 1988, S. 125–128, doi:10.1016/0020-0190(88)90066-X.
Literatur[Bearbeiten | Quelltext bearbeiten]
- F. K. Hwang, D. S. Richards, P. Winter: The Steiner Tree Problem. Elsevier, 1992, ISBN 0-08-086793-6 (englisch).
- Hans Jürgen Prömel, Angelika Steger: The Steiner Tree Problem. A Tour Through Graphs, Algorithms, and Complexity. Vieweg, 2002, ISBN 3-528-06762-4 (englisch).











