Eulerkreisproblem

Ein Eulerkreis (auch geschlossener Eulerzug, Eulertour) ist in der Graphentheorie ein Zyklus, der alle Kanten eines Graphen genau einmal enthält.
Ein offener Eulerzug (auch Eulerpfad oder Eulerweg) ist gegeben, wenn Start- und Endknoten nicht gleich sein müssen, wenn also statt eines Zyklus lediglich eine Kantenfolge verlangt wird, welche jede Kante des Graphen genau einmal enthält. Ein bekanntes Beispiel ist das „Haus vom Nikolaus“.
Ein zusammenhängender Graph, der einen Eulerkreis besitzt, heißt eulerscher Graph. Enthält ein Graph lediglich einen Eulerweg und keinen Eulerkreis, so heißt er semi-eulerscher Graph. Die Aufgabe, zu einem gegebenen Graph zu bestimmen, ob dieser eulersch ist oder nicht, wird als Eulerkreisproblem bezeichnet. Es geht auf das 1736 von Leonhard Euler gelöste Königsberger Brückenproblem zurück. Das Problem existiert auch für gerichtete Graphen und Graphen mit Mehrfachkanten.
Entgegen seinem Namen ist der Eulerkreis kein Kreis, zumindest wenn der häufigen Definition gefolgt wird, nach der sich in einem Kreis kein Knoten wiederholen darf.
Geschichte[Bearbeiten | Quelltext bearbeiten]
Leonhard Euler fragte in seiner Arbeit 1736 zum Königsberger Brückenproblem – übersetzt in die heutige Fachsprache –, ob der durch die Brücken der Stadt gegebene Graph ein semi-eulerscher Graph ist, das heißt, ob ein Eulerweg existiert, und verneinte dies, da der Graph mehr als zwei Knoten mit ungeradem Grad hatte. Euler bewies, dass ein semi-eulerscher Graph höchstens zwei Knoten ungeraden Grades haben kann.[1] Er vermutete und gab ohne Beweis an, dass dies eine hinreichende Bedingung sei: Ein zusammenhängender Graph, in dem jeder Knoten geraden Grad hat, ist ein Eulergraph. Ein Beweis des Satzes wurde zuerst von Carl Hierholzer 1873 veröffentlicht.[2] Auf dem Beweis basiert der Algorithmus von Hierholzer zum Auffinden eines Eulerwegs.
Charakterisierung[Bearbeiten | Quelltext bearbeiten]
Nach dem Satz von Euler-Hierholzer sind eulersche Graphen leicht zu charakterisieren.
Sei G ein Graph, bei dem höchstens eine Zusammenhangskomponente Kanten enthält. Dann sind folgende Aussagen äquivalent:
- G ist eulersch,
- jeder Knoten in G hat geraden Grad.
- die Kantenmenge von G ist die Vereinigungsmenge aller Kanten von paarweise disjunkten Kreisen.
Analog sind für einen gerichteten Graphen G, bei dem höchstens eine starke Zusammenhangskomponente Kanten enthält, folgende Aussagen äquivalent:
- G ist eulersch,
- für jeden Knoten in G sind Eingangsgrad und Ausgangsgrad gleich.
- die Kantenmenge von G ist die Vereinigungsmenge aller Kanten von paarweise disjunkten gerichteten Kreisen.
Verallgemeinerung: Eulerweg[Bearbeiten | Quelltext bearbeiten]
Ein ungerichteter zusammenhängender Graph enthält genau dann einen Eulerweg, wenn zwei oder keiner seiner Knoten von ungeradem Grad sind. Hat kein Knoten einen ungeraden Grad, handelt es sich bei jedem Eulerweg um einen Eulerkreis.
Entscheidungsproblem[Bearbeiten | Quelltext bearbeiten]
Die Frage, ob für einen gegebenen Graph ein Eulerkreis existiert, lässt sich algorithmisch relativ leicht lösen, da ein Graph genau dann eulersch ist, wenn er zusammenhängend ist und jeder Knoten geraden Grad besitzt. Mittels Tiefensuche lässt sich dies leicht in linearer Zeit feststellen.
Auffinden eines Eulerkreises[Bearbeiten | Quelltext bearbeiten]
Zum Auffinden eines Eulerkreises existieren mehrere Verfahren. Der Algorithmus von Fleury stammt aus dem Jahr 1883 und verfolgt einen sehr einfachen Ansatz, weshalb er eine Laufzeit von der Größenordnung hat. Effizienter ist der Algorithmus von Hierholzer, der einen Eulerkreis in Linearzeit berechnet. Er basiert darauf, dass sich ein eulerscher Graph in paarweise kantendisjunkte Kreise zerlegen lässt.
Algorithmus von Hierholzer[Bearbeiten | Quelltext bearbeiten]
- Wähle einen beliebigen Knoten des Graphen und konstruiere von ausgehend einen Kreis in , der keine Kante in zweimal durchläuft.
- Wenn ein Eulerkreis ist, brich ab. Andernfalls:
- Vernachlässige nun alle Kanten des Kreises .
- Am ersten Knoten von , dessen Grad größer 0 ist, wird nun ein weiterer Kreis gebildet, der keine Kante in durchläuft und keine Kante in zweimal enthält.
- Füge in den zweiten Kreis ein, indem der Startknoten von durch alle Knoten von in der richtigen Reihenfolge ersetzt wird.
- Nenne jetzt den so erhaltenen Kreis und fahre bei Schritt 2 fort.
Die Laufzeit des Algorithmus ist linear in der Anzahl der Kanten, ist also von der Größenordnung .
Beispiel[Bearbeiten | Quelltext bearbeiten]

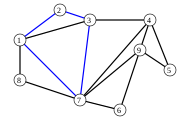
Gegeben sei ein Eulergraph mit neun Knoten (siehe erste Abbildung). Ein Zyklus vom Startknoten 1 wäre beispielsweise die in der zweiten Abbildung blau dargestellte Knotenfolge . Nach Entfernen dieser Kanten haben die Knoten 1, 3 und 7 der bisher gebildeten Zyklus noch einen Knotengrad größer Null, welche als Startknoten für den nächsten Zyklus in Frage kommen. Vom Startknoten 3 aus kann man den Kreis bilden (siehe dritte Abbildung). Wählt man nun als Startknoten den Knoten 7, kann man von den übrig gebliebenen Kanten den Zyklus bilden. Setzt man jetzt in an Stelle des Knoten 7 ein, erhält man den Zyklus . Setzt man diesen in an Stelle des Knoten 3 ein, erhält man die mögliche Eulertour wie in der letzten Abbildung gezeigt.
Die Abbildung rechts zeigt eine Animation für dieses Beispiel.
-
Eulergraph mit neun Knoten
-
-
Nach Entfernen der blauen Kanten kann man den nächsten Zyklus ausgehend vom Knoten 1, 3 oder 7 bilden, hier vom Knoten 3:
-
Nach Entfernen der roten Kanten kann man den nächsten Zyklus ausgehend vom Knoten 4 oder 7 bilden, hier vom Knoten 7:
-
Eulerkreis mit der Knotenfolge
Programmierung[Bearbeiten | Quelltext bearbeiten]
Das folgende Beispiel in der Programmiersprache C# zeigt die Implementierung des Algorithmus von Hierholzer für einen ungerichteten Graphen. Bei der Ausführung des Programms wird die Methode Main verwendet, die den Eulerkreis auf der Konsole ausgibt.[3]
| Code-Schnipsel |
using System;
using System.Collections.Generic;
// Deklariert die Klasse für die Knoten des Graphen
class Node
{
public int index;
public string value;
public HashSet<Node> adjacentNodes = new HashSet<Node>(); // Menge der Nachbarknoten
}
// Deklariert die Klasse für den ungerichteten Graphen
class UndirectedGraph
{
// Diese Methode verbindet die Knoten node1 und node2 miteinander.
public void ConnectNodes(Node node1, Node node2)
{
node1.adjacentNodes.Add(node2);
node2.adjacentNodes.Add(node1);
}
// Diese Methode trennt die Knoten node1 und node2 voneinander.
public void DisconnectNodes(Node node1, Node node2)
{
node1.adjacentNodes.Remove(node2);
node2.adjacentNodes.Remove(node1);
}
}
class Program
{
// Diese Methode gibt den Eulerkreis, die als Liste von Knoten übergeben wird, in der Form (A, B), (B, C), (C, D), ... als Text zurück.
public static string EulerCircuitToString(List<Node> nodeList)
{
string text = "";
for (int i = 0; i < nodeList.Count - 1; i++) // for-Schleife, die die Knoten durchläuft
{
text += "(" + nodeList[i].value + ", " + nodeList[i + 1].value + "), ";
}
text = text.Substring(0, text.Length - 2);
return text;
}
// Diese Methode gibt die Liste der durchlaufenen Knoten zurück
public static List<Node> GetEulerCircuitByHierholzer(UndirectedGraph undirectedGraph, Node startNode)
{
List<Node> nodeList = new List<Node>(); // Initialisiert die Liste der durchlaufenen Knoten
Stack<Node> currentPath = new Stack<Node>(); // Initialisiert einen Stapelspeicher für die hinzugefügten Knoten
currentPath.Push(startNode); // Fügt den Startknoten dem Stapelspeicher hinzu
Node currentNode = startNode; // Setzt den Startknoten
while (currentPath.Count != 0) // So lange der Stapelspeicher für die hinzugefügten Knoten nicht leer ist
{
if (currentNode.adjacentNodes.Count != 0) // Wenn noch nicht alle anliegenden Kanten des aktuellen Knotens durchlaufen wurden
{
currentPath.Push(currentNode); // Fügt den aktuellen Knoten dem Stapelspeicher hinzu
HashSet<Node>.Enumerator enumerator = currentNode.adjacentNodes.GetEnumerator();
enumerator.MoveNext();
Node nextNode = enumerator.Current; // Setzt den nächsten Knoten auf einen Nachbarknoten des aktuellen Knotens
undirectedGraph.DisconnectNodes(currentNode, nextNode); // Löscht die Kante zwischen aktuellem Knoten und Nachbarknoten
currentNode = nextNode; // Setzt den aktuellen Knoten auf den Nachbarknoten
}
else // Sonst Backtracking verwenden, um einen weiteren Kreis zu finden
{
nodeList.Insert(0, currentNode); // Fügt den aktuellen Knoten am Anfang der Liste der durchlaufenen Knoten ein
currentNode = currentPath.Pop(); // Löscht das oberste Element, also den letzten Knoten vom Stapelspeicher
}
}
return nodeList;
}
// Hauptmethode, die das Programm ausführt
public static void Main()
{
// Deklariert und initialisiert 7 Knoten
Node node1 = new Node{index = 0, value = "A"};
Node node2 = new Node{index = 1, value = "B"};
Node node3 = new Node{index = 2, value = "C"};
Node node4 = new Node{index = 3, value = "D"};
Node node5 = new Node{index = 4, value = "E"};
Node node6 = new Node{index = 5, value = "F"};
Node node7 = new Node{index = 6, value = "G"};
// Erzeugt einen ungerichteten Graphen
UndirectedGraph undirectedGraph = new UndirectedGraph();
// Verbindet Knoten des Graphen miteinander
undirectedGraph.ConnectNodes(node1, node2);
undirectedGraph.ConnectNodes(node1, node7);
undirectedGraph.ConnectNodes(node2, node3);
undirectedGraph.ConnectNodes(node3, node1);
undirectedGraph.ConnectNodes(node3, node4);
undirectedGraph.ConnectNodes(node4, node5);
undirectedGraph.ConnectNodes(node5, node3);
undirectedGraph.ConnectNodes(node5, node6);
undirectedGraph.ConnectNodes(node6, node1);
undirectedGraph.ConnectNodes(node7, node5);
List<Node> eulerCircuit = GetEulerCircuitByHierholzer(undirectedGraph, node1); // Aufruf der Methode, die die Liste der durchlaufenen Knoten zurückgibt
if (eulerCircuit.Count == 11) // Wenn die Anzahl der durchlaufenen Knoten um 1 größer als die Anzahl aller Kanten ist
{
string eulerCircuitText = EulerCircuitToString(eulerCircuit); // Aufruf der Methode
Console.WriteLine(eulerCircuitText); // Ausgabe auf der Konsole
}
else
{
Console.WriteLine("Es existiert kein Eulerkreis."); // Ausgabe auf der Konsole
}
Console.ReadLine();
}
}
|
Hinweise: In der Methode GetEulerCircuitByHierholzer werden die Knoten des Eulerkreises in einer Liste gespeichert. Die Knoten des aktuell durchlaufenen Kreises werden in einem Stack (Stapelspeicher) gespeichert. Wenn kein Nachbarknoten des aktuell durchlaufenen Knoten erreichbar ist, weil alle Kanten dieses Knotens gelöscht wurden, wird der zuletzt durchlaufene Knoten vom Stack genommen und am Anfang der Liste eingefügt. Dabei wird Backtracking ohne rekursive Programmierung verwendet.
Im Programmbeispiel wird nur einer der möglichen Eulerkreise bestimmt und ausgegeben.[3]
Algorithmus von Fleury[Bearbeiten | Quelltext bearbeiten]
Im Algorithmus von Fleury spielen Brückenkanten eine wichtige Rolle. Das sind Kanten, ohne die der Graph in zwei Komponenten zerfallen würde.
Der Algorithmus fügt einer anfangs leeren Kantenfolge alle Kanten eines Graphen hinzu, sodass ein Eulerkreis entsteht.
- Wähle einen beliebigen Knoten als aktuellen Knoten.
- Wähle unter den unmarkierten, mit dem aktuellen Knoten inzidenten Kanten eine beliebige Kante aus. Dabei sind zuerst Kanten zu wählen, die im unmarkierten Graphen keine Brückenkanten sind.
- Markiere die gewählte Kante und füge sie der Kantenfolge hinzu.
- Wähle den anderen Knoten der gewählten Kante als neuen aktuellen Knoten.
- Wenn noch unmarkierte Kanten existieren, dann gehe zu Schritt 2.
Ob eine Kante eine Brückenkante ist, kann mittels Tiefensuche in Laufzeit überprüft werden. Da pro Schritt eine Kante entfernt wird, werden Iterationen benötigt. Die Anzahl der pro Iteration geprüften Kanten entspricht dem Grad des aktuellen Knotens. Insgesamt kann die gesamte Anzahl überprüfter Kanten durch beschränkt werden. Die gesamte Laufzeit ist damit von der Größenordnung .
Programmierung[Bearbeiten | Quelltext bearbeiten]
Das folgende Beispiel in der Programmiersprache C# zeigt die Implementierung des Algorithmus von Fleury für einen ungerichteten Graphen. Der ungerichtete Graph wird als Klasse UndirectedGraph deklariert. Bei der Ausführung des Programms wird die Methode Main verwendet, die den Eulerkreis oder Eulerpfad auf der Konsole ausgibt.[4]
| Code-Schnipsel |
using System;
using System.Collections.Generic;
// Deklariert die Klasse für die Knoten des Graphen
class Node
{
public int index;
public string value;
public HashSet<Node> adjacentNodes = new HashSet<Node>(); // Menge der Nachbarknoten
}
// Deklariert die Klasse für den ungerichteten Graphen
class UndirectedGraph
{
public HashSet<Node> nodes = new HashSet<Node>();
// Diese Methode verbindet die Knoten node1 und node2 miteinander.
public void ConnectNodes(Node node1, Node node2)
{
node1.adjacentNodes.Add(node2);
node2.adjacentNodes.Add(node1);
}
// Diese Methode trennt die Knoten node1 und node2 voneinander.
public void DisconnectNodes(Node node1, Node node2)
{
node1.adjacentNodes.Remove(node2);
node2.adjacentNodes.Remove(node1);
}
}
class Program
{
// Diese Methode gibt die Eulerpfad, die als Liste von Knoten übergeben wird, in der Form (A, B), (B, C), (C, D), ... als Text zurück.
public static string EulerPathToString(List<Node> nodeList)
{
string text = "";
for (int i = 0; i < nodeList.Count - 1; i++) // for-Schleife, die die Knoten durchläuft
{
text += "(" + nodeList[i].value + ", " + nodeList[i + 1].value + "), ";
}
text = text.Substring(0, text.Length - 2);
return text;
}
// Diese Methode gibt die Liste der durchlaufenen Knoten zurück
public static List<Node> GetEulerPathByFleury(UndirectedGraph undirectedGraph, Node startNode)
{
// Behandelt den Fall, dass es zwei Knoten mit ungeradem Grad gibt und sucht einen Knoten mit ungeradem Grad
foreach (Node node in undirectedGraph.nodes) // foreach-Schleife, die alle Knoten des Graphen durchläuft
{
if (node.adjacentNodes.Count % 2 == 1) // Wenn der Grad des aktuellen Knoten ungerade ist
{
startNode = node; // Knoten als Startknoten auswählen und foreach-Schleife verlassen
break;
}
}
List<Node> nodeList = new List<Node>(); // Initialisiert die Liste der durchlaufenen Knoten
Node nextNode = null; // Referenz auf den jeweils nächsten Knoten der Eulerpfad, die gegebenenfalls nach dem vollständigen Durchlaufen der Kanten für den letzten Knoten (Zielknoten) benötigt wird.
AddNextEulerPathNode(undirectedGraph, startNode, ref nextNode, nodeList); // Aufruf der rekursiven Methode, die jeweils den nächsten Knoten hinzufügt
if (nextNode != null)
{
nodeList.Add(nextNode); // Wenn Referenz nicht null, Zielknoten hinzufügen
}
return nodeList;
}
// Rekursive Methode, die jeweils den nächsten Knoten hinzufügt
private static void AddNextEulerPathNode(UndirectedGraph undirectedGraph, Node startNode, ref Node nextNode, List<Node> nodeList)
{
HashSet<Node> adjacentNodes = new HashSet<Node>(startNode.adjacentNodes);
foreach (Node node in adjacentNodes)
{
if (startNode.adjacentNodes.Contains(node) && IsValidNextEdge(undirectedGraph, startNode, node))
{
nextNode = node;
nodeList.Add(startNode);
undirectedGraph.DisconnectNodes(startNode, node);
AddNextEulerPathNode(undirectedGraph, node, ref nextNode, nodeList); // Rekursiver Aufruf der Methode
}
}
}
// Diese Methode prüft, ob sich mit der aktuellen Kante die Eulerpfad vervollständigen lässt
private static bool IsValidNextEdge(UndirectedGraph undirectedGraph, Node node1, Node node2)
{
if (node1.adjacentNodes.Count == 1 && node1.adjacentNodes.Contains(node2))
{
return true;
}
HashSet<Node> visitedNodes = new HashSet<Node>();
DepthFirstSearch(node1, visitedNodes);
int count1 = visitedNodes.Count;
undirectedGraph.DisconnectNodes(node1, node2);
visitedNodes.Clear();
DepthFirstSearch(node1, visitedNodes);
int count2 = visitedNodes.Count;
undirectedGraph.ConnectNodes(node1, node2);
return count1 == count2;
}
// Diese Methode verwendet Tiefensuche, um alle erreichbaren Knoten des Graphen zu durchlaufen
private static void DepthFirstSearch(Node startNode, HashSet<Node> visitedNodes)
{
visitedNodes.Add(startNode); // Fügt den aktuellen Knoten der Menge der markierten Knoten hinzu
foreach (Node node in startNode.adjacentNodes) // foreach-Schleife, die alle benachbarten Knoten des Knotens durchläuft
{
if (!visitedNodes.Contains(node)) // Wenn der Knoten noch nicht markiert wurde
{
DepthFirstSearch(node, visitedNodes); // Rekursiver Aufruf der Methode mit dem Nachbarknoten als Startknoten
}
}
}
// Hauptmethode, die das Programm ausführt
public static void Main()
{
// Deklariert und initialisiert 5 Knoten
Node node1 = new Node{index = 0, value = "A"};
Node node2 = new Node{index = 1, value = "B"};
Node node3 = new Node{index = 2, value = "C"};
Node node4 = new Node{index = 3, value = "D"};
Node node5 = new Node{index = 4, value = "E"};
// Deklariert und initialisiert ein Array mit den Knoten
Node[] nodes = {node1, node2, node3, node4, node5};
// Erzeugt einen ungerichteten Graphen
UndirectedGraph undirectedGraph = new UndirectedGraph();
int numberOfNodes = nodes.Length;
for (int i = 0; i < numberOfNodes; i++) // for-Schleife, die alle Knoten durchläuft
{
undirectedGraph.nodes.Add(nodes[i]); // Fügt die Knoten dem Graphen hinzu
}
// Verbindet Knoten des Graphen miteinander
undirectedGraph.ConnectNodes(node2, node1);
undirectedGraph.ConnectNodes(node1, node3);
undirectedGraph.ConnectNodes(node3, node2);
undirectedGraph.ConnectNodes(node1, node4);
undirectedGraph.ConnectNodes(node4, node5);
undirectedGraph.ConnectNodes(node4, node3);
undirectedGraph.ConnectNodes(node4, node2);
undirectedGraph.ConnectNodes(node3, node5);
List<Node> eulerPath = GetEulerPathByFleury(undirectedGraph, node1); // Aufruf der Methode, die die Liste der durchlaufenen Knoten zurückgibt
if (eulerPath.Count == 9) // Wenn die Anzahl der durchlaufenen Knoten um 1 größer als die Anzahl aller Kanten ist
{
string eulerPathText = EulerPathToString(eulerPath); // Aufruf der Methode
Console.WriteLine(eulerPathText); // Ausgabe auf der Konsole
}
else
{
Console.WriteLine("Es existiert kein Eulerpfad."); // Ausgabe auf der Konsole
}
Console.ReadLine();
}
}
|
Hinweise: Sowohl für das Referenzieren der Knoten des ungerichteten Graphen als auch für das Referenzieren der Nachbarknoten jedes Knoten wird ein HashSet (Menge) als Datentyp verwendet und mit foreach-Schleifen durchlaufen. Der Vorteil des HashSet für die Nachbarknoten im Vergleich zu einer Liste ist, dass dann meist viel schneller, nämlich mit konstanter Laufzeit, geprüft werden kann, ob ein bestimmter Knoten Nachbarknoten eines anderen Knoten ist (siehe Hashtabelle – Vorteile). Ein Nachteil ist, dass dann die Reihenfolge der durchlaufenen Knoten in den foreach-Schleifen und damit auch die Reihenfolge der ausgegebenen Knoten des Eulerpfads nicht eindeutig oder teilweise zufällig ist.
Im Programmbeispiel wird nur einer der möglichen Eulerpfade bestimmt und ausgegeben, falls einer existiert.
Statt dem HashSet (Menge) visitedNodes kann auch eine Liste oder ein Array vom Typ bool (Boolesche Variable) verwendet werden, wie im Einzelnachweis gezeigt.[4]
Vermutung von Hajos[Bearbeiten | Quelltext bearbeiten]
Nach der im Allgemeinen ungelösten Zyklenvermutung von György Hajós über Kreiszerlegung von Eulergraphen von 1968 können Eulergraphen mit Knoten in höchstens Kreise zerlegt werden. Die Vermutung wurde für kleine Graphen () 2017 bewiesen[5] und für Pfadweite kleiner oder gleich 6.[6]
Anwendungsbeispiele[Bearbeiten | Quelltext bearbeiten]
Das Königsberger Brückenproblem[Bearbeiten | Quelltext bearbeiten]
Das Königsberger Brückenproblem lässt sich in folgendem Graphen ausdrücken:

Die Kreise (Knoten) sind die jeweiligen Stadtteile bzw. Standpunkte. Die Linien (Kanten) sind die Brücken. Durch Probieren wird herausgefunden, dass es nicht möglich ist, einen Rundgang durch die Stadt zu finden, bei dem jede Brücke genau ein einziges Mal benutzt wird. Es gibt also keinen Eulerweg und demzufolge auch keinen Eulerkreis. Warum ist das so?
Euler hat die folgende Gesetzmäßigkeit entdeckt: Wenn in einem Graphen G ein Eulerweg existiert, dann haben maximal 2 Knoten ungeraden Grad. Beim Königsberger Brückengraphen gibt es vier Knoten mit ungeradem Grad. Die Zahlen neben den Knoten geben in der Abbildung deren Grad an. Deshalb ist der Stadtrundgang mit dem nur einmaligen Benutzen jeder Brücke unmöglich.
Ein ungerader Knoten ist entweder Anfang oder Ende des Weges über die Brücken: null ungerade Knoten würde bedeuten, dass Anfang und Ende des Weges in Königsberg identisch sind. Ein Weg mit Anfang und Ende hätte maximal zwei ungerade Knoten. Ergo ist es in Königsberg nicht möglich gewesen, alle Brücken in einem Wege nur jeweils einmal zu begehen.
Das Haus vom Nikolaus[Bearbeiten | Quelltext bearbeiten]
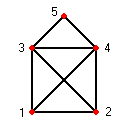
Das beliebte Kinderrätsel „Das ist das Haus vom Nikolaus“ hingegen enthält einen Eulerweg, aber keinen Eulerkreis, da sein Graph zwei Knoten vom Grad 3 enthält.
Solch ein Eulerweg ist 1-2-4-3-1-4-5-3-2. Knoten 1 und 2 haben jeweils 3 Nachbarn, ihr Grad ist also ungerade. Um das Haus in einem Zug zeichnen zu können, muss daher an einem dieser beiden Punkte begonnen werden. Ein Quadrat mit Diagonalen enthält keinen Eulerweg, da alle seine Knoten den Grad 3 haben. Im Bild sind das nur die Punkte 1, 2, 3, 4 mit den verbindenden Kanten.
Siehe auch[Bearbeiten | Quelltext bearbeiten]
Literatur[Bearbeiten | Quelltext bearbeiten]
- Wladimir Velminski: Leonhard Euler. Die Geburt der Graphentheorie. Kulturverlag Kadmos, Berlin 2008, ISBN 978-3-86599-056-3.
- Reinhard Diestel: Graphentheorie. 3. Auflage. Springer, 2006, ISBN 3-540-21391-0, S. 23–24
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Brian Hopkins, Robin J. Wilson: The Truth about Königsberg. In: The College Mathematics Journal. Band 35, Nr. 3, 2004, Paragraphen 20 und 21, doi:10.1080/07468342.2004.11922073.
- ↑ Hierholzer Über die Möglichkeit, einen Linienzug ohne Wiederholung und ohne Unterbrechung zu umfahren, Mathematische Annalen, Bd. 6, 1873, S. 30–32, Online
- ↑ a b GeeksforGeeks: Hierholzer’s Algorithm for directed graph
- ↑ a b GeeksforGeeks: Fleury’s Algorithm for printing Eulerian Path or Circuit
- ↑ Irene Heinrich, Marco Natale, Manuel Streicher, Hajós' cycle conjecture for small graphs, Arxiv 2017
- ↑ Elke Fuchs, Laura Gellert, Irene Heinrich: Cycle decompositions of pathwidth-6 graphs, Arxiv 2017