Hashtabelle
In der Informatik bezeichnet man eine spezielle Indexstruktur als Hashtabelle (englisch hash table oder hash map) bzw. Streuwerttabelle. Sie wird verwendet, um Datenelemente in einer großen Datenmenge zu suchen bzw. aufzufinden (Hash- oder Streuspeicherverfahren).
Gegenüber alternativen Index-Datenstrukturen wie Baumstrukturen (z. B. ein B+-Baum) oder Skip-Listen zeichnen sich Hashtabellen üblicherweise durch einen konstanten Zeitaufwand bei Einfüge- bzw. Entfernen-Operationen aus.
Hashverfahren[Bearbeiten | Quelltext bearbeiten]
Das Hashverfahren ist ein Algorithmus zum Suchen von Datenobjekten in großen Datenmengen. Es basiert auf der Idee, dass eine mathematische Funktion, die Hashfunktion, die Position eines Objektes in einer Tabelle berechnet. Dadurch erübrigt sich das Durchsuchen vieler Datenobjekte, bis das Zielobjekt gefunden wurde.
Der Algorithmus[Bearbeiten | Quelltext bearbeiten]
Beim Hashverfahren werden die Zieldaten in einer Hashtabelle gespeichert. Dabei dient nicht der Schlüssel, der das Datenobjekt eindeutig identifiziert, als Index, sondern der Hashwert, der von einer Hashfunktion aus dem Schlüssel berechnet wird. Der durch den Hashwert festgelegte Speicherort eines Datenobjektes in der Tabelle wird auch als Bucket bezeichnet (englisch Behälter).
Im Idealfall bekommt jedes Objekt einen eigenen Bucket (d. h. keine Kollisionen, s. u.).
In der Praxis wird die Tabelle als ein Array implementiert.
Kollisionen[Bearbeiten | Quelltext bearbeiten]
Da Hashfunktionen im Allgemeinen nicht eindeutig (injektiv) sind, können zwei unterschiedliche Schlüssel zum selben Hash-Wert, also zum selben Feld in der Tabelle, führen. Dieses Ereignis wird als Kollision bezeichnet. In diesem Fall muss die Hashtabelle mehrere Werte an derselben Stelle / in demselben Bucket aufnehmen.
Eine Kollision benötigt bei der Suche eine spezielle Behandlung durch das Verfahren: Zunächst wird aus einem Suchschlüssel wieder ein Hashwert berechnet, der den Bucket des gesuchten Datenobjektes bestimmt; dann muss noch durch direkten Vergleich des Suchschlüssels mit den Objekten im Bucket das gesuchte Ziel bestimmt werden.
Zur Behandlung von Kollisionen werden kollidierte Daten nach einer Ausweichstrategie in alternativen Feldern oder in einer Liste gespeichert. Schlimmstenfalls können Kollisionen zu einer Entartung der Hashtabelle führen, wenn wenige Hashwerte sehr vielen Objekten zugewiesen wurden, während andere Hashwerte unbenutzt bleiben.
Kollisionsauflösungsstrategien[Bearbeiten | Quelltext bearbeiten]
Um das Kollisions-Problem zu handhaben, gibt es diverse Kollisionsauflösungsstrategien.
Geschlossenes Hashing mit offener Adressierung[Bearbeiten | Quelltext bearbeiten]
Eine Möglichkeit wird geschlossenes Hashing mit offener Adressierung genannt. Wenn dabei ein Eintrag an einer schon belegten Stelle in der Tabelle abgelegt werden soll, wird stattdessen eine andere freie Stelle genommen. Häufig werden drei Varianten unterschieden (vgl. #Algorithmen):
- lineares Sondieren
- es wird um ein konstantes Intervall verschoben nach einer freien Stelle gesucht. Meistens wird die Intervallgröße auf 1 festgelegt.
- quadratisches Sondieren
- Nach jedem erfolglosen Suchschritt wird das Intervall quadriert.
- doppeltes Hashen
- eine weitere Hash-Funktion liefert das Intervall.
Offenes Hashing mit geschlossener Adressierung[Bearbeiten | Quelltext bearbeiten]
Eine weitere Möglichkeit ist offenes Hashing mit geschlossener Adressierung. Anstelle der gesuchten Daten enthält die Hashtabelle hier Behälter (englisch Buckets), die alle Daten mit gleichem Hash-Wert aufnehmen. Bei einer Suche wird also zunächst der richtige Zielbehälter berechnet. Damit wird die Menge der möglichen Ziele erheblich eingeschränkt.
Dennoch müssen abschließend die verbliebenen Elemente im Behälter durchsucht werden. Im schlimmsten Fall kann es passieren, dass alle Elemente gleiche Hash-Werte haben und damit im selben Bucket abgelegt werden. In der Praxis kann das aber durch die Wahl einer geeigneten Größe für die Hashtabelle sowie einer geeigneten Hash-Funktion vermieden werden.
Oft wird die Verkettung durch eine lineare Liste pro Behälter realisiert.
Vorteile[Bearbeiten | Quelltext bearbeiten]
Je nach Anwendungsfall hat eine Hashtabelle Vorteile sowohl in der Zugriffszeit (gegenüber anderen Baumindexstrukturen) als auch im benötigten Speicherplatz (gegenüber gewöhnlichen Arrays).
Idealerweise sollte die Hashfunktion für die zu speichernden Daten so gewählt sein, dass die Anzahl der Kollisionen minimiert wird und unter einer Konstante bleibt; je nach Hashfunktion muss die Hashtabelle dafür ungenutzte Felder enthalten (in der Praxis üblicherweise 20 bis 30 Prozent). Trifft dies zu, dann benötigt eine Hashtabelle mit gespeicherten Elementen per Zugriff (englisch Look-Up) auf einen Hashtabellen-Eintrag im Mittel nur konstanten Zeitaufwand (O(1)).
Im Vergleich dazu ist der Zugriff auf ein Element in einem B-Baum in der Größenordnung von , wobei das n der Anzahl der in der Hashtabelle gespeicherten Einträge entspricht. Die komplette Baum-Datenstruktur benötigt Speicher in der Größenordnung von .
Nachteile[Bearbeiten | Quelltext bearbeiten]
Wegen der möglichen Kollisionen hat eine Hashtabelle im Worst-Case ein sehr schlechtes Zugriffszeit-Verhalten. Dieser wird mit abgeschätzt; es werden dabei also alle Einträge in der Tabelle durchsucht.
Als Füllgrad wird die Anzahl der gespeicherten Elemente geteilt durch die Anzahl aller Buckets bezeichnet:
- Füllgrad = gespeicherte Elemente/Buckets.
Mit steigendem Füllgrad wächst die Wahrscheinlichkeit einer Kollision, und die Entartung nimmt zu. Dann kann nur eine Vergrößerung der Tabelle mit nachfolgender Restrukturierung wieder zu akzeptablem Laufzeitverhalten führen.
Außerdem bringt eine der Suchoperation nachfolgende Nachbarschaftssuche nichts, da eine Ordnungsbeziehung zwischen den Schlüsseln erklärtermaßen nicht gepflegt wird (s. a. Abschnitt Datenbanken).
Varianten[Bearbeiten | Quelltext bearbeiten]
Es gibt mehrere Varianten des Hashverfahrens, die sich für bestimmte Daten besser eignen. Ein wichtiger Faktor hierbei ist die Dynamik, mit der sich die Anzahl der Elemente ändert. Das offene Hashing löst dieses Problem, nimmt aber Einbußen bei den Zugriffszeiten in Kauf. Das geschlossene Hashing ist hingegen auf explizite Strategien zur Kollisionsbehandlung angewiesen.
Vorsicht: Die Bezeichnungen offenes bzw. geschlossenes Hashing werden auch in genau umgekehrter Bedeutung verwendet.
Hashing mit Verkettung[Bearbeiten | Quelltext bearbeiten]
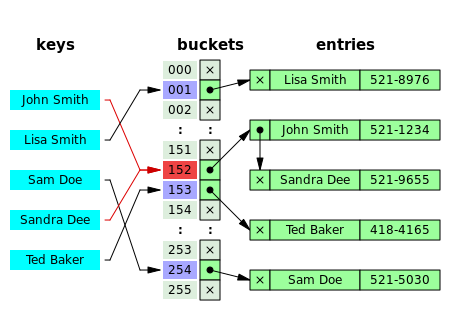
Beim Hashing mit Verkettung (englisch separate chaining) ist die Hash-Tabelle so strukturiert, dass jeder Behälter eine dynamische Datenstruktur aufnehmen kann – beispielsweise eine Liste oder einen Baum. Jeder Schlüssel wird dann in dieser Datenstruktur eingetragen oder gesucht. So ist es problemlos möglich, mehrere Schlüssel in einem Behälter abzulegen, was allerdings zu mehr oder weniger verlängerten Zugriffszeiten führt. Die Effizienz des Zugriffs wird dabei davon bestimmt, wie schnell Datensätze in die gewählte Datenstruktur eingefügt und darin wiedergefunden werden können. Hashing mit Verkettung ist bei Datenbanken eine sehr gängige Indizierungsvariante, wobei sehr große Datenmengen mittels Hashtabellen indiziert werden. Die Größe der Buckets ist in Datenbanksystemen ein Vielfaches der Sektorengröße des Speichermediums. Der Grund dafür ist, dass die Datenmenge nicht mehr im Hauptspeicher gehalten werden kann. Bei einer Suchanfrage muss das Datenbanksystem die Buckets sektorenweise einlesen.
Jeder Behälter ist unabhängig und weist eine Art Liste von Einträgen mit demselben Index auf. Die Zeit für Operationen der Hashtabelle ist die Zeit zum Suchen des Behälters, die konstant ist, plus die Zeit für die Listenoperation. In einer guten Hashtabelle hat jeder Behälter keinen oder einen Eintrag und manchmal zwei oder drei, aber selten mehr. Daher werden für diese Fälle zeit- und raumeffiziente Strukturen bevorzugt. Strukturen, die für eine ziemlich große Anzahl von Einträgen pro Behälter effizient sind, sind nicht erforderlich oder wünschenswert. Wenn diese Fälle häufig auftreten, funktioniert das Hashing nicht gut, und dies muss behoben werden.
Hashing mit offener Adressierung[Bearbeiten | Quelltext bearbeiten]

Dieses Verfahren wird abgekürzt auch offenes Hashing oder geschlossenes Hashing genannt. Der Name offenes Hashing bezieht sich auf die offene Adressierung, während der Name geschlossenes Hashing sich auf die begrenzte Anzahl möglicher Schlüssel im Behälter bezieht.
Beim Hashing mit offener Adressierung kann jedem Behälter nur eine feste Anzahl von Schlüsseln zugewiesen werden. Häufig wählt man einfach einen einzigen möglichen Schlüssel pro Behälter. Im Kollisionsfall muss dann nach einem alternativen Behälter gesucht werden. Dabei geht man so vor, dass man für m Behälter eine ganze Folge von m Hash-Funktionen definiert. Führt die Anwendung der ersten Hash-Funktion, nennen wir sie h1, zu einer Kollision, so wendet man h2 an. Führt diese ebenfalls zu einer Kollision (d. h. der entsprechende Behälter ist bereits belegt), so wendet man h3 an, und so weiter, bis hm bzw. bis ein leerer Behälter gefunden wird. Die Bezeichnung „offene Adressierung“ ergibt sich aus der Eigenschaft, dass durch Kollisionen gleiche Schlüssel unterschiedliche Adressen zugewiesen bekommen können.
Alle Eintragsdatensätze werden im Behälter selbst gespeichert. Wenn ein neuer Eintrag eingefügt werden muss, werden die Behälter untersucht, beginnend mit dem Hash-zu-Slot und fortschreitend in einer bestimmten Prüfsequenz, bis ein unbesetzter Behälter gefunden wird. Bei der Suche nach einem Eintrag werden die Behälter in der gleichen Reihenfolge durchsucht, bis entweder der Zieldatensatz oder ein ungenutzter Behälter gefunden wird, was anzeigt, dass es keinen solchen Schlüssel in der Tabelle gibt. Der Name offenes Hashing bezieht sich darauf, dass der Ort des Elements nicht durch seinen Hashwert bestimmt wird.
Kuckucks-Hashing[Bearbeiten | Quelltext bearbeiten]
Kuckucks-Hashing ist ein weiteres Verfahren, Kollisionen in einer Tabelle zu vermeiden. Der Name leitet sich vom Verhalten des Kuckucks ab, Eier aus einem Nest zu entfernen, um ein eigenes Ei hineinzulegen.
Das Prinzip ist, zwei Hash-Funktionen einzusetzen. Das ergibt zwei mögliche Speicherorte in einer Hashtabelle, was immer eine konstante Zugriffszeit garantiert. Ein neuer Schlüssel wird an einem der zwei möglichen Orte gespeichert. Sollte die erste Zielposition besetzt sein, wird der bereits vorhandene Schlüssel auf seine alternative Position versetzt und an seiner Stelle der neue Schlüssel gespeichert. Sollte die alternative Position besetzt sein, so wird wiederum der Schlüssel auf dieser Position auf seine alternative Position transferiert, und so fort. Wenn diese Prozedur zu einer unendlichen Schleife führt (üblicherweise bricht man nach Schritten ab), wird die Hashtabelle mit zwei neuen Hash-Funktionen neu aufgebaut. Die Wahrscheinlichkeit für ein solches Rehashing liegt in der Größenordnung von für jedes Einfügen.
Algorithmen[Bearbeiten | Quelltext bearbeiten]
Lineares Sondieren[Bearbeiten | Quelltext bearbeiten]
Die einfachste Möglichkeit zur Definition einer solchen Folge besteht darin, so lange den jeweils nächsten Behälter zu prüfen, bis man auf einen leeren Behälter trifft. Die Definition der Folge von Hashfunktionen sieht dann so aus:
Die Anwendung des Operators Modulo hat mit der begrenzten Zahl von Behältern zu tun: Wurde der letzte Behälter geprüft, so beginnt man wieder beim ersten Behälter. Das Problem dieser Methode ist, dass sich so schnell Ketten oder Cluster bilden und die Zugriffszeiten im Bereich solcher Ketten schnell ansteigen. Das lineare Sondieren ist daher wenig effizient. Sein Vorteil ist jedoch, dass – im Gegensatz zu anderen Sondierungsverfahren – alle Behälter der Tabelle benutzt werden.
Um ein Element zu finden, berechnet man und beginnt dort mit der Suche. Man durchläuft das Array, bis entweder das Element gefunden oder eine leerer Behälter erkannt wird. Löschungen sind etwas schwieriger als beim Hashing mit Verkettung, denn man kann nicht einfach eine Suche durchführen und das Element dort löschen, wo man es findet. Löschungen werden häufig mithilfe von sogenannten Tombstones umgesetzt. Beim Löschen eines Elements wird markiert, dass der Behälter leer ist und zuvor belegt war. Beim Suchen bleibt man nicht bei einem Tombstone stehen. Stattdessen setzt man die Suche fort. Man muss dabei auf das Ende des Arrays achten und gegebenenfalls wieder am Anfang beginnen. Beim Einfügen kann jeder Tombstone, auf den man stößt durch einen leeren Behälter ersetzt werden.
In der Praxis ist lineares Sondieren eine der schnellsten Hashing-Algorithmen. Vorteilhaft ist der geringe Speicheraufwand. Man benötigt lediglich ein Array und eine sehr einfache Hashfunktion. Hervorragende Lokalität: Bei Kollisionen suchen wir nur an benachbarten Orten im Array. Bei der linearen Abtastung kommt es zu erheblichen Leistungseinbußen, wenn der Lastfaktor hoch wird. Die Anzahl der Kollisionen nimmt tendenziell mit der Anzahl der bestehenden Kollisionen zu. Dies wird als primäres Clustering bezeichnet.[1]
Wenn Elemente in eine Array mit Behältern eingefügt werden, ist der Lastfaktor . Der Erwartungswert für die Anzahl der Schlüssel pro Behälter bei einer nicht erfolgreichen Suche beträgt dann . Der Erwartungswert bei einer erfolgreichen Suche eines zufälligen Elements beträgt .[2][3]
Quadratisches Sondieren[Bearbeiten | Quelltext bearbeiten]
Wie beim linearen Sondieren wird nach einem neuen freien Speicher gesucht, allerdings nicht sequenziell, sondern mit stetig quadratisch wachsendem Abstand zur ursprünglichen Position und in beide Richtungen. Verursacht eine Kollision, so werden nacheinander usw. probiert. In Formeln ausgedrückt:
Den ständigen Wechsel des Vorzeichens bei dieser Kollisionsstrategie nennt man auch „alternierendes quadratisches Sondieren“ oder „quadratisches Sondieren mit Verfeinerung“. Wählt man die Anzahl der Behälter geschickt (nämlich , ist Primzahl), so erzeugt jede Sondierungsfolge bis eine Permutation der Zahlen 0 bis ; so wird also sichergestellt, dass jeder Behälter getroffen wird.[4]
Quadratisches Sondieren ergibt keine Verbesserung für die Wahrscheinlichkeit eine Sondierung durchführen zu müssen (), kann aber die Wahrscheinlichkeit von Kollisionen während der Sondierung () herabsetzen, d. h. Clusterbildung wird vermieden.
Das quadratische Sondieren verhindert die Cluster, die beim linearen Sondieren entstehen, ist aber nicht optimal. Beim quadratische Sondieren entsteht sogenanntes sekundäres Clustering. Dies geschieht, denn wenn zwei Schlüssel nahe beieinander liegende Hashwerte haben, liegen die entsprechenden sondierten Behälter ebenfalls nahe beieinander. Zusätzlich gibt es einen anderen Nachteil. Im Gegensatz zum linearen Sondieren, das garantiert jeden Behälter ausprobiert, stehen für das quadratische Sondieren in einigen Fällen nur Behälter zur Auswahl.[5]
Der Erwartungswert für die Anzahl der Schlüssel pro Behälter bei einer nicht erfolgreichen Suche beträgt . Der Erwartungswert bei einer erfolgreichen Suche eines zufälligen Elements beträgt .[3]
Doppel-Hashing[Bearbeiten | Quelltext bearbeiten]
Beim Doppel-Hashing werden zwei unabhängige Hash-Funktionen und angewandt. Diese heißen unabhängig, wenn die Wahrscheinlichkeit für eine sogenannte Doppelkollision, d. h. gleich und damit minimal ist. Die Folge von Hash-Funktionen, die nun mittels und gebildet werden, sieht so aus:
Die Kosten für diese Methode sind nahe den Kosten für ein ideales Hashing.
Eine interessante Variante des Doppel-Hashing ist das Robin-Hood-Hashing. Die Idee ist, dass ein neuer Schlüssel einen bereits eingefügten Schlüssel verdrängen kann, wenn seine Prüfwert größer ist als die des Schlüssels an der aktuellen Position. Der Nettoeffekt davon ist, dass es die Worst Case Suchzeiten in der Tabelle reduziert. Weil sowohl der Worst Case als auch die Variation der Anzahl der Sonden drastisch reduziert werden, besteht eine interessante Variation darin, die Tabelle beginnend mit der erwarteten erfolgreichen Prüfwert zu durchsuchen und dann von dieser Position aus in beide Richtungen zu erweitern.
Der Erwartungswert für die Anzahl der Schlüssel pro Behälter bei einer nicht erfolgreichen Suche beträgt . Der Erwartungswert bei einer erfolgreichen Suche eines zufälligen Elements beträgt .[3]
Brent-Hashing[Bearbeiten | Quelltext bearbeiten]
Beim Brent-Hashing wird geprüft, ob der Platz, an dem das Element eingefügt werden soll, frei ist. Ist das der Fall, dann wird das Element dort eingefügt. Ist der Platz jedoch belegt, dann wird anhand des gerade berechneten Platzes jeweils für das einzufügende Element und für das Element, das schon an dem Platz ist, ein neuer Platz in der Tabelle berechnet. Sind die beiden neu berechneten Plätze auch belegt, wiederholt sich die Prozedur für den neu berechneten belegten Platz des einzufügenden Elementes. Wird jedoch für das einzufügende Element ein Platz berechnet, der frei ist, wird das Element dort eingefügt. Ist der Platz jedoch belegt und der berechnete Platz frei für das Element, das im vorherigen Durchlauf den Platz für das einzufügende Element belegt hat, dann werden die beiden Plätze der Elemente vertauscht und damit konnte das einzufügende Element in der Tabelle untergebracht werden.
Dynamisches Hashing[Bearbeiten | Quelltext bearbeiten]
Bei steigendem Füllgrad der Tabelle steigt die Wahrscheinlichkeit von Kollisionen deutlich an. Spätestens wenn die Anzahl der indizierten Datensätze größer ist, als die Kapazität der Tabelle, werden Kollisionen unvermeidbar. Das bedeutet, dass das Verfahren einen zunehmenden Aufwand zur Kollisionslösung aufwenden muss. Um dies zu vermeiden, wird beim Dynamischen Hashing die Hashtabelle bei Bedarf vergrößert. Dies hat jedoch zwangsläufig Auswirkungen auf den Wertebereich der Hash-Funktion, der nun ebenfalls erweitert werden muss. Eine Änderung der Hash-Funktion wiederum hat jedoch den nachteiligen Effekt, dass sich ebenfalls die Hash-Werte für bereits gespeicherte Daten ändern. Für das dynamische Hashing wurde dafür eigens eine Klasse von Hash-Funktionen entwickelt, deren Wertebereich vergrößert werden kann, ohne die bereits gespeicherten Hash-Werte zu verändern.
Vorteile[Bearbeiten | Quelltext bearbeiten]
- Es gibt keine obere Grenze für das Datenvolumen
- Einträge können ohne Probleme gelöscht werden
- Adresskollisionen führen nicht zur Clusterbildung.
Nachteile[Bearbeiten | Quelltext bearbeiten]
Falls nicht eine ordnungserhaltende Hashfunktion zum Einsatz kam:
- kein effizientes Durchlaufen der Einträge nach einer Ordnung
- keine effiziente Suche nach dem Eintrag mit dem kleinsten oder größten Schlüssel
Anwendung[Bearbeiten | Quelltext bearbeiten]
Hashtabellen werden in praktisch jeder modernen Applikation eingesetzt, etwa zur Implementierung von Mengen (Sets) oder Caches.
Assoziative Arrays[Bearbeiten | Quelltext bearbeiten]
Ein typischer Anwendungsfall sind daneben assoziative Arrays (auch bekannt als Map, Lookup Table, Dictionary oder Wörterbuch); das Nachschlagen der mit einem Schlüssel assoziierten Daten kann mittels einer Hashtabelle schnell und elegant implementiert werden.
Symboltabellen[Bearbeiten | Quelltext bearbeiten]
Symboltabellen, wie sie Compiler oder Interpreter verwenden, werden meist ebenfalls als Hashtabelle realisiert.
Datenbanken[Bearbeiten | Quelltext bearbeiten]
Wichtig sind Hashtabellen auch für Datenbanken zur Indizierung von Tabellen. Ein Hashindex kann unter günstigen Bedingungen zu idealen Zugriffszeiten führen.
Hashtabellen ermöglichen eine sehr schnelle Suche in großen Datenmengen, da mit der Berechnung des Hashwertes in einem einzigen Schritt die Anzahl der möglichen Zielobjekte eingeschränkt wird. Damit gehören Hashtabellen zu den effizientesten Indexstrukturen.
Ein großer Nachteil ist jedoch die Gefahr der Entartung durch Kollisionen, die bei einem stetigen Wachstum der Datenmenge unausweichlich sind (wenn die Tabelle nicht vergrößert und jedes darin enthaltene Element neu gehasht wird). Daher, wegen ungünstiger IO-Zugriffsmuster, wenn die Hashtabelle auf einem Datenträger gespeichert ist und der fehlenden Möglichkeit Intervalle gemäß einer Ordnungsrelation effizient zu iterieren, muss der Einsatz von Datenbanksystemen gegenüber alternativen Indexdatenstrukturen, wie z. B. B+-Bäumen, abgewogen werden.
Die meisten Hashfunktionen erlauben nicht die Bewegung zum nächsten oder vorherigen Datensatz gemäß einer Ordnungsrelation, da sie gezielt die Daten „mischen“, um sie gleichmäßig im Werteraum zu verteilen. Nur spezielle „ordnungserhaltende“ Hashfunktionen erlauben eine derartige Iteration gemäß ihrer Ordnungsrelation und damit die Abfrage mit Ungleichheitsverknüpfungen („größer als“, „kleiner als“) oder den sortierten Zugriff auf alle Werte.[6] Um solche Verfahren effizient einsetzen zu können, ist meist eine vorherige Analyse der Datenverteilung notwendig. Sie werden daher meist nur in Datenbanksystemen angewendet, die eine solche Analyse auch beispielsweise zur Anfrageoptimierung durchführen.
Siehe auch[Bearbeiten | Quelltext bearbeiten]
- Bloomfilter
- R-Baum, effektives Indexverfahren für mehrdimensionale Daten
- Verteilte Hashtabelle
- Nebenläufige Hashtabelle
Literatur[Bearbeiten | Quelltext bearbeiten]
- MAURER, Ward Douglas: Hash Table Methods. In: ACM Computing Surveys (CSUR). Band 7, Nr. 1, März 1975, S. 5–19, doi:10.1145/356643.356645 (englisch).
- LITWIN, Witold: Linear Hashing: a new tool for file and table addressing. In: IEEE Int. Conf. Very Large Database VLDB'80. Band 6, Oktober 1980, S. 212–223 (englisch, northwestern.edu [PDF; abgerufen am 18. März 2021]).
- CELIS, Pedro; LARSON, Per-Ake; MUNRO, J. Ian: Robin hood hashing. In: 26th Annual Symposium on Foundations of Computer Science (SFCS'1985). 1985, S. 281–288, doi:10.1109/SFCS.1985.48 (englisch).
- PAGH, Rasmus; RODLER, Flemming Friche: Cuckoo hashing. In: Journal of Algorithms. Band 51, Nr. 2, 2004, S. 122–144, doi:10.1016/j.jalgor.2003.12.002 (englisch).
- BURKHARD, Walter A.: Double hashing with passbits. In: Information processing letters. Band 96, Nr. 5, 16. Dezember 2005, S. 162–166, doi:10.1016/j.ipl.2005.08.005 (englisch).
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest: Introduction to Algorithms. 1184 Seiten; The MIT Press 2001, ISBN 0-262-53196-8.
- Alfons Kemper, André Eickler: Datenbanksysteme – Eine Einführung. 7. Auflage, Oldenbourg Verlag 2009, ISBN 3-486-57690-9. Seite 220f
- Christian Ullenboom: Java ist auch eine Insel, 1444 Seiten; Galileo Press 2007, ISBN 3-89842-838-9; online als Openbook verfügbar.
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Umfangreiche Hashbibliothek mit weitreichender Analysefunktionalität
- Cuckoo Hashing (englisch, PDF, 169 KiB)
- Hash Table
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Stanford University: Linear Probing
- ↑ Uri Zwick, Tel Aviv University: Hash Tables: Linear Probing
- ↑ a b c O. Bittel, Hochschule Konstanz: Algorithmen und Datenstrukturen – Hashverfahren
- ↑ Martin Lercher, Heinrich-Heine-Universität Düsseldorf: Algorithmen und Datenstrukturen - Hash-Verfahren
- ↑ Dave Mount, University of Maryland: Hashing
- ↑ Davi de Castro Reis, Djamel Belazzougui, Fabiano Cupertino Botelho: Minimal Perfect Hash Functions - Introduction. SourceForge, abgerufen am 8. November 2010 (englisch).






























