Tiefensuche

Tiefensuche (englisch depth-first search, DFS) ist in der Informatik ein Verfahren zum Suchen von Knoten in einem Graphen. Sie zählt zu den uninformierten Suchalgorithmen. Im Gegensatz zur Breitensuche wird bei der Tiefensuche zunächst ein Pfad vollständig in die Tiefe beschritten, bevor abzweigende Pfade beschritten werden[1]. Dabei sollen alle erreichbaren Knoten des Graphen besucht werden. Für Graphen mit potenziell wenigen, langen Pfaden bietet sich die beschränkte Tiefensuche an, bei der jeder Pfad nur bis zu einer bestimmten Tiefe beschritten wird.
Eine Verbesserung der Tiefensuche ist die iterative Tiefensuche.
Arbeitsweise[Bearbeiten | Quelltext bearbeiten]
Die Tiefensuche ist ein uninformierter Suchalgorithmus, welche durch Expansion des jeweils ersten auftretenden Nachfolgeknotens im Graphen nach und nach vom Startknoten aus weiter in die Tiefe sucht. In welcher Reihenfolge die Nachfolger eines Knotens dabei bestimmt werden, hängt von der Repräsentation der Nachfolger ab. Bei der Repräsentation über eine Adjazenzliste mittels einer verketteten Liste werden beispielsweise die Knoten in der Reihenfolge ihres Eintrags in dieser Liste durchlaufen. Im oben angegebenen Bild wird implizit davon ausgegangen, dass die Nachfolger von links nach rechts ausgewählt werden.
Für ungerichtete Graphen sieht das Verfahren wie folgt aus: Zuerst wird ein Startknoten ausgewählt. Von diesem Knoten aus wird nun die erste Kante betrachtet und getestet, ob der gegenüberliegende Knoten schon entdeckt wurde bzw. das gesuchte Element ist. Ist dies noch nicht der Fall, so wird rekursiv für diesen Knoten die Tiefensuche aufgerufen, wodurch wieder der erste Nachfolger dieses Knotens expandiert wird. Diese Art der Suche wird solange fortgesetzt, bis das gesuchte Element entweder gefunden wurde oder die Suche bei einer Senke im Graphen angekommen ist und somit keine weiteren Nachfolgeknoten mehr untersuchen kann. An dieser Stelle kehrt der Algorithmus nun zum zuletzt expandierten Knoten zurück und untersucht den nächsten Nachfolger des Knotens. Sollte es hier keine weiteren Nachfolger mehr geben, geht der Algorithmus wieder Schritt für Schritt zum jeweiligen Vorgänger zurück und versucht es dort erneut. Ein Beispiel für die Anwendung der Tiefensuche auf einen Baum zeigt die Animation.
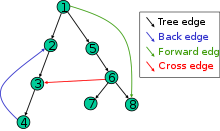
Die Kanten des Graphen, die vom Algorithmus zum Durchlaufen des Graphen benutzt werden, werden als Baumkanten bezeichnet. Diejenigen Kanten, die nicht benutzt werden und von einem Knoten zu einem anderen Knoten im selben Teilbaum führen, der bei der Tiefensuche später besucht wird, heißen Vorwärtskanten. Diejenigen Kanten, die nicht benutzt werden und von einem Knoten zu einem anderen Knoten im selben Teilbaum führen, der bei der Tiefensuche bereits vorher besucht wurde, heißen Rückwärtskanten. Diejenigen Kanten, die „quer“ von einem Teilbaum zu einem anderen Teilbaum verlaufen, heißen Querkanten. Innerhalb des Tiefensuchbaums würde der Pfad zwischen zwei über eine Querkante verbundenen Knoten zunächst ein Auf- und dann ein Absteigen im Baum erfordern. Vorwärtskanten, Rückwärtskanten, Querkanten und Baumkanten ergeben insgesamt die Kantenmenge des Graphen.
 |
 |
Der Index der Rekursionstiefe der rekursiven Methode oder Prozedur für die Tiefensuche entspricht dem Knotenabstand des aktuell durchlaufenen Knotens vom Startknoten im in der rechten Abbildung gezeigten Baum. Dieser Index müsste, um zum Beispiel auf der Konsole ausgegeben zu werden, in einer Variablen gespeichert werden. Diese rekursive Methode oder Prozedur wird so oft aufgerufen, wie die Anzahl der Knoten des Graphen ist. Die Rekursion bricht ab, wenn der aktuell durchlaufene Knoten nur Nachbarknoten hat, die schon vorher durchlaufen wurden.
Im Beispiel mit den Städten (siehe oben) gibt es folgende rekursive Aufrufe:
- Hannover (Startknoten, Rekursionstiefe 0)
- Frankfurt (Nachbarknoten von Hannover, Rekursionstiefe 1)
- Zürich (Nachbarknoten von Frankfurt, Rekursionstiefe 2)
- München (Nachbarknoten von Zürich, Rekursionstiefe 3)
- Stuttgart (Nachbarknoten von München, Rekursionstiefe 4)
- Hamburg (Nachbarknoten von Stuttgart, Rekursionstiefe 5)
- Mannheim (Nachbarknoten von Hamburg, Rekursionstiefe 6)
- Dresden (Nachbarknoten von Stuttgart, Rekursionstiefe 5)
- Wien (Nachbarknoten von München, Rekursionstiefe 4)
- Berlin (Nachbarknoten von Wien, Rekursionstiefe 5)
Der Knotenabstand bezieht sich immer auf den Startknoten. Im links dargestellten ungerichteten Graphen ist es Hannover. Bei gerichteten Graphen ist der Knotenabstand zwischen zwei verschiedenen Knoten nicht unbedingt symmetrisch.
Der Baum, den die Tiefensuche durchläuft, ist ein Spannbaum des Graphen und hängt vom Startknoten ab. Es ist außerdem wichtig, ob es sich um einen gerichteten Graphen oder ungerichteten Graphen handelt.
Der Knotenabstand und die Rekursionstiefe ist nur für zusammenhängende Graphen definiert und hängt vom Startknoten ab. Für nicht zusammenhängende Graphen ist der Knotenabstand und die Rekursionstiefe nur innerhalb jeder Zusammenhangskomponente definiert.
Hinweis: Der in der Abbildung links oben mit den Städten gezeigte Graph ist ein ungerichteter Graph. Die Reihenfolge der durchlaufenen Knoten kann sich ändern, wenn stattdessen ein anderer Startknoten oder ein gerichteter Graph genommen wird, der nicht symmetrisch ist.
Algorithmen[Bearbeiten | Quelltext bearbeiten]
- Bestimme den Knoten, an dem die Suche beginnen soll
- Expandiere den Knoten und speichere der Reihenfolge nach den kleinsten/größten (optional) noch nicht erschlossenen Nachfolger in einem Stack
- Rufe rekursiv für jeden der Knoten in dem Stack DFS auf
- Falls das gesuchte Element gefunden wurde, brich die Suche ab und liefere ein Ergebnis
- Falls es keine nicht erschlossenen Nachfolger mehr gibt, lösche den obersten Knoten aus dem Stack und rufe für den jetzt oberen Knoten im Stack DFS auf
DFS(node, goal)
{
if (node == goal)
{
return node;
}
else
{
stack := expand (node)
while (stack is not empty)
{
node' := pop(stack);
DFS(node', goal);
}
}
}
Erzeugen des Tiefensuchwaldes[Bearbeiten | Quelltext bearbeiten]
Der folgende rekursive Algorithmus in Pseudocode erzeugt den Tiefensuchwald eines Graphen G mittels Setzen von Discovery- und Finishing-Times und Färben der Knoten. In Anlehnung an Cormen et al. werden zunächst alle Knoten weiß gefärbt. Anschließend startet die Tiefensuche per Definition beim alphabetisch kleinsten Knoten und färbt diesen grau. Danach wird, wie oben beschrieben rekursiv dessen weißer Nachbar betrachtet und grau gefärbt. Existiert kein weißer Nachbar mehr, kommt es zum Backtracking, während dessen alle durchwanderten Knoten schwarz gefärbt werden.[2]
DFS(G)
for each v of G // Alle Knoten weiß färben, Vorgänger auf nil setzen
{
col[v] = 'w';
pi[v] = nil;
}
time = 0;
for each u of G // Für alle weißen Knoten: DFS-visit aufrufen
{
if col[u] == 'w'
DFS-visit(u);
}
DFS-visit(u)
1 col[u] = 'g'; // Aktuellen Knoten grau färben
2 time++; // Zeitzähler erhöhen
3 d[u] = time; // Entdeckzeit des aktuellen Knotens setzen
4 for each v of Adj[u] // Für alle weißen Nachbarn des aktuellen Knotens
5 {
6 if col[v] == 'w'
7 {
8 pi[v] = u; // Vorgänger auf aktuellen Knoten setzen
9 DFS-visit(v); // DFS-visit aufrufen
10 }
11 if col[v] == 'g'
12 {
13 // Zyklus entdeckt
14 }
15 }
16 col[u] = 's'; // Aktuellen Knoten schwarz färben
17 time++;
18 f[u] = time; // Finishing-Time des aktuellen Knotens setzen
Den Zeitstempel (siehe Zeilen 2, 17, 18) kann man weiterhin für eine topologische Sortierung verwenden. Nachdem ein Knoten schwarz gefärbt wurde, wird er einer Liste, absteigend nach den Werten f[u] für die Zeitstempel, hinzugefügt und man erhält eine topologische Reihenfolge. Wird ein Zyklus (siehe Zeile 9) entdeckt, ist dies nicht mehr möglich.
Programmierung[Bearbeiten | Quelltext bearbeiten]
Das folgende Beispiel in der Programmiersprache C# zeigt die Implementierung der Tiefensuche für einen gerichteten Graphen. Der gerichtete Graph wird als Klasse DirectedGraph deklariert. Die Methode DepthFirstSearch, die die Knoten durchläuft und in einer Liste speichert, verwendet einfache Rekursion. Bei der Ausführung des Programms wird die Methode Main verwendet, die die Liste der markierten Knoten auf der Konsole ausgibt.[3]
using System;
using System.Collections.Generic;
// Deklariert die Klasse für die Knoten des Graphen
class Node
{
public int index;
public string value;
public List<Node> adjacentNodes = new List<Node>(); // Liste der Nachbarknoten
}
// Deklariert die Klasse für den gerichteten Graphen
class DirectedGraph
{
// Diese Methode verbindet die Knoten startNode und targetNode miteinander.
public void ConnectNodes(Node startNode, Node targetNode)
{
startNode.adjacentNodes.Add(targetNode);
}
}
class Program
{
// Diese Methode gibt die Liste der Knoten in der Form A, B, C, ... als Text zurück.
public static string ToString(List<Node> traversedNodes)
{
string text = "";
for (int i = 0; i < traversedNodes.Count; i++) // for-Schleife, die die Knoten durchläuft
{
text += traversedNodes[i].value + ", ";
}
text = text.Substring(0, text.Length - 2);
return text;
}
// Diese Methode durchläuft die Knoten des gerichteten Graphen mit einer Tiefensuche
public static void DepthFirstSearch(Node startNode, List<Node> traversedNodes)
{
traversedNodes.Add(startNode); // Fügt den aktuellen Knoten der Menge der markierten Knoten hinzu
foreach (Node node in startNode.adjacentNodes) // foreach-Schleife, die alle benachbarten Knoten des Knotens durchläuft
{
if (!traversedNodes.Contains(node)) // Wenn der Knoten noch nicht markiert wurde
{
DepthFirstSearch(node, traversedNodes); // Rekursiver Aufruf der Methode mit dem Nachbarknoten als Startknoten
}
}
}
// Hauptmethode, die das Programm ausführt
public static void Main(String[] args)
{
// Deklariert und initialisiert 4 Knoten
Node node1 = new Node{index = 0, value = "A"};
Node node2 = new Node{index = 1, value = "B"};
Node node3 = new Node{index = 2, value = "C"};
Node node4 = new Node{index = 3, value = "D"};
// Erzeugt einen gerichteten Graphen
DirectedGraph directedGraph = new DirectedGraph();
// Verbindet Knoten des Graphen miteinander
directedGraph.ConnectNodes(node1, node2);
directedGraph.ConnectNodes(node1, node3);
directedGraph.ConnectNodes(node2, node3);
directedGraph.ConnectNodes(node3, node1);
directedGraph.ConnectNodes(node3, node4);
directedGraph.ConnectNodes(node4, node4);
List<Node> traversedNodes = new List<Node>(); // Liste der Knoten für die Tiefensuche
DepthFirstSearch(node3, traversedNodes); // Aufruf der Methode
Console.WriteLine(ToString(traversedNodes)); // Ausgabe auf der Konsole
Console.ReadLine();
}
}
Hinweise: Für die Nachbarknoten wurde eine Liste als Datentyp verwendet, damit die Reihenfolge der durchlaufenen Knoten eindeutig ist und die Knoten in allen Ebenen von links nach rechts durchlaufen werden. Für den Datentyp Menge zum Beispiel muss das nicht der der Fall sein. Statt dem HashSet (Menge) visitedNodes kann auch eine Liste oder ein Array vom Typ bool (Boolesche Variable) verwendet werden, wie im Einzelnachweis gezeigt.[3]
Eigenschaften[Bearbeiten | Quelltext bearbeiten]
Im Folgenden werden Speicherbedarf und Laufzeit des Algorithmus in Landau-Notation angegeben. Wir gehen außerdem von einem gerichteten Graphen aus.
Speicherplatz[Bearbeiten | Quelltext bearbeiten]
Der Speicherbedarf des Algorithmus wird ohne den Speicherplatz für den Graphen, wie er übergeben wird, angegeben, denn dieser kann in verschiedenen Formen mit unterschiedlichem Speicherbedarf vorliegen, z. B. als verkettete Liste, als Adjazenzmatrix oder als Inzidenzmatrix.
Für die oben beschriebene Prozedur DFS(G) werden zunächst alle Knoten weiß gefärbt und die Referenzen für deren Vorgänger entfernt. Diese Informationen benötigt also für jeden Knoten konstanten Speicherplatz, also . Insgesamt ergibt sich ein linearer Speicherbedarf von , abhängig von der Anzahl der Knoten (englisch vertices). Der Speicherbedarf der Variable time ist mit konstantem gegenüber vernachlässigbar. Anschließend wird für jeden Knoten u die Prozedur DFS-visit(u) aufgerufen. Da es sich hierbei nur um Kontrollstrukturen handelt, tragen sie nicht zum Speicherbedarf bei.
Die Prozedur DFS-visit(u) arbeitet auf der bereits aufgebauten Speicherstruktur in der alle Knoten abgelegt sind und erweitert diese pro Knoten noch um die Entdeckzeit und die Finishing-Time, jeweils konstant . Das ändert nichts am bisherigen linearen Speicherbedarf . Da sonst in DFS-visit(u) keine weiteren Variablen mehr eingeführt werden, hat die Tiefensuche einen Speicherbedarf von .
Laufzeit[Bearbeiten | Quelltext bearbeiten]
Falls der Graph als Adjazenzliste gespeichert wurde, müssen im Worst Case alle möglichen Pfade zu allen möglichen Knoten betrachtet werden. Damit beträgt die Laufzeit von Tiefensuche , wobei für die Anzahl der Knoten und für die Anzahl der Kanten im Graph stehen.[4]
Vollständigkeit[Bearbeiten | Quelltext bearbeiten]
Falls ein Graph unendlich groß ist oder kein Test auf Zyklen durchgeführt wird, so ist die Tiefensuche nicht vollständig. Es kann also sein, dass ein Ergebnis – obwohl es existiert – nicht gefunden wird.
Optimalität[Bearbeiten | Quelltext bearbeiten]
Tiefensuche ist insbesondere bei monoton steigenden Pfadkosten nicht optimal, da eventuell ein Ergebnis gefunden wird, zu welchem ein sehr viel längerer Pfad führt als zu einem alternativen Ergebnis. Dafür wird ein solches Ergebnis im Allgemeinen deutlich schneller gefunden als bei der in diesem Fall optimalen, aber sehr viel speicheraufwendigeren Breitensuche. Als Kombination von Tiefen- und Breitensuche gibt es die iterative Tiefensuche.
Anwendungen[Bearbeiten | Quelltext bearbeiten]
Die Tiefensuche ist indirekt an vielen komplexeren Algorithmen für Graphen beteiligt. Beispiele:
- Das Auffinden aller starken Zusammenhangskomponenten eines Graphen.
- Das Ermitteln von 2-zusammenhängenden Komponenten.
- Das Ermitteln von 3-zusammenhängenden Komponenten.
- Das Ermitteln der Brücken eines Graphen.
- Einen Graphen testen, ob er ein planarer Graph ist.[5][6]
- Bei einem Baum, der Abhängigkeiten darstellt, ergeben die sortierten finish-Zeiten (siehe Pseudocode oben) eine invers-topologische Sortierung.
- Mit der Tiefensuche kann man Graphen in Laufzeit auf Kreise testen und im Falle von Kreisen die dazugehörige Kantenfolge ausgeben.[7]
- Ein kreisfreier Graph kann mit der Tiefensuche in Laufzeit topologisch sortiert werden.[7]
- Das Lösen von Rätseln mit nur einer Lösung, z. B. Irrgärten. Die Tiefensuche kann angepasst werden, um alle Lösungen für einen Irrgarten zu finden, indem nur Knoten auf dem aktuellen Pfad in die besuchte Menge aufgenommen werden.
- Für das Erzeugen eines Irrgartens kann eine zufällige Tiefensuche verwendet werden.
Literatur[Bearbeiten | Quelltext bearbeiten]
- Stuart Russell, Peter Norvig: Artificial Intelligence: A Modern Approach. 2. Auflage. Prentice Hall, 2002.
- Sven Oliver Krumke, Hartmut Noltemeier: Graphentheoretische Konzepte und Algorithmen. 3. Auflage. Springer Vieweg, 2012, ISBN 978-3-8348-1849-2
Weblinks[Bearbeiten | Quelltext bearbeiten]
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Volker Turau: Algorithmische Graphentheorie. 3. Auflage. Oldenbourg Wissenschaftsverlag, München 2009, ISBN 978-3-486-59057-9, S. 94–98.
- ↑ Thomas H. Cormen, Charles Leiserson, Ronald L. Rivest, Clifford Stein: Algorithmen – Eine Einführung. 3. Auflage. Oldenbourg Wissenschaftsverlag, München 2010, ISBN 978-3-486-59002-9, S. 613–622.
- ↑ a b GeeksforGeeks: Depth First Search or DFS for a Graph
- ↑ Thomas Ottmann, Peter Widmayer: Algorithmen und Datenstrukturen. 5. Auflage. Spektrum Akademischer Verlag, Heidelberg 2012, ISBN 978-3-8274-2803-5, S. 589–668.
- ↑ John Hopcroft, Robert E. Tarjan: Efficient planarity testing. In: Journal of the Association for Computing Machinery. 21. Jahrgang, Nr. 4, 1974, S. 549–568, doi:10.1145/321850.321852.
- ↑ H. de Fraysseix, P. Ossona de Mendez, P. Rosenstiehl: Trémaux Trees and Planarity. In: International Journal of Foundations of Computer Science. 17. Jahrgang, Nr. 5, 2006, S. 1017–1030, doi:10.1142/S0129054106004248, arxiv:math/0610935.
- ↑ a b Sven Oliver Krumke, Hartmut Noltemeier: Graphentheoretische Konzepte und Algorithmen. 3. Auflage. Springer Vieweg, Wiesbaden 2012, ISBN 978-3-8348-1849-2, S. 152–157.







