Proportionale Fehlerreduktionsmaße
Proportionale Fehlerreduktionsmaße (proportionale Fehlerreduktion (PFR) englisch proportionate reduction of error, kurz: PRE, daher auch PRE-Maße) geben indirekt die Stärke des Zusammenhangs zwischen zwei Variablen und an.
Definition[Bearbeiten | Quelltext bearbeiten]
Proportionale Fehlerreduktionsmaße werden definiert als
- ,
wobei der Fehler bei der Vorhersage der abhängigen Variablen ohne Kenntnis des Zusammenhangs und der Fehler bei der Vorhersage der abhängigen Variablen mit Kenntnis des Zusammenhangs mit ist.
Da gilt (weil man annimmt, dass die Kenntnis des Zusammenhangs korrekt ist; der Vorhersagefehler nimmt also bei Verwendung der Kenntnis ab), folgt . Ein Wert von Eins bedeutet, dass bei Kenntnis der unabhängigen Variable der Wert der abhängigen Variable perfekt vorhergesagt werden kann. Ein Wert von Null bedeutet, dass die Kenntnis der unabhängigen Variablen keine Verbesserung in der Vorhersage der abhängigen Variable ergibt.
Der Vorteil ist, dass damit alle proportionalen Fehlerreduktionsmaße in gleicher Weise unabhängig vom Skalenniveau interpretiert werden können. Als Vergleichsmaßstab kann daher das Bestimmtheitsmaß dienen, da es ein proportionales Fehlerreduktionsmaß ist, oder folgende Daumenregel:[1]
- : Keine Beziehung,
- : Schwache Beziehung,
- : Mittlere Beziehung und
- : Starke Beziehung.
Der Nachteil ist, dass
- die Richtung des Zusammenhangs nicht berücksichtigt werden kann, da Richtungen nur bei ordinalen oder metrischen Variablen angegeben werden können und
- die Größe der Fehlerreduktion davon abhängt, wie die Vorhersage unter Kenntnis des Zusammenhangs gemacht wird. Ein kleiner Wert des proportionalen Fehlerreduktionmaßes bedeutet nicht, dass es keinen Zusammenhang zwischen den Variablen gibt.
Da eine Variable abhängig und die andere unabhängig ist, unterscheidet man zwischen symmetrischen und asymmetrischen proportionalen Fehlerreduktionsmaßen:
| Skalenniveau der | Maß | |||
|---|---|---|---|---|
| unabhängigen Variable X | abhängigen Variable Y | Name | Bemerkung | |
| nominal | nominal | Goodman und Kruskals [2] | Es gibt ein symmetrisches und ein asymmetrisches Maß. | |
| nominal | nominal | Goodman und Kruskals [2] | Es gibt ein symmetrisches und ein asymmetrisches Maß. | |
| nominal | nominal | Unsicherheitskoeffizient oder Theils U[3] | Es gibt ein symmetrisches und ein asymmetrisches Maß. | |
| ordinal | ordinal | Goodman und Kruskals [2] | Es gibt nur ein symmetrisches Maß. | |
| nominal | metrisch | Es gibt nur ein asymmetrisches Maß. | ||
| metrisch | metrisch | Bestimmtheitsmaß | Es gibt nur ein symmetrisches Maß. | |
Bestimmtheitsmaß[Bearbeiten | Quelltext bearbeiten]
Für die Vorhersage unter Unkenntnis des Zusammenhangs zwischen zwei metrischen Variablen und dürfen nur Werte der abhängigen Variablen benutzt werden. Der einfachste Ansatz ist , also die Annahme eines konstanten Wertes. Dieser Wert soll die Optimalitätseigenschaft erfüllen, also die Summe der Abweichungsquadrate minimieren. Daraus folgt, dass das arithmetische Mittel ist, also . Daher ist der Vorhersagefehler unter Unkenntnis des Zusammenhangs
- .
Für die Vorhersage unter Kenntnis des Zusammenhangs nutzen wir die lineare Regression aus:
- .
Das Bestimmtheitsmaß ist dann ein proportionales Fehlerreduktionsmaß, da gilt
Werden die Rollen der abhängigen und unabhängigen Variable vertauscht, so ergibt sich der gleiche Wert für . Daher gibt es nur ein symmetrisches Maß.
Goodman und Kruskals λ und τ[Bearbeiten | Quelltext bearbeiten]
Goodman und Kruskals λ[Bearbeiten | Quelltext bearbeiten]
Die Vorhersage unter Unkenntnis des Zusammenhangs ist die Modalkategorie der abhängigen Variable und der Vorhersagefehler
mit die absolute Häufigkeit in der Modalkategorie und die Anzahl der Beobachtungen.
Die Vorhersage unter Kenntnis des Zusammenhangs ist die Modalkategorie der abhängigen Variable in Abhängigkeit von den Kategorien der unabhängigen Variablen und der Vorhersagefehler ist
mit die absolute Häufigkeit für die jeweilige Kategorie der unabhängigen Variablen und die absolute Häufigkeit der Modalkategorie in Abhängigkeit von den Kategorien der unabhängigen Variablen.
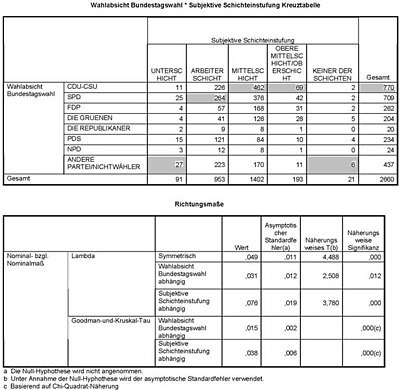
Beispiel
Im Beispiel rechts ergibt sich für die abhängige Variable „Wahlabsicht Bundestagswahl“ bei Unkenntnis des Zusammenhangs als der Vorhersagewert „CDU/CSU“ und damit eine Fehlervorhersage .
Je nach Ausprägung der Variablen „Subjektive Schichteinstufung“ ergibt sich für die abhängige Variable „Wahlabsicht Bundestagswahl“ der Vorhersagewert „CDU/CSU“ (Kategorie: Mittelschicht, Obere Mittelschicht/Oberschicht), „SPD“ (Kategorie: Arbeiterschicht) oder „Andere Partei/Nichtwähler“ (alle anderen Kategorien). Der Vorhersagefehler und .
Das heißt, im vorliegenden Beispiel kann der Fehler bei der Vorhersage der Wahlabsicht der Bundestagswahl des Befragten um 3,1 % reduziert werden, wenn man seine eigene subjektive Schichteinstufung kennt.
Goodman und Kruskals τ[Bearbeiten | Quelltext bearbeiten]
Bei Goodman und Kruskals wird als Vorhersagewert statt der Modalkategorie ein zufälliger gezogener Wert aus der Verteilung von Y angenommen, d. h. mit Wahrscheinlichkeit wird Kategorie 1 gezogen, mit Wahrscheinlichkeit wird Kategorie 2 gezogen und so weiter. Der Vorhersagefehler ergibt sich dann als
mit die absolute Häufigkeit der Kategorie der abhängigen Variablen. Analog ergibt sich der Vorhersagefehler , nur dass jetzt die Vorhersage entsprechend für jede Kategorie der unabhängigen Variablen gemacht wird und der Vorhersagefehler ergibt sich als Summe der gewichteten Vorhersagefehler in jeder Kategorie der unabhängigen Variablen.
mit die absolute Häufigkeit für das gemeinsame Auftreten der Kategorien und .
Symmetrische Maße[Bearbeiten | Quelltext bearbeiten]
Für Goodman und Kruskals und können die Vorhersagefehler
- und , wenn die abhängige Variable ist, und
- und , wenn die abhängige Variable ist,
berechnet werden. Die symmetrischen Maße für Goodman und Kruskals und ergeben sich dann als
- .
Unsicherheitskoeffizient[Bearbeiten | Quelltext bearbeiten]
Entropie[Bearbeiten | Quelltext bearbeiten]
Der Unsicherheitskoeffizient misst die Unsicherheit der Information mit Hilfe der Entropie. Wenn die relative Häufigkeit des Auftretens der Kategorie ist, dann ist die Entropie oder Unsicherheit definiert als
Die Unsicherheit ist Null, wenn für alle möglichen Kategorien bis auf eine ist. Die Vorhersage, welchen Kategorienwert eine Variable annimmt, ist dann trivial. Ist (Gleichverteilung), dann ist die Unsicherheit und auch maximal.
Asymmetrischer Unsicherheitskoeffizient[Bearbeiten | Quelltext bearbeiten]
Das Fehlermaß unter Unkenntnis des Zusammenhangs ist daher die Unsicherheit für die abhängige Variable
Das Fehlermaß unter Kenntnis des Zusammenhangs ist die gewichtete Summe der Unsicherheit für jede Kategorie der abhängigen Variablen
Dieser Ausdruck lässt auch schreiben als
mit die Unsicherheit basierend auf der gemeinsamen Verteilung von und und die Unsicherheit der unabhängigen Variable .
Der Unsicherheitskoeffizient ergibt sich dann als
Symmetrischer Unsicherheitskoeffizient[Bearbeiten | Quelltext bearbeiten]
Für den Unsicherheitskoeffizient können die Vorhersagefehler
- und , wenn die abhängige Variable ist, und
- und , wenn die abhängige Variable ist,
berechnet werden. Der symmetrische Unsicherheitskoeffizient ergibt sich, wie bei Goodman and Kruskals und , als
- .
Goodman und Kruskals γ[Bearbeiten | Quelltext bearbeiten]
sei die Zahl konkordanten Paare ( und ) und die Zahl diskordanten Paare ( und ). Wenn wir keine gemeinsamen Rangzahlen (Ties) haben und die Anzahl der Beobachtungen ist, dann gilt .
Unter Unkenntnis des Zusammenhangs können wir keine Aussage darüber machen, ob ein Paar konkordant oder diskordant ist. Daher sagen wir Wahrscheinlichkeit 0,5 ein konkordantes bzw. diskordantes Paar vorher. Der Gesamtfehler für alle möglichen Paare ergibt sich als
Unter Kenntnis des Zusammenhangs wird immer Konkordanz vorhergesagt, falls , oder immer Diskordanz, wenn . Der Fehler ist
und es folgt
Der Betrag von Goodman and Kruskals ist damit ein symmetrisches proportionales Fehlerreduktionsmaß.
η2[Bearbeiten | Quelltext bearbeiten]

Wie bei dem Bestimmtheitsmaß ist der Vorhersagewert für die abhängige metrische Variable unter Unkenntnis des Zusammenhangs und der Vorhersagefehler
- .
Bei Kenntnis, zu welcher der Gruppen der nominale oder ordinale unabhängigen Variable die Beobachtung gehört, ist der Vorhersagewert gerade der Gruppenmittelwert . Der Vorhersagefehler ergibt sich als
mit , wenn die Beobachtung zur Gruppe gehört und sonst Null. Damit ergibt sich
- .
Die Rollen der abhängigen und unabhängigen Variablen können nicht vertauscht werden, da sie unterschiedliche Skalenniveaus haben. Deswegen gibt es nur ein (asymmetrisches) Maß.
In Cohen (1988)[1] wird als Daumenregel angegeben:
- kein Zusammenhang,
- geringer Zusammenhang,
- mittlerer Zusammenhang und
- starker Zusammenhang.
Beispiel
In dem Beispiel kann der Fehler bei der Vorhersage des Nettoeinkommens bei Kenntnis der Schichteinstufung um , also knapp 10 %, reduziert werden. Das zweite ergibt sich, wenn man die Rolle der Variablen vertauscht, was aber hier unsinnig ist. Daher muss dieser Wert ignoriert werden.
Literatur[Bearbeiten | Quelltext bearbeiten]
- Y.M.M. Bishop, S.E. Feinberg, P.W. Holland (1975). Discrete Multivariate Analysis: Theory and Practice. Cambridge, MA: MIT Press.
- L.C. Freemann (1986). Order-based Statistics and Monotonicity: A Family of Ordinal Measures of Association. Journal of Mathematical Sociology, 12(1), S. 49–68
- J. Bortz (2005). Statistik für Human- und Sozialwissenschaftler (6. Auflage), Springer Verlag.
- B. Rönz (2001). Skript "Computergestützte Statistik II", Humboldt-Universität zu Berlin, Lehrstuhl für Statistik.
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ a b J. Cohen (1988). Statistical Power Analysis for Behavioral Science. Erlbaum, Hilsdale.
- ↑ a b c L.A. Goodman, W.H. Kruskal (1954). Measures of association for cross-classification. Journal of the American Statistical Association, 49, S. 732–764.
- ↑ H. Theil (1972), Statistical Decomposition Analysis, Amsterdam: North-Holland Publishing Company (diskutiert den Unsicherheitskoeffizient).























































![{\displaystyle E_{2}=\sum _{j}{\frac {h_{\bullet ,j}}{n}}\underbrace {\left[-\sum _{k}{\frac {h_{k,j}}{h_{\bullet ,j}}}\log \left({\frac {h_{k,j}}{h_{\bullet ,j}}}\right)\right]} _{\begin{matrix}{\text{Unsicherheit in Kategorie }}j\\{\text{der unabhängigen Variable}}\end{matrix}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c7b4e5d0cb0e668e48387ccf0a35e5b29bb4203)
![{\displaystyle E_{2}=U_{XY}-U_{X}=\left[-\sum _{j,k}{\frac {h_{k,j}}{n}}\log \left({\frac {h_{k,j}}{n}}\right)\right]-\left[-\sum _{j}{\frac {h_{\bullet ,j}}{n}}\log \left({\frac {h_{\bullet ,j}}{n}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40a92eda0a1e1657562d4ab4cbd259a3a41a53a1)


























