Morse-Theorie

Die Morse-Theorie aus dem Bereich der Differentialtopologie gibt einen sehr direkten Zugang zur Analyse der Topologie einer Mannigfaltigkeit über das Studium differenzierbarer Funktionen auf dieser Mannigfaltigkeit. Die wesentlichen Einsichten dazu verdankt man dem US-amerikanischen Mathematiker Marston Morse.

Die Theorie erlaubt es, CW-Strukturen (oder CW-Komplexe nach John Henry Constantine Whitehead) und Henkelzerlegungen (handle-decomposition) der Mannigfaltigkeit zu finden und so Informationen über deren Homologie zu erhalten.

Davor hatten schon im 19. Jahrhundert Arthur Cayley und James Clerk Maxwell einige dieser Konzepte aus der Betrachtung topographischer Karten gewonnen (Bergsteigerformel). Morse wandte seine Theorie ursprünglich auf geodätische Kurven an (kritische Punkte des Energiefunktionals auf Wegen). Die Techniken der Morse-Theorie wurden in Raoul Botts berühmtem Beweis seines Periodizitätssatzes für die stabilen Homotopiegruppen der unitären, orthogonalen und symplektischen Gruppe benutzt.

Grundlegende Konzepte

Ein Sattelpunkt

Man betrachte für Anschauungszwecke eine bergige Landschaft M. Wenn $f\colon M\to \mathbb {R}$ die Höhenfunktion (später Morse-Funktion genannt) ist, die jedem Punkt seine Höhe zuordnet, dann ist das Umkehrbild eines Punktes in $\mathbb {R}$ (die Niveaumenge) einfach eine Konturlinie. Jeder zusammenhängende Teil einer Konturlinie ist entweder ein Punkt, eine einfache geschlossene Kurve oder eine geschlossene Kurve mit Doppelpunkt (Knoten). Konturlinien können auch Punkte höherer Ordnung (Dreifachpunkte usw.) haben, aber diese sind instabil und können durch leichte Deformation von M beseitigt werden. Doppelpunkte in Konturlinien kommen bei Sattelpunkten vor (oder Pässen). Dort verlaufen die umliegenden Konturlinien einmal aufwärts und in anderer Richtung abwärts.

Nun stelle man sich vor, die Landschaft würde mit Wasser geflutet. Erreicht dieses eine Höhe $a$ ist die durch das Wasser bedeckte Fläche (die Punkte mit Höhe $\leq a$) gleich $f^{-1}\left(-\infty ,a\right]$. Wie ändert sich die Topologie der Region, wenn das Wasser steigt? Intuitiv ändert sie sich nur, falls $a$ die Höhe eines kritischen Punktes passiert. Das ist ein Punkt, an dem die Ableitung (Gradient) von f verschwindet. Mit anderen Worten, die Topologie ändert sich nur, falls das Wasser beginnt (1) ein Becken zu füllen (Minimum), (2) einen Sattel (Bergpass) zu überdecken, oder (3) einen Gipfel (Maximum) zu überfluten.

Der Torus

Jedem dieser drei Typen von kritischen Punkten – Minima, Maxima, Sattelpunkten – ordnet man eine Zahl, den Index, zu (Morseindex). Grob gesagt ist das die Zahl der unabhängigen Richtungen um den Punkt, auf denen die Funktion f abnimmt. Das ist für Minima 0, Sattelpunkte 1, Maxima 2.

$M^{a}$ sei als $f^{-1}\left(-\infty ,a\right]$ definiert. Eine ähnliche Untersuchung darüber, wie sich die Topologie von $M^{a}$ ändert, wenn $a$ zunimmt, kann man für einen Torus $M$ anstellen, der wie auf dem Bild angeordnet sei, wobei $f$ die Projektion auf die vertikale Achse ist.

Diese Figuren sind homotopieäquivalent

Diese Figuren sind homotopieäquivalent

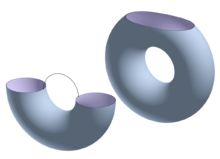
Hier gibt es 4 kritische Punkte $p,q,r$ und $s$. Die Punkte $p$ und $s$ sind der Süd- bzw. Nordpol des Torus, $q$ und $r$ sind Süd- bzw. Nordpol des Loches im Torus. Wenn $a$ kleiner als Null ist, ist $M^{a}$ leer. Nachdem $a$ die Höhe von $p$ (einem kritischen Punkt mit Index 0) passiert hat, mit $0<a<f(q)$, ist $M^{a}$ eine Scheibe, die also homotopieäquivalent zu einem Punkt ist. Dort wird eine 0-Zelle an die leere Menge „angehängt“. Passiert $a$ die Höhe von $q$ (einem kritischen Punkt vom Index 1), mit $f(q)<a<f(r)$, ist $M^{a}$ ein Zylinder, homotopieäquivalent zu einer Scheibe mit angehängter 1-Zelle (s. Bild links). Passiert $a$ die Höhe von $r$ (kritischer Punkt mit Index 1), mit $f(r)<a<f(s)$, ist $M^{a}$ ein Torus, dem eine Scheibe entfernt wurde, homotopieäquivalent einem Zylinder mit angehängter 1-Zelle (Bild rechts). Passiert $a$ schließlich die Höhe von $s$ (ein kritischer Punkt vom Index 2), ist $M^{a}$ ein Torus, äquivalent dem Anheften einer 2-Zelle.

Es zeichnet sich also folgende Regel ab: die Topologie von $M_{\alpha }$ ändert sich nur, wenn $\alpha$ die Höhe eines kritischen Punktes passiert. Passiert $\alpha$ die Höhe eines kritischen Punktes mit Index γ, wird eine γ-Zelle an $M^{a}$ angehängt. Sind mehrere kritische Punkte auf gleicher Höhe, löst man die Situation durch Betrachtung einer kleinen Störung von $f$.

So wie sie hier formuliert ist, ist die Regel allerdings falsch. Zum Beweis sei $M$ gleich $\mathbb {R}$ und $f(x)=x^{3}$. Dann ist 0 ein kritischer Punkt von $f$, aber die Topologie von $M^{a}$ ändert sich nicht, wenn $\alpha$ Null passiert. Tatsächlich ist hier der Index schlecht definiert, da auch die zweiten Ableitungen in 0 verschwinden. Man spricht von einem ausgearteten kritischen Punkt. Bei Rotation des Koordinatensystems ist der kritische Punkt instabil – er verschwindet entweder oder zerfällt in zwei nichtausgeartete kritische Punkte.

Formale Entwicklung

Für eine reellwertige glatte Funktion $f\colon M\to \mathbb {R}$ auf einer differenzierbaren Mannigfaltigkeit $M$ werden die Punkte, auf denen die Ableitung von $f$ verschwindet, kritische Punkte von $f$ genannt, und ihre Bilder unter $f$ werden kritische Werte genannt. Falls bei einem kritischen Punkt $b$ die Matrix der zweiten partiellen Ableitungen (Hesse-Matrix) nicht singulär ist (das heißt, sie ist invertierbar), wird $b$ nichtausgearteter kritischer Punkt genannt (falls die Hesse-Matrix singulär ist analog ausgeartet)

Beispiel: Für die Funktionen

$f(x)=a+bx+cx^{2}+dx^{3}+\cdots$

von $\mathbb {R}$ nach $\mathbb {R}$ hat $f$ einen kritischen Punkt am Ursprung für $b=0$, der für $c\not =0$ nichtausgeartet ist ($f$ ist von der Form $a+cx^{2}+\ldots$) und für $c=0$ ausgeartet ist ($f$ ist von der Form $a+dx^{3}+\ldots$). Ein weniger triviales Beispiel ist der Affensattel.

Der Index eines nichtausgearteten kritischen Punktes $b$ von $f$ ist die Dimension des größten Unterraumes des Tangentialraumes zu $M$ bei $b$, auf dem die Hesse-Matrix negativ definit ist. Das entspricht der obigen intuitiven Definition als Anzahl der Richtungen, auf denen $f$ abnimmt.

Das Morse-Lemma

Sei $b$ ein nicht-ausgearteter kritischer Punkt von $f\colon M\to \mathbb {R}$. Dann gibt es eine Karte $(x_{1},\dots ,x_{n})$ in einer Umgebung $U$ von $b$, so dass $x_{i}(b)=0$ für alle $i$ und

$f(x)=f(b)-x_{1}^{2}-...-x_{\alpha }^{2}+x_{\alpha +1}^{2}+...+x_{n}^{2}$

in ganz $U$. Dabei ist α gleich dem Index von $f$ bei $b$. Als Korollar des Morse-Lemmas folgt, dass die nichtausgearteten kritischen Punkte isoliert sind.

Morse-Funktionen

Eine glatte reellwertige Funktion auf einer Mannigfaltigkeit $M$ ist eine Morse-Funktion, falls sie keine ausgearteten kritischen Punkte hat. Ein grundlegendes Resultat der Morse-Theorie besagt, dass fast alle Funktionen Morse-Funktionen sind. Präzise ausgedrückt bilden sie eine dichte offene Teilmenge im Raum aller glatten Funktionen $M\to \mathbb {R}$ in der $C^{2}$-Topologie. Man beschreibt diesen Sachverhalt auch mit Eine typische Funktion ist eine Morse-Funktion oder Eine generische Funktion ist Morse-Funktion.

Subniveaumengen

Wie gesagt ist man an der Frage interessiert, wie sich die Topologie von $M^{a}=f^{-1}(-\infty ,a]$ ändert, wenn $a$ variiert. Dies wird teilweise durch folgenden Satz beantwortet:

Satz

Es sei $f$ sei eine glatte reellwertige Funktion auf $M$, es sei $a<b$ und $f^{-1}[a,b]$ sei kompakt. Wenn es zwischen $a$ und $b$ keine kritischen Werte gibt, dann ist $M^{a}$ diffeomorph zu $M^{b}$, und $M^{b}$ ist ein Deformationsretrakt auf $M^{a}$.

Weiter interessiert, wie sich die Topologie von $M^{a}$ ändert, wenn $a$ einen kritischen Wert passiert. Dazu gilt folgender Satz:

Satz

Es sei $f$ sei eine glatte reellwertige Funktion auf $M$ und $p$ sei ein nichtausgearteter kritischer Punkt von $f$ mit Index $\gamma$. Weiter sei $f(p)=q$ und $f^{-1}[q-\epsilon ,q+\epsilon ]$ sei kompakt und enthalte keine kritischen Punkte außer $p$. Dann ist für genügend kleine $\epsilon$ die Menge $M^{q+\epsilon }$ homotopieäquivalent zu $M^{q-\epsilon }$ mit einer angehängten $\gamma$-Zelle.

Diese Resultate verallgemeinern und präzisieren die (in der dortigen Form inkorrekte) Regel aus dem vorherigen Abschnitt.

Mit den zwei vorherigen Resultaten und der Tatsache, dass auf jeder differenzierbaren Mannigfaltigkeit eine Morse-Funktion existiert, kann man zeigen, dass jede differenzierbare Mannigfaltigkeit ein CW-Komplex ist, mit einer $n$-Zelle für jeden kritischen Punkt mit Index $n$. Dazu muss man zeigen, dass man die kritischen Punkte so anordnen kann, dass auf jeder kritischen Höhe nur ein kritischer Punkt ist.

Die Morse-Ungleichungen

Die Morse-Theorie kann dazu benutzt werden, die Homologie einer Mannigfaltigkeit stark einschränkende Sätze zu beweisen. Die Zahl der kritischen Punkte mit Index $\gamma$ von $f\colon M\to \mathbb {R}$ ist gleich der Zahl der $\gamma$-Zellen in der CW Struktur von $M$, die man durch „Erklettern“ von $f$ erhält. Da die alternierende Summe der Ränge der Homologiegruppen eines topologischen Raumes gleich der alternierenden Summe des Ranges der Kettenkomplexgruppen ist, mit denen die Homologie berechnet wird, sieht man, dass die Euler-Charakteristik gleich der Summe

$\sum (-1)^{\gamma }C^{\gamma }\,$

ist, wobei $C^{\gamma }$ die Zahl der kritischen Punkte mit Index $\gamma$ ist. Aus der Homologietheorie ist weiter bekannt, dass der Rang der $n$-ten Homologiegruppe eines CW-Komplexes $M$ kleiner oder gleich der Anzahl der $n$-Zellen in $M$ ist. Der Rang der $\gamma$^ten Homologiegruppe ist also kleiner oder gleich der Anzahl der kritischen Punkte vom Index $\gamma$ einer Morse-Funktion auf $M$. Das lässt sich in den Morseungleichungen präzisieren:

$C^{\gamma }-C^{\gamma -1}+-\cdots \pm C^{0}\geq {\rm {Rank}}[H_{\gamma }(M)]-{\rm {Rank}}[H_{\gamma -1}(M)]+-\cdots \pm {\rm {Rank}}[H_{0}(M)]$

Morse-Homologie

Morse-Homologie ist durch eine generische Wahl der Morse-Funktion und der riemannschen Metrik definiert. Das grundlegende Resultat ist, dass diese Homologie unabhängig von dieser Wahl ist, also eine Invariante der Mannigfaltigkeit, und isomorph zur singulären Homologie ist. Daraus folgt, dass die Morse-Zahlen und (singulären) Betti-Zahlen übereinstimmen, was einen unmittelbaren Beweis der Morse-Ungleichungen ergibt. Eine unendlich-dimensionale Variante der Morse-Homologie ist als Floer-Homologie bekannt.

Edward Witten entwickelte 1982 einen weiteren Zugang zur Morse-Theorie mit harmonischen Funktionen und Supersymmetrie.

Morse-Bott-Theorie

Der Begriff der Morse-Funktion kann auf Funktionen mit nicht-ausgearteten kritischen Mannigfaltigkeiten erweitert werden, das heißt, der Kern der Hessematrix am kritischen Punkt ist gleich dem Tangentialraum der kritischen Untermannigfaltigkeit. Falls diese Punkte sind, ergibt sich wieder der klassische Fall der Morse-Funktion. Der Index wird am natürlichsten als Paar

$(i_{-},i_{+}),$

definiert, wobei $i_{-}$ die Dimension der instabilen Mannigfaltigkeit an einem gegebenen Punkt der kritischen Mannigfaltigkeit ist, und $i_{+}$ gleich $i_{-}$ plus der Dimension der kritischen Mannigfaltigkeit ist. Bei kleiner Störung der Morse-Bott-Funktion liegen die Indices der neuen Funktion zwischen $i_{-}$ und $i_{+}$ auf der ungestörten kritischen Mannigfaltigkeit.

Morse-Bott-Funktionen sind nützlich, da man mit typischen (generischen) Morse-Funktionen schwer arbeiten kann. Die visualisierbaren und gut berechenbaren Funktionen haben typischerweise Symmetrien und führen oft zu kritischen Mannigfaltigkeiten positiver Dimension. Raoul Bott benutzte die Morse-Theorie in dem ursprünglichen Beweis seines Periodizitätssatzes.

Auch die Morse-Homologie kann für Morse-Bott-Funktionen definiert werden. Das Differential in dieser Homologie wird durch eine Spektralsequenz berechnet. Frederic Bourgeois entwickelte einen solchen Zugang im Rahmen seiner Morse-Bott-Version der symplektischen Feldtheorie, die jedoch aufgrund erheblicher analytischer Probleme nicht publiziert wurde.

Literatur

• Raoul Bott: Morse Theory indomitable. In: Publications Mathématiques de l'IHES. 68, 1988, S. 99, online bei [1].
• Raoul Bott: Lectures on Morse theory, old and new. In: Bulletin of the American Mathematical Society. 7, 1982, S. 331, Online.
• Arthur Cayley: On Contour and Slope Line. In: The Philosophical Magazine. 18, 1859, S. 264–268.
• Yukio Matsumoto: An Introduction to Morse Theory. American Mathematical Society, Providence RI 2002, ISBN 0-8218-1022-7 (Translations of Mathematical Monographs. 208 = Iwanami Series in modern Mathematics).
• James Clerk Maxwell: On Hills and Dales. In: The Philosophical Magazine. 40, 1870, S. 269, online bei: On Hills and Dales (PDF; 803 kB).
• J. Milnor: Morse theory. Based on Lecture Notes by M. Spivak and R. Wells. Princeton University Press, Princeton NJ 1963 (Annals of Mathematics Studies 51, ISSN 0066-2313).
• John Milnor: Lectures on the h-Cobordism theorem. Princeton University Press, Princeton NJ 1965 (Mathematical Notes 1).
• Marston Morse: The Calculus of Variations in the Large. American Mathematical Society, New York NY 1934 (American Mathematical Society. Colloquium Publications. 18, ISSN 0065-9258).
• Matthias Schwarz: Morse Homology. Birkhäuser, Basel u. a. 1993, ISBN 3-7643-2904-1 (Progress in Mathematics 111).
• H. Seifert, W. Threlfall: Variationsrechnung im Grossen. (Theorie von Marston Morse). = Morsesche Theorie. Teubner, Leipzig u. a. 1938 (Hamburger mathematische Einzelschriften 24, ZDB-ID 503145-x).

Weblinks

• Seminar Morsetheorie von Schick, Göttingen, Vortrag Hage zur Einführung in die Morsetheorie, pdf
• Conrad, Skript zu Morse-Lemma, pdf