Stern-Gerlach-Versuch

Mit Hilfe des Stern-Gerlach-Versuchs von 1922 wurde von den Physikern Otto Stern[1] und Walther Gerlach[2] erstmals die Richtungsquantelung von Drehimpulsen beobachtet. Der Stern-Gerlach-Versuch ist ein grundlegendes Experiment in der Physik und wird immer wieder herangezogen, um diese quantenmechanische Erscheinung zu erläutern, die im Rahmen der klassischen Physik nicht verständlich ist.[3]
Beschreibung[Bearbeiten | Quelltext bearbeiten]

Ein Strahl von (elektrisch neutralen) Silberatomen durchfliegt im Vakuum den Spalt zwischen den Polschuhen eines Magneten. Der eine Polschuh hat die Form einer zum Strahl parallelen Schneide, der andere die einer flachen Rinne. Dadurch ist das Magnetfeld in der Richtung quer zum Strahl stark inhomogen. Nachdem der Strahl das Magnetfeld durchlaufen hat, schlagen sich die Silberatome auf einer Glasplatte nieder. Es werden zwei voneinander getrennte Flecke gefunden, das heißt, das Magnetfeld spaltet den Strahl in zwei getrennte Teilstrahlen auf.[4]
Erklärung[Bearbeiten | Quelltext bearbeiten]
Das Silberatom hat ein magnetisches Dipolmoment bestimmter Größe, auf das im inhomogenen Feld eine Kraft wirkt:
(Dabei ist die Feldrichtung als -Achse gewählt, in der Abbildung: die senkrechte Richtung.) Je nach Größe der -Komponente des magnetischen Moments, d. h. je nach Anstellwinkel zur Feldrichtung, erfahren die verschiedenen Atome Kräfte verschiedener Größe parallel oder antiparallel zur Feldrichtung. Klassisch erwartet man daher eine kontinuierliche Aufweitung des Strahls in -Richtung.
Das magnetische Moment rührt von dem Drehimpuls des Atoms her und ist zu ihm parallel. Der Drehimpuls mit der Quantenzahl ½ hat in -Richtung nur die Einstellmöglichkeiten oder , entsprechend der Einstellung entweder parallel oder antiparallel zur z-Achse ( ist die reduzierte Planck-Konstante). Im klassischen Bild entspricht das einer rotierenden geladenen Kugel, die um die z-Achse mit gleicher Rotationsgeschwindigkeit je nach Vorzeichen links- bzw. rechtsherum rotiert. Allerdings könnte im klassischen Bild der Drehimpulsvektor jeden beliebigen Winkel mit der z-Achse bilden.
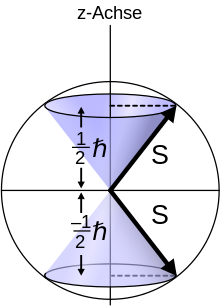
Da parallel zu ist, kann auch , die -Komponente von , nur einen bestimmten positiven oder einen gleich großen negativen Wert annehmen. Deshalb wirkt auf jedes Atom je nach Ausrichtung des Drehimpulses eine betragsmäßig gleiche, aber in der Richtung entgegengesetzte Kraft quer zur Flugrichtung. Der Strahl spaltet sich in zwei Teilstrahlen auf, so dass die beobachtete Verteilung entsteht.
Besonderheit des Silberatoms[Bearbeiten | Quelltext bearbeiten]
Grundsätzlich wird das magnetische Moment eines Atoms von der Gesamtheit der Bahndrehimpulse sowie der Spins aller seiner Elektronen gebildet (siehe Landé-Faktor eines Atoms; der Beitrag des Atomkerns ist vernachlässigbar klein.) Im Silberatom trägt jedoch nur das 5-Elektron zum magnetischen Moment bei, denn alle anderen Elektronen bilden abgeschlossene Schalen mit Drehimpuls Null. Das 5-Elektron hat die Bahndrehimpulsquantenzahl (es besitzt keinen Bahndrehimpuls). Der Gesamtdrehimpuls besteht also nur aus dem Spin dieses einen Elektrons, und das ganze Silberatom verhält sich wie ein einzelnes Spin-1/2-Teilchen. Da es elektrisch neutral ist, wird es, im Unterschied zum freien Elektron, im Versuch durch die im Magnetfeld herrschende Lorentzkraft oder durch elektrische Störfelder nicht abgelenkt.
Geschichte[Bearbeiten | Quelltext bearbeiten]
Eine Quantelung der Beträge von Bahndrehimpulsen von Elektronen im Atom hatte Niels Bohr 1913 postuliert (was von Otto Stern damals noch für „Unsinn“ gehalten wurde).[5] Die Quantelung des Einstellwinkels zu einem Magnetfeld war von Peter Debye[6][7] und Arnold Sommerfeld[8][9] 1916 im Rahmen der theoretischen Untersuchung des Zeemaneffekts vorhergesagt worden. Auch dieser Idee stand Stern skeptisch gegenüber, sah aber die Möglichkeit, das Bohrsche Atommodell mithilfe von Atomstrahlen zu überprüfen, wie sie seit 1911 von Louis Dunoyer de Segonzac experimentell erzeugt worden waren. Walter Gerlach hatte in Tübingen mit Atomstrahlen optische Experimente durchgeführt und wurde, als er nach Frankfurt ging, gleich bei seiner Ankunft im Herbst 1920 von Max Born und Otto Stern zu den dortigen Atomstrahlversuchen hinzugezogen. Stern hatte 1921 einen Versuch zum Nachweis der Richtungsquantelung vorgeschlagen[10]. Die Durchführung des Versuchs war schwierig, auch weil in der Inflationszeit die finanziellen Mittel fehlten. Max Born stellte aber Geld aus seinen Vorträgen über die Relativitätstheorie zur Verfügung, und Fritz Haber ermutigte die Experimentatoren und unterstützte sie mit Mitteln der Hoshi-Stiftung. Über Albert Einstein, den Born verständigt hatte, kam Geld für die Beschaffung des starken Magneten. Die Firma Messer spendete die flüssige Luft, mit der der Glasplatten-Detektor gekühlt wurde, und der amerikanische Bankier Henry Goldman (einer der Gründer der Bank Goldman Sachs), 400 Dollar.[5] Unterstützt wurden Stern und Gerlach vom Mechanikermeister Adolf Schmidt (1893–1971). Das Experiment selbst war ebenfalls schwierig. Die Apparatur war sehr kompakt aufgebaut (die Länge betrug nur rund zehn Zentimeter), wobei dem über 1000 Grad heißen Silberofen auf einer Seite die gekühlte Glasplatte zur Detektion auf der anderen Seite gegenüberstand. Es gab immer wieder Probleme mit den Vakuumpumpen, mit der Ausrichtung des Atomstrahls längs des Magneten, und die Blende für den Atomstrahl verklebte häufig mit Silber.[5] Die Experimentatoren hatten Silber aus praktischen Gründen wegen der leichten Nachweismöglichkeit gewählt (Der Silber-Niederschlag auf einer Glasplatte konnte mit Hilfe einer schwefelhaltigen Substanz schon in geringsten Mengen als schwarze Ablagerung sichtbar gemacht werden). Stern soll aus Erfahrung mit seinen billigen, schwefelhaltigen Zigarren, die er auch während des Experimentierens rauchte, auf die Idee der Verwendung von Silber gekommen sein.[5]
Die Frage, ob überhaupt ein quantenmechanischer Effekt mit dem Experiment beobachtet werden könne, wurde vielfach diskutiert und war umstritten, auch wegen der technischen Schwierigkeiten. Born und Niels Bohr glaubten daran, Debye nicht; Sommerfeld glaubte, nur ein halbklassischer Effekt wäre beobachtbar. Gerlach und Stern selbst waren offen hinsichtlich des Versuchsergebnisses. Allerdings erwartete Stern eher einen klassischen Effekt, wie Gerlach berichtet.[11]
Der Versuch wurde im Februar 1922 durch Gerlach im Gebäude des Physikalischen Vereins in Frankfurt am Main in der Robert-Mayer-Straße durchgeführt, nach Horst Schmidt-Böcking (nach erhaltenen Wetterbeschreibungen vom Tag des Experiments) in der Nacht vom 7. auf den 8. Februar.[12] Das Ergebnis überraschte besonders durch die Aufspaltung des Atomstrahls in gerader Anzahl, denn die zur Erklärung einer geraden Anzahl nötigen „halbzahligen“ Drehimpulse waren damals noch nicht bekannt. Stern und Gerlach hatten bereits nachgewiesen, dass das Silberatom in seinem Grundzustand ein von Null verschiedenes magnetisches Moment hat. Ihre wenig später durchgeführte genaue Messung dieses magnetischen Moments[13] ergab den erwarteten Betrag, 1 bohrsches Magneton, wie im Bohr-Sommerfeldschen Atommodell von einem Elektron mit einer Bahndrehimpulsquantenzahl vorhergesagt. Daher wäre eine Aufspaltung in Teilstrahlen zu erwarten gewesen, aber der erwartete unabgelenkte mittlere Teilstrahl trat nicht auf.
Gerlach teilte das Ergebnis Stern, der gerade in Rostock war, in einem Telegramm mit den Worten mit: Bohr hat doch Recht.[14] Wolfgang Pauli gab in seinem Glückwunschtelegramm an Gerlach vom 17. Februar 1922 zudem der Hoffnung Ausdruck, dass nun auch Stern von der Richtungsquantelung überzeugt sein würde.[14]
Die Richtungsquantelung als realer, beobachtbarer Effekt war mit dem Experiment erwiesen. Die Deutung des Experiments musste jedoch korrigiert werden, als 1925 der Begriff des Elektronenspins eingeführt worden war (Samuel Goudsmit, George Uhlenbeck). Die Aufspaltung der Silberatomstrahlen erfolgt tatsächlich wegen des magnetischen Moments des einzelnen äußeren Elektrons, obwohl dessen Bahndrehimpuls gleich Null ist und nicht dazu beiträgt. Der Erste, der die Aufspaltung auf ein magnetisches Eigenmoment des Elektrons zurückführte, war 1923 Alfred Landé. Landé übersah dabei, dass auch ein Eigendrehimpuls des Elektrons dahinter steht und ließ sich damit die Entdeckung des Elektronenspin entgehen.[5] 1927 führten Phipps und Taylor das Stern-Gerlach-Experiment mit Wasserstoffatomen aus und erhielten ebenfalls zwei Teilstrahlen.[15]
Albert Einstein äußerte sich 1922 so:[16] Das Interessanteste aber ist gegenwärtig das Experiment von Stern und Gerlach. Die Einstellung der Atome ohne Zusammenstöße ist nach den jetzigen Überlegungs-Methoden durch Strahlung nicht zu verstehen; eine Einstellung sollte von Rechts wegen mehr als 100 Jahre dauern. Ich habe mit Ehrenfest eine kleine Rechnung darüber angestellt. Rubens hält das experimentelle Ergebnis für absolut sicher.
Die Originalapparaturen sind im Zweiten Weltkrieg fast vollständig zerstört worden. Eine Rekonstruktion des Experiments durch Horst Schmidt-Böcking mit einigen erhaltenen Originalteilen – einem Mikroskop aus dem Besitz von Stern (2009 durch eine Nichte von Stern an Schmidt-Böcking übergeben) und Vakuumpumpen – wurde 2014 auf einer Jubiläumsausstellung der Universität Frankfurt gezeigt.[1]
Stern und Gerlach wurden für das Experiment mehrfach für den Nobelpreis vorgeschlagen (82[17] Nominierungen für Stern, 30[18] für Gerlach). Im Verlauf der Nobelpreis-Nominierungen verschob sich der Fokus vermehrt auf Stern, der z. B. als der „führende Geist der Untersuchungen“ genannt wurde.[19]
Als der Nobelpreis 1944 (rückwirkend für das Jahr 1943) an Stern verliehen wurde, wurde er nicht mit dem Stern-Gerlach-Versuch begründet,[20] sondern mit Sterns Beitrag zur Entwicklung der Molekularstrahl-Methode und seine Entdeckung des magnetischen Moments des Protons.[21] Das Stern-Gerlach-Experiment wurde allerdings in einer Würdigung durch Nobelpreis-Komiteemitglied Erik Hulthén in der Präsentation der Nobelpreisverleihung im schwedischen Radio am 10. Dezember 1944 hervorgehoben.[22] Obwohl Gerlach 30-mal für den Nobelpreis vorgeschlagen worden war, zuletzt 1944 durch das einflussreiche Nobelpreiskomitee-Mitglied Manne Siegbahn, wurde er bei der Preisvergabe übergangen, wahrscheinlich wegen seiner herausragenden Rolle in der deutschen physikalischen Forschung in der Zeit des Zweiten Weltkriegs.[23]
Anwendung[Bearbeiten | Quelltext bearbeiten]
Jeder der beiden Teilstrahlen im Stern-Gerlach-Versuch ist polarisiert. Daher findet das Prinzip des Versuchs Anwendung in manchen Quellen zur Erzeugung eines polarisierten Strahls von Ionen – meist Protonen oder Deuteronen – für Teilchenbeschleuniger. Der Atomstrahl durchläuft dabei statt des Dipolmagneten einen Quadrupol- oder Sextupolmagneten. Ein solcher Magnet fokussiert Atome mit einer der beiden Drehimpulsstellungen zur Mitte auf seine Achse, während er die anderen Atome defokussiert, also nach außen zerstreut. Aus den fokussierten Atomen lässt sich durch Stoßionisation in einem schwachen äußeren Magnetfeld durch Ausnützen der Hyperfeinaufspaltung ein polarisierter Ionenstrahl gewinnen.[24][25]
Der Versuch mit anderen Teilchen[Bearbeiten | Quelltext bearbeiten]
Atome[Bearbeiten | Quelltext bearbeiten]
Ein Strahl diamagnetischer Atome zeigt zunächst keine Aufspaltung, da deren Elektronenhüllen kein magnetisches Moment aufweisen. Bei sehr hoher Auflösung erkennt man aber eine Aufspaltung, die durch den Kernspin mit seinem viel kleineren magnetischen Moment verursacht wird. Bei paramagnetischen Atomen wird jede durch die Elektronenhülle verursachte Aufspaltung durch das magnetische Moment des Kerns weiter aufgespalten.[26]
Neutronen[Bearbeiten | Quelltext bearbeiten]
Die Strahlaufspaltung im inhomogenen Magnetfeld ist gelegentlich mit Erfolg verwendet worden, um die Polarisation eines Strahls langsamer Neutronen zu messen.[27][28]
Geladene Teilchen[Bearbeiten | Quelltext bearbeiten]
Ein Stern-Gerlach-Versuch mit geladenen Teilchen, etwa freien Elektronen, wird meist als unmöglich angesehen, weil die Lorentzkraft auf die Ladung sehr viel größer ist als die Kraft auf das magnetische Moment; schon die Querabmessungen des Strahls sowie kleine Geschwindigkeitsunterschiede würden wegen des inhomogenen Feldes zu einer Verschmierung führen, die die spinbedingte Aufspaltung überdeckt. Diese Aussage ist 1997 durch Batelaan u. M. aus theoretischer Sicht bezweifelt worden. Sie halten es für grundsätzlich möglich, einen Polarisator für Elektronenstrahlen nach dem Prinzip des Stern-Gerlach-Versuchs zu bauen.[29] Andere Forscher haben diesen Überlegungen widersprochen.[29][30]
Für Protonen oder andere Ionen liegt eine solche Möglichkeit noch ferner als für Elektronen, weil ihr magnetisches Moment um zwei bis drei Zehnerpotenzen kleiner ist.[31]
Siehe auch[Bearbeiten | Quelltext bearbeiten]
Literatur[Bearbeiten | Quelltext bearbeiten]
- Wolfgang Trageser: Der Stern-Gerlach-Versuch - Genese, Entwicklung und Rekonstruktion eines grundlegenden Experimentes der Quantentheorie 1916 bis 1926, Springer, 2022. ISBN 978-3-662-64198-9. doi:10.1007/978-3-662-64199-6
- Gerthsen, Kneser, Vogel: Physik. Springer-Verlag, 15. Auflage, 1986, ISBN 3-540-16155-4, S. 615–616
- H. Haken, H. Chr. Wolf: Atom- und Quantenphysik. 8. Auflage, Springer 2004, ISBN 3-540-02621-5, Seite 196–197
- W. Demtröder: Atoms, Molecules and Photons. Springer, 2010, ISBN 978-3-642-10297-4, Seite 175–176
- Gerlach: Zur Entdeckung des Stern-Gerlach-Effekts, Physikalische Blätter, Band 25, 1969, S. 472. doi:10.1002/phbl.19690251008
- Casimir: Die Bedeutung des Stern-Gerlach-Experiments für die Entwicklung der Quantentheorie, Physikalische Blätter, Band 37, 1981, Nr. 3, S. 57–58. doi:10.1002/phbl.19810370303
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Bretislav Friedrich, Dudley Herschbach: Stern and Gerlach: How a Bad Cigar Helped Reorient Atomic Physics, Physics Today 56, 53-59 (2003). doi:10.1063/1.1650229
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ a b Stern, Otto (1888-1969) | Frankfurter Personenlexikon. 22. Oktober 2019, abgerufen am 29. Oktober 2021.
- ↑ Gerlach, Walther | Frankfurter Personenlexikon. 22. Oktober 2019, abgerufen am 29. Oktober 2021.
- ↑ Experiment in Physics > Appendix 5: Right Experiment, Wrong Theory: The Stern-Gerlach Experiment (Stanford Encyclopedia of Philosophy). Abgerufen am 29. Oktober 2021.
- ↑ Walther Gerlach und Otto Stern: Der experimentelle Nachweis der Richtungsquantelung im Magnetfeld. In: Zeitschrift für Physik. Band 9, 1922, S. 349–352, doi:10.1007/BF01326983.
- ↑ a b c d e Ulf von Rauchhaupt, Das Stern-Gerlach-Experiment, Frankfurter Allgemeine Sonntagszeitung, 6. Februar 2022, S. 54
- ↑ Debye, Quantenhypothese und Zeemaneffekt, Nachrichten Akad. Wiss. Göttingen, Math-Phys. Klasse, 1916. S. 142, und Physikalische Zeitschrift, Band 17, 1916, S. 507.
- ↑ P. Debye: Quantenhypothese und Zeemann-Effekt. In: Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse. Band 1916, 1916, S. 142–153 (eudml.org [abgerufen am 29. Oktober 2021]).
- ↑ Sommerfeld, Zur Theorie des Zeemaneffekts der Wasserstofflinien, mit einem Anhang über den Starkeffekt, Physikalische Zeitschrift, Band S. 17, 1916, S. 491–507
- ↑ Wolfgang Pauli: Sommerfelds Beiträge zur Quantentheorie. In: Physik und Erkenntnistheorie. Vieweg+Teubner Verlag, Wiesbaden 1984, ISBN 978-3-528-08563-6, S. 32–41, doi:10.1007/978-3-322-88799-3_5.
- ↑ Stern, Ein Weg zur experimentellen Prüfung der Richtungsquantelung im Magnetfeld, Z. f. Physik, Band 7, 1921, S. 249–253
- ↑ Gerlach, Erinnerungen an Albert Einstein 1908–1930, Physikalische Blätter Band 35, 1979, Heft 3, S. 97f
- ↑ Astrid Ludwig, Der vergessene Nobelpreisträger, Frankfurter Rundschau, 28. Dezember 2010, Horst Schmidt-Böcking über Otto Stern
- ↑ Walther Gerlach und Otto Stern: Das magnetische Moment des Silberatoms. In: Zeitschrift für Physik. Band 9, 1922, S. 353–355, doi:10.1007/BF01326984.
- ↑ a b Wolfgang Gentner, Gedenkworte für Walther Gerlach, Orden Pour le Mérite, Reden und Gedenkworte, Band 16, 1980, S. 47–53, Telegramm von Gerlach an Stern S. 48, Postkarte von Pauli S. 49
- ↑ T. E. Phipps, J. B. Taylor: The Magnetic Moment of the Hydrogen Atom. Physical Review Band 29 (1927) S. 309–320
- ↑ Einstein, Born, Briefwechsel, Langen-Müller, S. 102f, Brief Nr. 42 (ohne Datum)
- ↑ Nomination archive – Otto Stern. Nobel Prize Outreach AB, 1. April 2020, abgerufen am 29. Oktober 2021 (amerikanisches Englisch).
- ↑ Nomination archive – Walter Gerlach. 1. April 2020, abgerufen am 29. Oktober 2021 (amerikanisches Englisch).
- ↑ Otto Sterns gesammelte Briefe – Band 2. 2019, S. 293, doi:10.1007/978-3-662-58837-6.
- ↑ Daniel Kleppner: Our Enduring Legacy from Otto Stern. In: Molecular Beams in Physics and Chemistry. Springer International Publishing, Cham 2021, ISBN 978-3-03063962-4, S. 97–117, doi:10.1007/978-3-030-63963-1_7.
- ↑ The Nobel Prize in Physics 1943. Abgerufen am 29. Oktober 2021 (amerikanisches Englisch).
- ↑ Josef Georg Huber, Horst Schmidt-Böcking, Bretislav Friedrich: Walther Gerlach (1889–1979): Precision Physicist, Educator and Research Organizer, Historian of Science. In: Molecular Beams in Physics and Chemistry. Springer International Publishing, Cham 2021, ISBN 978-3-03063962-4, S. 119–161, doi:10.1007/978-3-030-63963-1_8.
- ↑ Horst Schmidt-Böcking, Alan Templeton, Wolfgang Trageser (Hrsg.), Otto Sterns Gesammelte Briefe, Band 2, Springer 2019, S. 344. Der Zusammenhang kann nach den Autoren aber nicht belegt werden.
- ↑ G. Clausnitzer, R. Fleischmann, H. Schopper, Zeitschrift für Physik Band 144 (1956) S. 336
- ↑ H. Paetz gen. Schieck: Nuclear Physics with Polarized Particles. Heidelberg usw.: Springer, 2012. ISBN 978-3-642-24225-0
- ↑ Gerthsen, Kneser, Vogel (siehe Literaturliste)
- ↑ S. Barkan et al.: Measurement of the Polarization of Thermal Neutron Beams of Mixed Velocities. Review of Scientific Instruments Bd. 39 (1968) S. 101. doi:10.1063/1.1683079
- ↑ J. E. Sherwood, T. E. Stephenson, Seymour Bernstein: Stern-Gerlach Experiment on Polarized Neutrons. In: Physical Review. Band 96, Nr. 6, 15. Dezember 1954, S. 1546–1548, doi:10.1103/PhysRev.96.1546.
- ↑ a b H. Batelaan, T. J. Gay, J. J. Schwendiman: Stern-Gerlach Effect for Electron Beams. In: Physical Review Letters. Band 79, Nr. 23, 8. Dezember 1997, S. 4517–4521, doi:10.1103/PhysRevLett.79.4517.
- ↑ George H. Rutherford, Rainer Grobe: Comment on Stern-Gerlach Effect for Electron Beams. In: Physical Review Letters. Band 81, Nr. 21, 23. November 1998, S. 4772–4772, doi:10.1103/PhysRevLett.81.4772.
- ↑ RW: Am Kern des Antimaterie-Rätsels. MPG, 28. Mai 2014, abgerufen am 29. Oktober 2021.













