Strassen-Algorithmus
Der Strassen-Algorithmus (erfunden vom deutschen Mathematiker Volker Strassen) ist ein Algorithmus aus der Linearen Algebra und wird zur Matrizenmultiplikation verwendet. Der Strassen-Algorithmus realisiert die Matrizenmultiplikation asymptotisch effizienter als das Standardverfahren und ist in der Praxis schneller für große Matrizen (solche mit einem Rang größer als 1000).
Der Algorithmus
[Bearbeiten | Quelltext bearbeiten]Vereinfachend wird der Spezialfall quadratischer Matrizen mit Zeilen bzw. Spalten betrachtet.
Seien also Matrizen über einem Ring und ferner ihr Produkt . Diese lassen sich auch als Blockmatrizen
betrachten, wobei sind.
Für die Multiplikation von Blockmatrizen gilt:
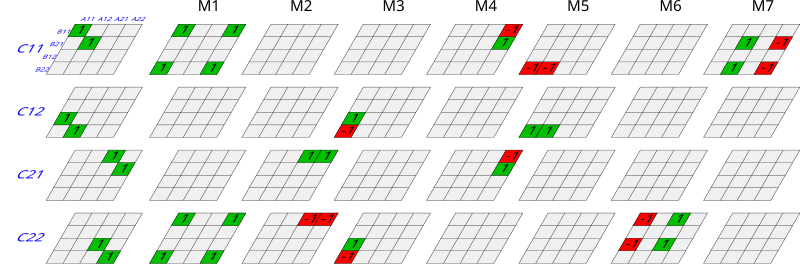
Die direkte Berechnung der benötigt also (aufwändige) Matrizenmultiplikationen. Um diese Anzahl zu reduzieren, berechnet der Algorithmus von Strassen folgende Hilfsmatrizen:
Zur Berechnung der sind lediglich Multiplikationen nötig, die lassen sich nun durch Additionen (und Subtraktionen) ermitteln:
Für die Multiplikationen in der Berechnung der wird obiges Verfahren rekursiv ausgeführt, bis das Problem auf die Multiplikation von Skalaren reduziert ist.
In der Praxis kann die gewöhnliche Multiplikation für kleine Matrizen durchaus schneller sein. Daher bietet sich ein Wechsel zur gewöhnlichen Multiplikation anstelle eines rekursiven Aufrufs an, sobald die Matrizendimensionen klein genug sind (Cut-Off).
Aufwand
[Bearbeiten | Quelltext bearbeiten]Der Standardalgorithmus zur Matrizenmultiplikation benötigt
Multiplikationen der Elemente des Ringes . Die benötigten Additionen sind hierbei nicht in die Komplexitätsberechnung eingeflossen, Sie können, abhängig von , in Computerimplementationen viel schneller sein als die Multiplikationen. (Insbesondere bei gewöhnlichen ganzen oder Fließkommazahlen ist das oft der Fall.) Mit dem Strassen-Algorithmus wird die Anzahl der Multiplikationen auf
reduziert. Die Reduktion der Anzahl der Multiplikationen führt allerdings zu einer Verringerung der numerischen Stabilität.[1]
Eine saubere Analyse einschließlich der Additionen ist mit dem Master-Theorem möglich: Die gewöhnliche Matrizenmultiplikation benötigt Schritte (Multiplikationen und Additionen gleich gewichtet und zusammenaddiert). Dies gilt auch für den ganz oben erklärten naiven rekursiven Algorithmus, denn er erzeugt 8 Teilprobleme der Größe und zudem sind 4 quadratische Matrizen der Seitenlänge zu addieren, was einen zusätzlichen Aufwand von nach sich zieht, also gilt für seine Laufzeit die Rekursion
was nach dem Master-Theorem nach sich zieht.
Der Strassen-Algorithmus erzeugt hingegen jeweils nur sieben solche Teilprobleme, auch wenn dafür nun 18 Additionen oder Subtraktionen von Matrizen mit halber Seitenlänge, also Additionen/Subtraktionen einzelner Matrixeinträge in , erforderlich sind:
Mit dem Master-Theorem folgt (mit ).
Literatur
[Bearbeiten | Quelltext bearbeiten]- Volker Strassen: Gaussian Elimination is not Optimal. In: Numerische Mathematik, Band 13, 1969, S. 354–356, ISSN 0029-599X, doi:10.1007/BF02165411.
Weblinks
[Bearbeiten | Quelltext bearbeiten]- Eric W. Weisstein: Strassen Formulas. In: MathWorld (englisch).





































