Multiplikation
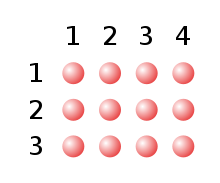
Die Multiplikation (lateinisch multiplicatio, von multiplicare ‚vervielfachen‘, auch Malnehmen genannt) ist eine der vier Grundrechenarten in der Arithmetik. Ihre Umkehroperation ist die Division (das Teilen). Das Rechenzeichen für die Multiplikation ist das Malzeichen „·“ bzw. „ד (sowie „*“).
Namensgebung[Bearbeiten | Quelltext bearbeiten]
Die Multiplikation natürlicher Zahlen und entsteht durch das wiederholte Addieren (Zusammenzählen) des gleichen Summanden:
- .
und nennt man Faktoren, wobei als Multiplikator und als Multiplikand bezeichnet wird. Die Rechnung, gesprochen „ mal “, heißt Multiplikation, das Ergebnis heißt Produkt. Zum Beispiel schreibt man für und spricht diesen Term als „drei mal vier“ oder „dreimal vier“. Anstelle von wird manchmal auch oder geschrieben.
In ihrer Beziehung zum Produkt gelten beide, und , als Teiler (von ), und ist durch beide, wie , teilbar.
Bei der Multiplikation mit Variablen wird der Punkt oft weggelassen, z. B. , . Hierbei ist zu beachten, dass durch die Juxtaposition der Rang der Rechenoperation verändert werden kann, die korrekte Auflösung ist daher , ohne andere Rechenoperationen vereinfacht sich dies wegen des Assoziativgesetzes zu . Vereinfacht gesagt ist ein „Weglassen“ des Malzeichens nur dann erlaubt, wenn das Einfügen von Klammern um Multiplikator und Multiplikand keine Veränderung an der Rechnung verursacht (siehe Rechengesetze unten). Dies ist insbesondere zu beachten, wenn Teilungen (Divisionen) mit in der Gleichung vorkommen, z. B. , da diese nicht assoziativ sind. Zur richtigen Schreibweise siehe Malzeichen.
Bei der Multiplikation mehrerer oder vieler Zahlen kann man das Produktzeichen (abgeleitet vom großen griechischen Pi) verwenden:
sind ganze Zahlen, wird Laufvariable genannt. Im Fall hat man das leere Produkt, welches als definiert ist.
Beispiel 1:
Beispiel 2:
Die unter anderem in der Kombinatorik häufig verwendete Fakultät ist eine besondere Multiplikation natürlicher Zahlen:
Wiederholtes Multiplizieren mit dem gleichen Faktor führt zum Potenzieren, z. B. ist

Die anschauliche Verallgemeinerung der Multiplikation und ihrer Rechenregeln auf die rationalen und reellen Zahlen erreicht man durch Betrachten eines Rechtecks mit den Seitenlängen und (in einer vorgegebenen Längeneinheit). Der Flächeninhalt dieses Rechtecks (in der entsprechenden Flächeneinheit) ist definiert als das Produkt .
Die Multiplikation rationaler Zahlen lässt sich auch formal mit Hilfe von Brüchen definieren. Ebenso kann man die Multiplikation während des Konstruktionsvorganges der reellen aus den rationalen Zahlen definieren.
Die Umkehroperation zur Multiplikation ist die Division, die auch als Multiplikation mit dem Kehrwert aufgefasst werden kann.
Rechengesetze[Bearbeiten | Quelltext bearbeiten]
In einem Körper (also insbesondere , oder ) gelten für alle (siehe Mathematik)
| Assoziativgesetz | |
| Kommutativgesetz | |
| Distributivgesetz | |
| neutrales Element | |
| inverses Element | |
| absorbierendes Element |
Kommutativität[Bearbeiten | Quelltext bearbeiten]
In Anbetracht der so unterschiedlichen Rollen von als Multiplikator (Vervielfacher) einerseits und als Multiplikand (Vervielfachtem) andererseits ist es nicht völlig selbstverständlich, dass die Multiplikation kommutativ ist, d. h. bei Rollentausch dasselbe herauskommt. Durch vollständige Induktion und unter Zuhilfenahme des linken und des rechten Distributivgesetzes sowie der Eigenschaft, dass Links- und Rechtsmultiplikation mit 0 das Resultat 0 ergeben (die selbst wieder durch vollständige Induktion bewiesen werden können), lässt sich die Kommutativität der Multiplikation natürlicher Zahlen beweisen:
- ,
- und aus der Annahme von folgt .
Gaußsche Summenfaktor-Regel[Bearbeiten | Quelltext bearbeiten]
Bei der Multiplikation einer Anzahl beliebiger Faktoren wird dann das größtmögliche Produkt erreicht, wenn bei gleichbleibender Summe der Faktoren die Gesamtdifferenz zwischen den Faktoren möglichst gering ist. Die Gesamtdifferenz errechnet sich, indem man alle Differenzen zwischen den Faktoren addiert.
- Beispiel
Produkt dreier Faktoren. Die Summe der Faktoren ist jeweils 30.
Mit steigender Gesamtdifferenz zwischen den Faktoren wird das Produkt (in der Regel) kleiner.
Gesamtdifferenz 10 · 10 · 10 = 1000 0 ( 0 + 0 + 0 ) 9 · 10 · 11 = 990 4 ( 1 + 2 + 1 ) 8 · 11 · 11 = 968 6 ( 3 + 3 + 0 ) 8 · 10 · 12 = 960 8 ( 2 + 4 + 2 ) 7 · 11 · 12 = 924 10 ( 4 + 5 + 1 ) 7 · 10 · 13 = 910 12 ( 3 + 6 + 3 ) … 0 · 1 · 29 = 0 58 ( 1 + 29 + 28) 0 · 0 · 30 = 0 60 ( 0 + 30 + 30)
Die Gaußsche Summenfaktor-Regel ist äquivalent mit der Aussage, dass der Inhalt einer geometrischen Figur maximal ist, wenn dessen Seiten gleiche Länge haben. So ist das Quadrat bei gleichem Umfang das Rechteck mit dem größten Flächeninhalt.
Weitere Gesetze der Multiplikation[Bearbeiten | Quelltext bearbeiten]
- Bei der Berechnung eines komplexen Terms gilt die Regel Klammer vor Punkt vor Strich.
- Ein Produkt hat den Wert , wenn wenigstens ein Faktor ist, z. B. .
- Multipliziert man eine Zahl mit , so bleibt ihr Wert unverändert . Das gilt sinngemäß auch für die Division.
- Multipliziert man eine Zahl mit sich selbst, erhält man ihre Quadratzahl, z. B. . Multipliziert man eine Zahl zweimal mit sich selbst, erhält man ihre Kubikzahl, z. B. . Manche ganze Zahlen sind zugleich Quadrat- und Kubikzahlen, z. B. .
- Multipliziert man zwei Zahlen mit demselben Vorzeichen, so ist das Produkt positiv. Haben sie unterschiedliche Vorzeichen, so ist das Produkt negativ. Das gilt sinngemäß auch für die Division.
- Multipliziert man eine ungerade Zahl mit einer anderen ungeraden Zahl, so ist das Produkt ebenfalls ungerade. Multipliziert man zwei gerade Zahlen oder eine gerade und eine ungerade Zahl, so ist das Produkt gerade.
- Bei der Multiplikation zweier Brüche werden der Zähler des ersten Bruches mit dem des zweiten Bruches und der Nenner des ersten Bruches mit dem des zweiten Bruches multipliziert. Der Nenner eines Bruches, auch wenn er Variablen enthält, darf nicht ergeben. Das Ergebnis ist gegebenenfalls zu kürzen.
- In Ungleichungen dreht sich das Ungleichheitszeichen um, wenn mit einer negativen Zahl multipliziert (oder durch sie dividiert) wird, z. B.
Algorithmen[Bearbeiten | Quelltext bearbeiten]
Schriftliche Multiplikation[Bearbeiten | Quelltext bearbeiten]
Die schriftliche Multiplikation ist ein Verfahren, um zwei natürliche Zahlen miteinander zu multiplizieren. Die Grundidee ist:
- Die Basis des gewählten Stellenwertsystems bestimmt die Ziffern der Zerlegungen der beiden Faktoren.
- Jede Ziffer des einen Faktors wird mit jeder Ziffer des anderen Faktors malgenommen. Dabei entstehende Überträge werden stellengerecht aufbewahrt.
- All diese Teilergebnisse werden zusammen mit eventuellen Überträgen stellengerecht addiert.
Die Gesamtsumme ergibt das Produkt der beiden Faktoren.
Formaler: Falls die zu multiplizierenden Zahlen und im Stellenwertsystem zur Basis gegeben sind, so lässt sich die Multiplikation unter Zuhilfenahme des Einmaleins wie folgt auf die Addition zurückführen:
Das Einmaleins wird dabei benötigt, um die Produkte zu berechnen.
Diese Methode eignet sich auch zum Multiplizieren rationaler Zahlen mit endlich vielen Nachkommastellen. In diesem Fall treten bei der Darstellung von und im entsprechenden Stellenwertsystem negative Exponenten auf, z. B.: .
Multiplikation mit den Fingern[Bearbeiten | Quelltext bearbeiten]
Nicht nur das Addieren, sondern auch das Multiplizieren lässt sich in begrenztem Umfang mit den Fingern bewerkstelligen. Hierzu müssen beide Faktoren in ein und derselben Dekadenhälfte liegen, also entweder beide auf Ziffern von 1 bis 5 oder auf Ziffern von 6 bis 0 enden.
Im ersten Fall nummeriert man die Finger beginnend beim kleinen Finger mit 10 · (d-1) + 1 bis 10 · (d-1) + 5 für den Daumen durch, wobei d für die Dekade der entsprechenden Zahl steht (also beispielsweise 11 bis 15 für die zweite Dekade). Danach hält man die zwei Finger, deren Produkt man ausrechnen will, aneinander. Das entsprechende Produkt erhält man, indem man die unteren Finger zählt (die beiden aneinandergehaltenen Finger zählen dazu) und mit d · 10 multipliziert, dazu das Produkt der unteren Finger der linken Hand mit den unteren Fingern der rechten Hand (jeweils mit den zusammengehaltenen Fingern) und schließlich eine additive Konstante (d-1)² · 100 addiert.
Im zweiten Fall nummeriert man die Finger von 10 · (d-1) + 6 bis 10 · d durch (also beispielsweise 16 bis 20). Danach hält man analog zum ersten Fall die beiden Finger der gewünschten Faktoren aneinander, zählt die unteren Finger, aber multipliziert diese jetzt mit d · 10 und zählt zu diesem das Produkt der oberen Finger (wieder ohne die zusammengehaltenen Finger) hinzu und die additive Konstante ergibt sich als (d-1) · d · 100.

- Um beispielsweise 7 mal 8 zu rechnen, zählt man die unteren Finger – hier sind es 5 – und multipliziert sie mit 10 (d = 1). Man erhält 50. Nun multipliziert man die oberen Finger der einen Hand – hier 3 – mit der der anderen – hier 2 – und kommt auf 3 · 2 = 6. Jetzt die beiden Zwischenergebnisse addieren, also 50 + 6 = 56, und man erhält das Endergebnis. Die additive Konstante (d-1) · d · 100 ist hier 0 · 1 · 100 = 0.

- Beim Multiplizieren von 24 und 22 zählt man die unteren Finger auf 6, multipliziert dies mit 20 ((d-1) · 10 = 2 · 10) zu 120, addiert dazu das Produkt der unteren Finger 4 · 2 = 8 und die additive Konstante (d-1)² · 100 = 400 und erhält dadurch 528.
Besonders geeignet ist dieses Verfahren für das schnelle Errechnen von Quadratzahlen ohne Taschenrechner. Für Faktoren verschiedener Dekaden und Dekadenhälften kann man dieses Verfahren immer noch anwenden, indem man die Faktoren in Summen aufspaltet.
Hintergrund für dieses Verfahren ist die Tatsache, dass man solche Produkte schreiben kann als:
und Produkte der zweiten Dekadenhälfte errechnen kann, indem man die Komplemente der letzten Ziffer bzgl. 10 bildet. Die letzte Ziffer ist dann das Produkt der Komplemente, die Zehner das Komplement der Summe der Komplemente.
Vedische Multiplikation[Bearbeiten | Quelltext bearbeiten]
Diese Rechenart kommt aus Indien und ist ein Teil der sogenannten vedischen Mathematik. Bei diesem Rechensystem werden zuerst die Zahlen analysiert und danach ein passendes Verfahren zu deren Berechnung ausgewählt. So existiert z. B. ein Verfahren, welches sich immer dann zu einer „Blitz“-Multiplikation auch großer Faktoren eignet, wenn diese knapp unter oder über derselben Zehnerpotenz liegen.
Dem Rechenweg liegt folgende Beziehung zugrunde: und seien zwei Zahlen dicht bei einer Zehnerpotenz und bzw. die Differenzen hierzu. Dann ist
Falls nun ist, kann man die beiden Ziffernfolgen von und einfach nebeneinander schreiben, um so zur Lösung der Multiplikation zu gelangen. (Achtung: Führende Nullen des zweiten Terms müssen mitgeschrieben werden.)
- Beispiele
95 ∙ 97 = 9215 992 ∙ 988 = 980096 12 ∙ 13 = 156 98 ∙ 102 = 9996
Fakt. Diff. Fakt. Diff. Fakt. Diff. Fakt. Diff.
a, b zu 100 a, b zu 1000 a, b zu 10 a, b zu 100
––––––––––––––– –––––––––––––––– –––––––––––––– ––––––––––––––-
95 -5 992 -8 12 +2 98 -2
\ ∙ \ ∙ \ ∙ \ ∙
97 -3 988 -12 13 +3 102 +2
––––––––––––––– –––––––––––––––– –––––––––––––– ––––––––––––––-
92 15 980 096 15 6 99 96
(95-3) (-5∙-3) (992-12) (-8∙-12) (12+3) (3∙2) (98+2-1) (100+(-2)∙2) (97-5) (5∙3) (988- 8) (8∙12) (13+2) (3∙2) (102-2-1) (100-2∙2)
Im letzten Fall liegt eine Zahl über und eine unter 100. Da in diesem Fall das Produkt ist, muss von der linken Zahl noch ein Übertrag besorgt werden, also links , rechts .
Natürlich ergibt eine Vertauschung der Faktoren dasselbe Ergebnis, da ist, siehe dazu die letzte Zeile des Beispiels. Da gleiche Vorzeichen beim Multiplizieren von zwei Zahlen immer zu + werden, kann man sie für diese Fälle auch weglassen, wie in der letzten Zeile angegeben.
Als Basis können außerdem noch und verwendet werden. Berechnet wird hier wie bei , nur wird rechts bzw. als Differenz gebildet und links mit 2 multipliziert (Basis 20) bzw. durch 2 dividiert (Basis 50). Für die Basis 50 wird im Fall, dass die linke Summe ungerade ist, nur der ganzzahlige Anteil nach Division durch 2 verwendet und als Übertrag rechts addiert; Beweis entsprechend zu durch Einsetzen und Umformen.
Russische Bauernmultiplikation[Bearbeiten | Quelltext bearbeiten]
A und B seien ganzzahlige Faktoren. Das Produkt P = A · B kann auch auf folgende – scheinbar kuriose – Art ermittelt werden:
- Schritt: Dividiere A und die Ergebnisse so lange durch 2, bis sich 1 als Ergebnis einstellt. Dabei wird ein nicht ganzzahliges Ergebnis auf die nächste ganze Zahl abgerundet und danach die Division durch 2 fortgesetzt.
- Schritt: Verdopple B fortlaufend.
- Schritt: Streiche alle Verdoppelungen in Spalte B, bei denen in Spalte A die Halbierung eine gerade Zahl ist.
- Schritt: Addiere alle nicht gestrichenen Zahlen der Spalte B. Die erhaltene Summe ist das gesuchte Produkt P.
Beispiel: 11 · 3 = ?
Spalte A Spalte B
11 · 3
5 6
2 12 gestrichen, wegen der geraden Zahl 2 in Spalte A
1 24
_______________________
Summe 33
Erklärung[Bearbeiten | Quelltext bearbeiten]
In der Spalte A werden Streichungen vorgenommen, wo bei der dezimalen Zahl 11 in der binären Darstellung Nullen stehen: 11 (dezimal) = 1011 (binär). Dabei ist die Spalte A von unten nach oben zu lesen. Diese Methode ist auch die einfachste Art, dezimale Zahlen in binäre zu transformieren. Die fortlaufenden Verdoppelungen in der Spalte B entsprechen den Zweierpotenzen des binären Zahlensystems, multipliziert mit dem zweiten Faktor. Wo in Spalte A eine Null steht, wird die entsprechende Zahl in B mit 0 multipliziert, daher gestrichen. Alle übrigen Zahlen der Spalte B gehören zum Produkt und werden summiert.
Man kann dies auch leicht anders formulieren.
Die letzte Gleichung kommt der binären Darstellung 1011 von 11 gleich.
Duplation[Bearbeiten | Quelltext bearbeiten]
Die Duplation (von lateinisch duplare ‚verdoppeln‘) ist eine Multiplikationsmethode, bei der zunächst tabellarisch links zeilenweise ganzzahlige Vielfache des ersten Faktors F1 (einschließlich des Ein-Fachen, also des Faktors selbst) und rechts daneben in die jeweilige Zeile die Vielfachheit aufgeschrieben werden. Standardmäßig werden die jeweils darüber stehenden Werte verdoppelt (daher der Name Duplation), also der Reihe nach das 1-, 2-, 4-, 8-, 16-fache usw. notiert, bis mit der Zahl der Vielfachheit der zweite Faktor erreicht ist. Anschließend wird der zweite Faktor additiv in Summanden aus den notierten Vielfachheiten zerlegt und der Produktwert ermittelt, indem die zugehörigen Vielfachen des ersten Faktors addiert werden.
Der zweite Faktor F2 lässt sich stets „kanonisch“ und somit eindeutig in seine Binärdarstellung als Summe von Zweierpotenzen zerlegen, womit die Verdoppelung immer zum Ziel führt. Indes ist die Verwendung von Zweierpotenzvielfachen aber nicht zwingend erforderlich. Man kann F2 nämlich durchaus auch in andere Summanden zerlegen, z. B. Zehnerpotenzen, die sich u. U. einfacher als durch fortgesetzte Verdoppelung berechnen lassen. Wenn der zweite Faktor z. B. „1105“ ist, dann wäre es zwar machbar, aber unökonomisch, bis zum 512-fachen zu verdoppeln. Man kann sich vielmehr auf die Verdoppelungsschritte 2-fach und 4-fach beschränken und dazu die einfach zu berechnenden 100- und 1000-fachen des ersten Faktors nehmen und damit F2 als 1000+100+4+1=1105 darstellen. Das Finden einer geschickten Zerlegung des zweiten Faktors ist Sache der Intuition und Erfahrung des Rechners.
Zu Ende gedacht (aber unbelegt) wäre es ausreichend, nur das 2-, 4- und 8-fache des ersten Faktors durch Duplikation zu berechnen und daraus je nach Bedarf durch – ggf. mehrfache – Verzehnfachung die erforderlichen größeren Summanden zu ermitteln.
Multiplikation mit Zirkel und Lineal[Bearbeiten | Quelltext bearbeiten]
Für eine graphische Multiplikation mit Zirkel und Lineal kann man den Sehnensatz (Bild 1) verwenden: Durch einen Punkt O zeichnet man eine Gerade und trägt von O aus, die zu multiplizierenden Längen und in entgegengesetzten Richtungen ab. Dadurch entstehen zwei neue Punkte A und B. Durch O zeichnet man eine zweite Gerade. Auf dieser trägt man eine Strecke der Länge 1 ab, wodurch ein weiterer Punkt E entsteht. Die zweite Gerade wird durch den Kreis durch die Punkte A, B und E in einem Punkt C geschnitten. Der Abstand von O bis C entspricht nach dem Sehnensatz der gesuchten Länge
Den benötigten Kreis kann man als Umkreis um das von A, B und E aufgespannte Dreieck konstruieren.
Neben dem Sehnensatz ist auch der Sekantensatz (Bild 2) für die Konstruktion des Produkts zweier Zahlen dienlich. Bei Verwendung des Sekantensatzes liegt der Startpunkt O außerhalb des Kreises und die Größen a und b werden ausgehend von O in die gleiche Richtung abgetragen. Auf der darauf folgenden Halbgeraden, ab O mit beliebigem Winkel α zu BO, wird C im Abstand 1 zu O festgelegt. Nun bestimmt man den Mittelpunkt des Kreises mithilfe einer Mittelsenkrechten auf AB und AC. Der abschließende Kreis durch C, A und B schneidet die Halbgerade in D. Der Abstand von O bis D entspricht nach dem Sekantensatz der gesuchten Länge
Eine weitere Möglichkeit zur graphischen Multiplikation mit Zirkel und Lineal ergibt sich – so wie bei der Division und der Potenz – aus dem Strahlensatz (Bild 3). Hier trägt man zunächst auf einem Strahl mit Ausgangspunkt A Strecken der Längen 1 und b, die beide in A beginnen. Dann trägt man vom Endpunkt E der Strecke der Länge 1 eine Strecke der Länge a ab und zeichnet einen zweiten Strahl durch deren Endpunkt C und A, so dass A wiederum der Ausgangspunkts des Strahls ist. Dann zeichnet man durch den Endpunkt B der Strecke b eine zu a parallele Gerade. Diese schneidet den zweiten Strahl in D. Die Länge der Strecke BD entspricht dem Produkt von a und b.
Effiziente Algorithmen[Bearbeiten | Quelltext bearbeiten]
Sei . Um zwei natürliche Zahlen der Länge zu multiplizieren, benötigt die schriftliche Multiplikation asymptotische Laufzeit . Lange Zeit war kein effizienterer Algorithmus bekannt, bis Anatoli Alexejewitsch Karazuba 1960 den nach ihm benannten Karazuba-Algorithmus entdeckte.[1] In den Folgejahren wurden Algorithmen mit immer besserer Zeitkomplexität gefunden, bis schließlich 2019 Harvey und van der Hoeven einen Algorithmus mit Laufzeit veröffentlichten. Von diesem wird vermutet, dass er asymptotisch optimal ist, d. h. dass es keinen Multiplikationsalgorithmus mit besserer Zeitkomplexität gibt -- was allerdings noch unbewiesen ist. Nachfolgende Tabelle gibt eine Übersicht über verschiedene bekannte Algorithmen.
| Algorithmus | Entdeckungsjahr | Zeitkomplexität |
|---|---|---|
| Schriftliche Multiplikation | - | |
| Karazuba-Algorithmus | 1960 | |
| Toom-Cook-Algorithmus | 1966 | wobei eine beliebige Konstante ist |
| Schönhage-Strassen-Algorithmus | 1971 | |
| Fürers Algorithmus | 2007 | wobei den iterierten Logarithmus bezeichnet |
| Harvey & van-der-Hoeven-Algorithmus[2] | 2019 |
Zurückführen der Multiplikation rationaler Zahlen auf die natürlicher Zahlen[Bearbeiten | Quelltext bearbeiten]
Jeder Algorithmus, der zwei natürliche Zahlen multipliziert, kann auch verwendet werden, um zwei ganze bzw. rationale Zahlen zu multiplizieren.
Um ganze Zahlen zu multiplizieren, verwendet man die Formel
wobei die Vorzeichenfunktion bezeichnet und die Betragsfunktion.
Zur Multiplikation zweier rationaler Zahlen (mit ), verwendet man
Mehr oder weniger als zwei Faktoren[Bearbeiten | Quelltext bearbeiten]
Das Produkt von mehr als zwei Faktoren wird so definiert, dass man von links beginnend je zwei Faktoren multipliziert und so fortfährt, bis nur eine Zahl übrigbleibt. Das Assoziativgesetz besagt nun, dass man an beliebiger Stelle beginnen kann, also auch von rechts. Aufgrund des Kommutativgesetzes ist auch die Reihenfolge irrelevant, so dass mit zwei beliebigen Faktoren (welche also nicht direkt beieinanderstehen müssen) angefangen werden kann.
Auch das Produkt von einem einzigen oder von gar keinen Faktoren ist definiert, obwohl man dazu nicht mehr multiplizieren muss: Das Produkt einer Zahl ist diese Zahl selbst, und das Produkt von keinem Faktor ist 1 (allgemein das neutrale Element der Multiplikation). Letzteres wird auch Leeres Produkt genannt.
Es ist auch möglich, ein unendliches Produkt zu bilden. Dabei spielt die Reihenfolge der Faktoren allerdings eine Rolle, man kann die Faktoren also nicht mehr beliebig vertauschen, und auch beliebige Zusammenfassungen zu Teilprodukten sind nicht immer möglich (ähnlich wie bei unendlichen Summen).
Verallgemeinerungen[Bearbeiten | Quelltext bearbeiten]
Die bekannte Multiplikation reeller Zahlen kann zur Multiplikation komplexer Zahlen der Form verallgemeinert werden durch Nutzung des Distributivgesetzes:
Durch Forderung einiger der oben angegebenen Rechengesetze gelangt man zu algebraischen Strukturen mit zwei Verknüpfungen, einer Addition und einer Multiplikation. In einem Ring gibt es eine Addition, mit der die Menge eine Abelsche Gruppe bildet, und eine Multiplikation, die assoziativ und distributiv ist. Hat die Multiplikation ein neutrales Element, nennt man den Ring unitär. Ist zusätzlich die Division immer möglich, erhält man einen Schiefkörper. Ist zusätzlich die Multiplikation kommutativ, erhält man einen Körper.
Mit dieser Multiplikation nicht zu verwechseln sind andere Verknüpfungen, die gemeinhin auch als Produkte bezeichnet werden, z. B. das Skalarprodukt in euklidischen Vektorräumen, die Skalarmultiplikation in Vektorräumen, die Matrizenmultiplikation und das Kreuzprodukt im dreidimensionalen Raum . Von Multiplikation spricht man auch bei Größenwerten von physikalischen Größen.
Siehe auch[Bearbeiten | Quelltext bearbeiten]
- Linearfaktor, Primfaktorzerlegung
- Effiziente Multiplikationsalgorithmen: Schönhage-Strassen-Algorithmus, Karatsuba-Algorithmus, Toom-Cook-Algorithmus
- Plutimikation, Pippi Langstrumpfs Art zu rechnen
Weblinks[Bearbeiten | Quelltext bearbeiten]
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Proceedings of the Steklov Institute of Mathematics, Vol. 211, 1995, pp. 169–183. Translated from Trudy Matematicheskogo Instituta imeni V.A. Steklova, Vol. 211, 1995, pp. 186–202.
- ↑ David Harvey, Joris van der Hoeven: Integer multiplication in time O(n log n). Annals of Mathematics, Princeton University, Department of Mathematics, In press. hal-02070778v2


































































































