Vorrangwarteschlange
In der Informatik ist eine Vorrangwarteschlange (auch Prioritätenliste, Prioritätsschlange, Prioritätswarteschlange oder englisch priority queue genannt) eine spezielle abstrakte Datenstruktur, genauer eine erweiterte Form einer Warteschlange. Den Elementen, die in die Warteschlange gelegt werden, wird ein Schlüssel mitgegeben, der die Reihenfolge der Abarbeitung der Elemente bestimmt.
Operationen[Bearbeiten | Quelltext bearbeiten]
Vorrangwarteschlangen müssen die folgenden Operationen unterstützen:
- insert – Einfügen eines Elements
- extractMin – Rückgabe und Entfernen des Elements mit dem kleinsten Schlüssel (= höchste Priorität)
- isEmpty – Überprüfen, ob die Warteschlange leer ist
Daneben gibt es noch Operationen, die vor allem für Online-Algorithmen wichtig sind:
- remove – Entfernen eines Elements
- decreaseKey – den Schlüsselwert verringern (d. h. die Priorität erhöhen)
Weitere häufig verwendete Operationen sind:
- peek – Zurückgeben des Elements mit der höchsten Priorität, ohne die Warteschlange zu verändern
- merge – Zusammenfügen von zwei Vorrangwarteschlangen
Implementierung[Bearbeiten | Quelltext bearbeiten]
Die Implementierung von Vorrangwarteschlangen kann über AVL-Bäume erfolgen. Sowohl insert als auch extractMin können dann in O(log n) Zeit ausgeführt werden. Eine andere Möglichkeit besteht in der Verwendung partiell geordneter Bäume (Heaps). Auch hier liegt die Zeitkomplexität bei O(log n).
Beispiele für Datenstrukturen, die Vorrangwarteschlangen effizient implementieren, sind
- AVL-Baum
- Binärer Heap
- Binomial-Heap
- Fibonacci-Heap (amortisierte Laufzeit für remove und extractMin: O(log n), ansonsten O(1), im schlechtesten Fall O(n) bzw. O(log n))
- K-Level Buckets
- Linksbaum
- Radix-Heap
- Van-Emde-Boas-Vorrangwarteschlange
Die folgende Tabelle zeigt eine Übersicht über die verschiedenen Laufzeiten von einigen Implementierungen in O-Notation.
| Operation | peek | extractMin | insert | decreaseKey | merge |
|---|---|---|---|---|---|
| Binärer Heap[1] | Θ(1) | Θ(log n) | O(log n) | O(log n) | Θ(n) |
| Linksbaum[2] | Θ(1) | Θ(log n) | Θ(log n) | O(log n) | Θ(log n) |
| Binomial-Heap[1][3] | Θ(1) | Θ(log n) | Θ(1)a | Θ(log n) | O(log n)b |
| Fibonacci-Heap[1][4] | Θ(1) | O(log n)a | Θ(1) | Θ(1)a | Θ(1) |
Anwendungen[Bearbeiten | Quelltext bearbeiten]
Prioritätswarteschlangen können für die Implementierung diskreter Ereignissimulationen genutzt werden. Dabei werden zu den jeweiligen Ereignissen als Schlüssel die Zeiten berechnet, das Zeit-Ereignis-Paar in die Vorrangwarteschlange eingefügt, und die Vorrangwarteschlange gibt dann das jeweils aktuelle (d. h. als Nächstes zu verarbeitende) Ereignis aus.
Allgemein werden Vorrangwarteschlangen für viele Algorithmen oder sogar Klassen von Algorithmen benötigt.
Zum Beispiel machen Gierige Algorithmen von Prioritätswarteschlangen Gebrauch, da dort häufig das Minimum oder Maximum einer Menge bestimmt werden muss. Einer der bekanntesten Algorithmen dieser Art ist der Algorithmus von Dijkstra zur Berechnung kürzester Wege.
Ebenso kann man Vorrangwarteschlangen für Bestensuche-Algorithmen verwenden. Um in einer Iteration den nächsten vielversprechendsten Knoten zu finden, wird meist eine Vorrangwarteschlange benutzt. Ein Beispiel hierfür ist der A*-Algorithmus, um kürzeste Wege in Graphen zu berechnen.
Ein spezieller Algorithmus, der auch mit Vorrangwarteschlangen implementiert werden kann, ist die Huffman-Kodierung. Die Vorrangwarteschlange wird hierbei dafür verwendet, die Zeichen mit der kleinsten Wahrscheinlichkeit zu finden.
Erweiterungen[Bearbeiten | Quelltext bearbeiten]
Neben der klassischen, einendigen Vorrangwarteschlange existieren auch zweiendige. Diese unterstützen zusätzlich eine Operation extractMax, um das Element mit dem größten Schlüssel herauszuziehen. Eine Möglichkeit für die Implementierung solcher Datenstrukturen bieten Doppelheaps. Alternativ können auch Datenstrukturen wie Min-Max-Heaps genutzt werden, die direkt zweiendige Prioritätswarteschlangen unterstützen.
Parallele Vorrangwarteschlange[Bearbeiten | Quelltext bearbeiten]
Um Vorrangwarteschlangen weiter zu beschleunigen, kann man sie parallelisieren. Dabei gibt es drei verschiedene Möglichkeiten zur Parallelisierung. Die erste Möglichkeit ist es, einfach die einzelnen Operationen (insert, extractMin …) zu parallelisieren. Die zweite Möglichkeit erlaubt den gleichzeitigen Zugriff von mehreren Prozessen auf die Vorrangwarteschlange. Die letzte Möglichkeit ist es, jede Operation auf k Elementen auszuführen, anstatt immer nur auf einem Element. Im Falle von extractMin beispielsweise würde man die ersten k Elemente mit der höchsten Priorität aus der Vorrangwarteschlange herausnehmen.
Einzelne Operationen parallelisieren[Bearbeiten | Quelltext bearbeiten]
Ein einfacher Ansatz um Vorrangwarteschlangen zu parallelisieren ist, die einzelnen Operationen zu parallelisieren. Das heißt, die Warteschlange funktioniert genau so wie eine sequentielle, allerdings werden die einzelnen Operationen durch den Einsatz von mehreren Prozessoren beschleunigt. Der maximale Speedup, der hierbei erreicht werden kann, ist durch beschränkt, da es sequentielle Implementierungen für Vorrangwarteschlangen gibt, deren langsamste Operation in Zeit läuft (z. B. Binomial-Heap).
Auf einem „Concurrent Read, Exclusive Write“-PRAM-Modell (CREW), können die Operationen insert, extractMin, decreaseKey und remove in konstanter Zeit durchgeführt werden, wenn Prozessoren zur Verfügung stehen, wobei die Größe der Vorrangwarteschlange ist.[5] Die Warteschlange ist im Folgenden als Binomial-Heap implementiert. Dabei muss nach jeder Operation gelten, dass maximal drei Bäume derselben Ordnung existieren und dass die kleinste Wurzel der Bäume von Ordnung kleiner als alle Wurzeln von Bäumen höherer Ordnung ist.
- insert(e): Ein neuer Binomialbaum mit Ordnung 0, dessen einziger Knoten das Element e enthält, wird eingefügt. Danach werden zwei Bäume derselben Ordnung zu einem Baum der Ordnung zusammengefügt, wenn drei Bäume der Ordnung existieren. Der Baum mit der kleinsten Wurzel der Bäume mit Ordnung wird dafür nicht verwendet. Dieser Schritt wird parallel ausgeführt, indem sich jeder Prozessor um die Bäume einer Ordnung kümmert. Somit ist insert in durchführbar.
Nachfolgend ist die Operation in Pseudocode aufgeführt.
insert(e) {
L[0] = L[0] ∪ e
parallelesZusammenfügen()
}
parallelesZusammenfügen() {
für jede Ordnung i parallel:
falls |L[i]| >= 3:
füge zwei Bäume aus L[i] \ min(L[i]) zu einem neuen Baum b zusammen
L[i+1] = L[i+1] ∪ b
}
- extractMin: Das zu entfernende Minimum ist das kleinste Element der Bäume von Ordnung 0. Dieses Element wird entfernt. Um sicherzustellen, dass sich das neue Minimum danach auch in Ordnung 0 befindet, wird für jede Ordnung der Baum mit der kleinsten Wurzel aufgeteilt und die zwei neuen Bäume der Ordnung hinzugefügt. Indem jeder Prozessor genau einer Ordnung zugewiesen wird, kann dieser Schritt parallel in ausgeführt werden. Nach diesem Schritt werden wie bei der insert-Operation zwei Bäume der Ordnung zu einem Baum der Ordnung zusammengefügt, wenn mindestens drei Bäume der Ordnung existieren. Da dieser Schritt auch für jede Ordnung parallel ausgeführt werden kann, ist extractMin in konstanter Zeit ausführbar.
extractMin() {
e = min(L[0])
L[0] = L[0]\e
für jede Ordnung i parallel:
falls |L[i]| >= 1:
teile min(L[i]) in zwei Bäume a,b
L[i] = L[i] \ min(L[i])
L[i-1] = L[i-1] ∪ {a,b}
parallelesZusammenfügen()
return e
}
Das Konzept für konstante Insert- und ExtractMin-Operationen kann erweitert werden, um auch eine konstante Laufzeit für remove zu erreichen. Die DecreaseKey-Operation kann dann durch ein Remove und ein darauffolgendes Insert ebenso in konstanter Zeit realisiert werden.[5]
Der Vorteil dieser Parallelisierung ist, dass sie genau so wie eine normale, sequentielle Vorrangwarteschlange angewendet werden kann. Aber es kann auch nur ein Speedup von erreicht werden. Dieser wird in der Praxis noch weiter dadurch beschränkt, dass bei einer parallelen Implementierung zusätzlicher Aufwand für die Kommunikation zwischen den verschiedenen Prozessoren betrieben werden muss.
Gleichzeitiger paralleler Zugriff[Bearbeiten | Quelltext bearbeiten]
Falls der gleichzeitige Zugriff auf eine Vorrangwarteschlange erlaubt ist, können mehrere Prozesse gleichzeitig Operationen auf die Vorrangwarteschlange anwenden. Dies wirft jedoch zwei Probleme auf. Zum einen ist die Semantik der einzelnen Operationen nicht mehr offensichtlich. Zum Beispiel, wenn zwei Prozesse gleichzeitig extractMin ausführen, sollten beide Prozesse das gleiche Element erhalten oder unterschiedliche? Dies schränkt die Parallelität auf die Ebene der Anwendung ein, welche die Vorrangwarteschlange benutzt. Zum anderen gibt es das Problem des Zugriffskonfliktes, da mehrere Prozesse Zugriff auf das gleiche Element haben.
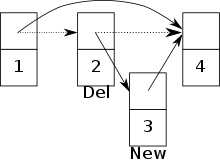
Auf einem „Concurrent Read, Concurrent Write“-PRAM-Modell (CRCW) kann der gleichzeitige Zugriff auf eine Vorrangwarteschlange implementiert werden. Im Folgenden ist die Vorrangwarteschlange als Skip-Liste implementiert.[6][7] Zusätzlich wird eine atomare Synchronisationsprimitive CAS benutzt, um eine Lock-freie Skip-Liste zu ermöglichen. Die Knoten der Skip-Liste bestehen aus einem einzigartigen Schlüssel, einer Priorität, einem Array aus Zeigern auf die nächsten Knoten und aus einem Delete-Kennzeichen. Das Delete-Kennzeichen gibt an, ob der Knoten gerade dabei ist, von einem Prozess gelöscht zu werden. Dadurch wissen die anderen Prozesse, dass der Knoten kurz davor ist gelöscht zu werden und können, je nachdem, welche Operationen sie ausführen, entsprechend darauf reagieren.
- insert(e): Zuerst wird ein neuer Knoten mit einem Schlüssel und einer Priorität erstellt. Zusätzlich wird dem Knoten noch eine Anzahl an Level übergeben. Dann wird eine Suche gestartet, um die richtige Position in der Skip-Liste zu finden, wo man den neu erstellten Knoten hinzufügen muss. Die Suche startet vom ersten Knoten und vom höchsten Level aus und traversiert die Skip-Liste herunter bis zum niedrigsten Level, bis die korrekte Position gefunden wurde. Dabei wird für jedes Level der zuletzt traversierte Knoten als Vorgängerknoten gespeichert. Zusätzlich wird jener Knoten, zu dem der Zeiger des Vorgängerknoten zeigt, als Nachfolgerknoten gespeichert. Danach wird für jedes Level des neuen Knotens der Zeiger des gespeicherten Vorgängerknotens auf den neuen Knoten gesetzt. Schlussendlich werden noch die Zeiger, für jedes Level, des neuen Knotens auf die entsprechenden Nachfolgerknoten gesetzt.
- extractMin(): Zuerst wird die Skip-Liste traversiert, bis ein Knoten erreicht wird, dessen Delete-Kennzeichen nicht gesetzt ist. Dann wird das Delete-Kennzeichen für diesen Knoten gesetzt. Abschließend werden die Zeiger des Vorgängerknotens aktualisiert.
Beim Erlauben vom gleichzeitigen Zugriff auf eine Vorrangwarteschlange muss darauf geachtet werden, dass es zu möglichen Konflikten zwischen zwei Prozessen kommen kann. Zum Beispiel kann es zu einem Konflikt kommen, falls ein Prozess versucht, einen Knoten hinzuzufügen, aber ein anderer Prozess schon dabei ist, seinen Vorgängerknoten zu löschen.[6] Die Gefahr besteht, dass der neue Knoten zwar zur Skip-Liste hinzugefügt wurde, aber nun nicht mehr erreichbar ist. (Siehe Bild)
K-Element-Operationen[Bearbeiten | Quelltext bearbeiten]
Bei dieser Art der Parallelisierung von Vorrangwarteschlangen werden neue Operationen eingeführt, die nicht mehr ein einzelnes Element bearbeiten, sondern Elemente gleichzeitig. Die neue Operation k_extractMin löscht dann die kleinsten Elemente aus der Vorrangwarteschlange und gibt sie zurück. Dabei ist die Warteschlange auf verteiltem Speicher parallelisiert. Jeder Prozessor hat seinen eigenen privaten Speicher und eine lokale (sequentielle) Vorrangwarteschlange. Die Elemente der globalen Warteschlange sind also auf alle Prozessoren verteilt. Bei einer k_insert-Operation werden die Elemente zufällig gleichverteilt den Prozessoren zugewiesen und jeweils in die lokalen Vorrangwarteschlangen eingefügt. Nach wie vor können auch einzelne Elemente eingefügt werden. Mit dieser Strategie gilt mit hoher Wahrscheinlichkeit, dass die global kleinsten Elemente in der Vereinigung der lokal kleinsten Elemente aller Prozessoren sind.[8] Jeder Prozessor hält also einen repräsentativen Teil der globalen Vorrangwarteschlange.
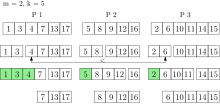
Diese Eigenschaft wird bei k_extractMin ausgenutzt, indem aus jeder lokalen Warteschlange die kleinsten Elemente entfernt werden und in einer Ergebnismenge gesammelt. Dabei bleiben die Elemente aber noch ihrem ursprünglichen Prozessor zugeteilt. Die Anzahl der Elemente, die aus jeder lokalen Vorrangwarteschlange gelöscht werden, ist dabei abhängig von und der Anzahl der Prozessoren .[8] Durch parallele Selektion werden die kleinsten Elemente der Ergebnismenge bestimmt. Mit hoher Wahrscheinlichkeit sind diese auch global die kleinsten Elemente. Falls nicht, werden erneut Elemente aus jeder lokalen Vorrangwarteschlange gelöscht, bis die global kleinsten Elemente in der Ergebnismenge sind. Jetzt können die kleinsten Elemente zurückgegeben werden. Alle anderen Elemente werden wieder in die lokalen Vorrangwarteschlangen eingefügt, aus denen sie entfernt wurden. Die Laufzeit von k_extractMin ist erwartet , wenn und die Größe der Vorrangwarteschlange beschreibt.[8]
Die Vorrangwarteschlange kann noch verbessert werden, indem die Ergebnismenge nach einer k_extractMin-Operation nicht immer direkt wieder in die lokale Warteschlange eingefügt wird. Dadurch erspart man sich, dass Elemente immer wieder aus einer lokalen Warteschlange entfernt und direkt danach wieder eingefügt werden.
Durch das Entfernen von mehreren Elementen gleichzeitig kann gegenüber sequentiellen Vorrangwarteschlangen eine deutliche Beschleunigung erreicht werden. Allerdings können nicht alle Algorithmen diese Art von Vorrangwarteschlange nutzen. Zum Beispiel können beim Dijkstra-Algorithmus nicht mehrere Knoten auf einmal bearbeitet werden. Dijkstra nimmt den Knoten mit der kleinsten Distanz zum Startknoten aus der Vorrangwarteschlange und relaxiert dann dessen Kanten. Dadurch kann sich die Priorität der Nachbarknoten, die sich schon in der Vorrangwarteschlange befinden, verändern. Durch das Herausnehmen der Knoten mit der kleinsten Distanz kann es passieren, dass sich durch die Bearbeitung eines der Knoten die Priorität eines der anderen Knoten ändert. Dieser Knoten sollte dann erst später bearbeitet werden, wird nun aber schon früher bearbeitet. Dadurch wird dieser Knoten dann zu früh als besucht gekennzeichnet. In dem Fall hat man zwar einen Weg vom Startknoten zu diesem Knoten gefunden, aber die Distanz ist nicht minimal. Anders gesagt, wird durch das Verwenden von k-Element-Operationen für den Algorithmus von Dijkstra die Label-Setting-Eigenschaft zerstört.
Siehe auch[Bearbeiten | Quelltext bearbeiten]
Literatur[Bearbeiten | Quelltext bearbeiten]
- George F. Luger: Künstliche Intelligenz. Strategien zur Lösung komplexer Probleme. Pearson Studium, 2001, ISBN 3-8273-7002-7.
Weblinks[Bearbeiten | Quelltext bearbeiten]
java.util.PriorityQueuein der Java API bei Oracle (englisch)
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ a b c Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest: Introduction to Algorithms. In: MIT Press and McGraw-Hill. 1990, ISBN 0-262-03141-8.
- ↑ Clark A. Clane: Linear Lists and Priority Queues as Balanced Binary Trees (Ph.D. thesis). Hrsg.: Department of Computer Science, Stanford University. 1972, ISBN 0-8240-4407-X (stanford.edu).
- ↑ Binomial Heap | Brilliant Math & Science Wiki. brilliant.org, abgerufen am 30. September 2019 (amerikanisches Englisch).
- ↑ Michael Fredman, Robert Tarjan: Fibonacci heaps and their uses in improved network optimization algorithms. In: Journal of the Association for Computing Machinery. Band 34, Nr. 3, Juli 1987, S. 596–615, doi:10.1145/28869.28874 (ict.ac.cn [PDF]). Fibonacci heaps and their uses in improved network optimization algorithms ( des vom 12. Juli 2019 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.
- ↑ a b Gerth Brodal: Priority Queues on Parallel Machines. In: Algorithm Theory - SWAT 96. Springer-Verlag, 1996, S. 416–427, doi:10.1007/3-540-61422-2_150.
- ↑ a b Håkan Sundell, Philippas Tsigas: Fast and lock-free concurrent priority queues for multi-thread systems. In: Journal of Parallel and Distributed Computing. Band 65, Nr. 5, 2005, S. 609–627, doi:10.1109/IPDPS.2003.1213189.
- ↑ Jonsson Lindén: A Skiplist-Based Concurrent Priority Queue with Minimal Memory Contention. In: Technical Report 2018-003. 2013 (uu.se).
- ↑ a b c Peter Sanders, Kurt Mehlhorn, Martin Dietzfelbinger, Roman Dementiev: Sequential and Parallel Algorithms and Data Structures - The Basic Toolbox. Springer International Publishing, 2019, S. 226–229, doi:10.1007/978-3-030-25209-0.











