Huffman-Kodierung
Die Huffman-Kodierung ist eine Form der Entropiekodierung, die 1952 von David A. Huffman entwickelt und in der Abhandlung A Method for the Construction of Minimum-Redundancy Codes publiziert wurde.[1] Sie ordnet einer festen Anzahl an Quellsymbolen jeweils Codewörter mit variabler Länge zu. In der Informationstechnik ist sie ein Präfixcode, der üblicherweise für verlustfreie Kompression benutzt wird. Wie bei anderen Entropiekodierungen werden häufiger vorkommende Zeichen mit weniger Bits repräsentiert als seltener vorkommende Zeichen.
Grundlagen[Bearbeiten | Quelltext bearbeiten]
Um Daten möglichst redundanzfrei darzustellen, müssen die Quellsymbole mit Codewörtern unterschiedlicher Wortlängen kodiert werden. Die Länge der Codewörter entspricht dabei idealerweise ihrem Informationsgehalt. Um einen Code auch wieder eindeutig dekodieren zu können, muss er die Kraftsche Ungleichung erfüllen und zusätzlich noch präfixfrei sein, d. h., kein Codewort darf der Beginn eines anderen sein.
Die Grundidee ist, einen k-nären Wurzelbaum (ein Baum mit jeweils k Kindern je Knoten) für die Darstellung des Codes zu verwenden. In diesem sog. Huffman-Baum stehen die Blätter für die zu kodierenden Zeichen, während der Pfad von der Wurzel zum Blatt das Codesymbol bestimmt. Im Gegensatz zur Shannon-Fano-Kodierung wird der Baum dabei von den Blättern zur Wurzel (englisch bottom-up) erstellt.
Dieser Baum kann mit einem Heap und einer Vorrangwarteschlange implementiert werden.[2][3]
Im Unterschied zum Morsecode benötigt man bei einer Huffman-Codierung keine Trennzeichen. Eine Trennung der Codewörter ist nicht notwendig, da die Codierung präfixfrei ist. Dadurch ist kein Codewort Anfang eines anderen Codewortes.
Der bei der Huffman-Kodierung gewonnene Baum liefert garantiert eine optimale und präfixfreie Kodierung. D. h., es existiert kein symbolbezogenes Kodierverfahren, das einen kürzeren Code generieren könnte, wenn die Auftrittswahrscheinlichkeiten der Symbole bekannt sind.
Geschichte[Bearbeiten | Quelltext bearbeiten]
Im Jahre 1951 hatten David A. Huffman und seine Klassenkameraden am MIT im Kurs Informationstheorie die Wahl zwischen einer Seminararbeit und einer Abschlussprüfung. Die Seminararbeit, betreut von Professor Robert M. Fano, sollte die Findung des effizientesten binären Codes thematisieren. Huffman, der nicht in der Lage war, die Effizienz eines Codes zu beweisen, war nur knapp vor dem Entschluss, aufzugeben und sich für die Abschlussprüfung vorzubereiten, als er auf die Idee stieß, einen frequenzsortierten Binärbaum zu verwenden, und somit in kürzester Zeit jene Methode als effizienteste beweisen konnte.
Auf diese Weise übertraf Huffman seinen Professor Fano, der gemeinsam mit dem Begründer der Informationstheorie Claude Shannon einen ähnlichen Code entwickelte. Indem Huffman den Baum von unten nach oben anstatt von oben nach unten erstellte, vermied er die größte Schwachstelle der suboptimalen Shannon-Fano-Kodierung.[4]
Algorithmus[Bearbeiten | Quelltext bearbeiten]
Definitionen
- ist das Quellalphabet – der Zeichenvorrat, aus dem die Quellsymbole bestehen
- ist die A-priori-Wahrscheinlichkeit und relative Häufigkeit des Symbols (die relative Häufigkeit)
- ist das Codealphabet – der Zeichenvorrat, aus dem die Codewörter bestehen
- ist die Mächtigkeit des Codealphabetes – die Anzahl der verschiedenen Zeichen
Erzeugen des Baumes
- Ermittle für jedes Quellsymbol die relative Häufigkeit, d. h., zähle, wie oft jedes Zeichen vorkommt, und teile durch die Anzahl aller Zeichen.
- Erstelle für jedes Quellsymbol einen einzelnen Knoten (die einfachste Form eines Baumes) und notiere im Knoten die Häufigkeit.
- Wiederhole die folgenden Schritte so lange, bis nur noch ein einziger Baum übrig ist:
- Wähle die Teilbäume mit der geringsten Häufigkeit in der Wurzel, bei mehreren Möglichkeiten die Teilbäume mit der geringsten Tiefe.
- Fasse diese Bäume zu einem neuen (Teil-)Baum zusammen.
- Notiere die Summe der Häufigkeiten in der Wurzel.
Konstruktion des Codebuchs
- Ordne jedem Kind eines Knotens eindeutig ein Zeichen aus dem Codealphabet zu.
- Lies für jedes Quellsymbol (Blatt im Baum) das Codewort aus:
Kodierung
- Lies ein Quellsymbol ein.
- Ermittle das zugehörige Codewort aus dem Codebuch.
- Gib das Codewort aus.
Mittlere Wortlänge[Bearbeiten | Quelltext bearbeiten]
Die mittlere Länge eines Codeworts kann auf drei Arten berechnet werden.
- Über die gewichtete Summe der Codewortlängen:
- Die Summe aus der Anzahl der Schritte im Baum multipliziert mit der Häufigkeit eines Symbols.
- Indem man die Auftrittswahrscheinlichkeiten an allen Zwischenknoten des Huffman-Baums summiert.
- Bei ausschließlich gleicher Häufigkeit der zu codierenden Elemente ist die mittlere Länge
- mit als Anzahl der zu codierenden Elemente.
Beispiel[Bearbeiten | Quelltext bearbeiten]
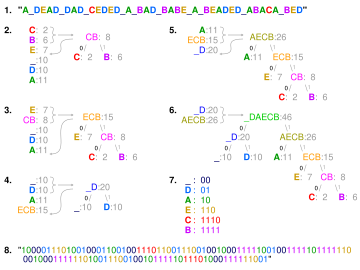
Das Quellalphabet sei . Als Codealphabet wählen wir den Binärcode und . Der Text soll komprimiert werden.
Zuerst werden die relativen Häufigkeiten bestimmt:
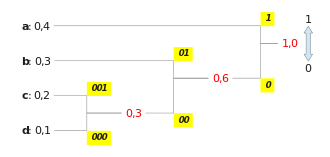
Es wird ein Huffman-Baum konstruiert und anschließend die Codewörter an den Kanten eingetragen (siehe Bild rechts).
Daraus ergibt sich folgendes Codebuch:
Mit diesem Codebuch wird der ursprüngliche Text kodiert:
| Originaltext | a | a | b | a | b | c | a | b | c | d |
| Kodierter Text | 1 | 1 | 01 | 1 | 01 | 001 | 1 | 01 | 001 | 000 |
Diese Huffman-Kodierung kodiert jedes Symbol mit durchschnittlich Bit. Das ist die mittlere Codewortlänge. Bei einer naiven Kodierung würde jedes der 4 Symbole mit Bit kodiert.
Die Entropie liegt bei
Bit je Symbol. Dadurch, dass der Informationsgehalt je Quellsymbol keine ganze Zahl ist, verbleibt bei der Kodierung eine Rest-Redundanz.
Dekodierung[Bearbeiten | Quelltext bearbeiten]
Zur Dekodierung eines Huffman-kodierten Datenstroms ist beim klassischen Verfahren das im Kodierer erstellte Codebuch notwendig. Grundsätzlich wird dabei umgekehrt als im Kodierungsschritt vorgegangen. Der Huffman-Baum wird im Dekodierer wieder aufgebaut und mit jedem eingehenden Bit – ausgehend von der Wurzel – der entsprechende Pfad im Baum abgelaufen, bis man an einem Blatt ankommt. Dieses Blatt ist dann das gesuchte Quellsymbol und man beginnt mit der Dekodierung des nächsten Symbols wieder an der Wurzel.
Beispiel[Bearbeiten | Quelltext bearbeiten]

Der Dekodierer hat das Codebuch
und die empfangene Nachricht 1101101001101001000.
Jetzt wird für jedes empfangene Bit ausgehend von der Wurzel der Pfad im Baum abgelaufen, bis ein Blatt erreicht wurde (siehe Abbildung). Sobald ein Blatt erreicht wurde, speichert der Dekodierer das Symbol des Blattes und beginnt wieder bei der Wurzel, bis das nächste Blatt erreicht wird. Daraus ergibt sich der dekodierte Text:
| Kodierter Text | 1 | 1 | 01 | 1 | 01 | 001 | 1 | 01 | 001 | 000 |
| Dekodierter Text | a | a | b | a | b | c | a | b | c | d |
Pseudocode[Bearbeiten | Quelltext bearbeiten]
Die folgenden Beispiele in Pseudocode zeigen Funktionen für die Generierung der Huffman-Kodierung.
Erzeugen des Baumes[Bearbeiten | Quelltext bearbeiten]
Diese Funktion erzeugt einen Huffman Tree als Min-Heap und gibt einen Zeiger auf den Wurzelknoten zurück. Die Knoten des Min-Heap werden in einer Vorrangwarteschlange gespeichert.
/**
* left // linker Kindknoten
* right // rechter Kindknoten
* top // Elternknoten
* minHeap // Vorrangwarteschlange für den Min-Heap
*/
function createHuffmanTree(symbolList, frequencyList, symbolsCount)
{
// Fügt die Knoten mit Symbol und Häufigkeit in die Vorrangwarteschlange ein
foreach (symbol in symbolList)
{
Knoten mit Symbol und Häufigkeit in minHeap einfügen
}
// Der HuffmanTree wird schrittweise erzeugt, bis sich alle Knoten einem Baum befinden und nur noch der Wurzelknoten in der Vorrangwarteschlange ist
while (die Anzahl der Knoten in minHeap ist nicht 1) // Solange die Anzahl der Knoten in der Vorrangwarteschlange nicht 1 ist
{
// Entfernt die zwei Knoten mit der kleinsten Häufigkeit aus der Vorrangwarteschlange
left := minHeap.top()
minHeap.pop()
right := minHeap.top()
minHeap.pop()
Erzeuge einen neuen inneren Knoten top mit der Summe der Häufigkeiten der zwei Knoten left->frequency und right->frequency
// Fügt die zwei Knoten mit der kleinsten Häufigkeit als linken und rechten Kindknoten des neuen inneren Knoten in den Baum ein
top->left := left
top->right := right
minHeap.push(top) // Fügt den neuen Knoten in die Vorrangwarteschlange ein
}
return minHeap.top() // Gibt einen Zeiger auf den Wurzelknoten zurück
}
Erzeugen des Codebuchs[Bearbeiten | Quelltext bearbeiten]
Diese rekursive Funktion erzeugt das Codebuch für die Huffman-Kodierung, indem sie jedem Symbol des Quellalphabet ein binäres Codewort als Zeichenkette zuordnet.
/**
* dictionary // Zuordnungstabelle für das Codebuch
*/
// Diese rekursive Funktion erzeugt das Codebuch für die Huffman-Kodierung und speichert es in der Variable dictionary
function createDictionary(node, codeword, dictionary)
{
if (der Knoten ist node ist leer)
{
return; // Abbruchbedingung, wenn kein linker oder rechter Teilbaum vorhanden ist
}
if (node->symbol is kein innerer Knoten, also ein Blatt) // Wenn der Knoten kein innerer Knoten, also ein Blatt ist
{
dictionary.insert(node->symbol, codeword); // Fügt die Kombination aus Symbol und Codewort dem Codebuch hinzu
}
createDictionary(node->left, concat(codeword, "0"), dictionary) // Rekusiver Aufruf für den linken Teilbaum, das Codesymbol 0 für die linke Kante wird angefügt
createDictionary(node->right, concat(codeword, "1"), dictionary) // Rekusiver Aufruf für den rechten Teilbaum, das Codesymbol 1 für die rechte Kante wird angefügt
}
Optimalität[Bearbeiten | Quelltext bearbeiten]
Für mittlere Codewortlänge eines Huffman-Codes gilt[5]
Das bedeutet, im Mittel benötigt jedes Codesymbol mindestens so viele Stellen wie sein Informationsgehalt, höchstens jedoch eine mehr.
gilt genau dann, wenn alle Wahrscheinlichkeiten Zweierpotenzen sind (). In dem Fall sagt man, die Huffman-Kodierung sei optimal bezüglich der Entropie.
Fasst man Quellsymbole zu einem großen Symbol zusammen, so gilt für die mittleren Codesymbollängen
- ,
das heißt, mit zunehmender Anzahl gemeinsam kodierter Quellsymbole geht die mittlere Codewortlänge asymptotisch gegen die Entropie – die Huffman-Kodierung ist asymptotisch optimal.
Diese Optimalität der Huffman-Kodierung lässt sich mit vollständiger Induktion beweisen.[6][7]
Laufzeit[Bearbeiten | Quelltext bearbeiten]
Sei die Anzahl der Zeichen des Originaltexts und die Anzahl der verschiedenen Zeichen. Die erste Anweisung, die die Häufigkeiten der Zeichen zählt, hat die asymptotische Laufzeit . Die for-Schleife iteriert über die verschiedenen Zeichen im Quellalphabet. Diese Schleife iteriert lediglich Mal und nicht Mal. Die while-Schleife beginnt mit einer Vorrangwarteschlange, die Elemente enthält, und reduziert diese in jeder Iteration um ein Element. Sie iteriert also Mal. In jeder Iteration ruft sie zweimal die Funktion pop und einmal die Funktion push auf, jeweils mit einer asymptotischen Laufzeit von bei Verwendung eines Heaps. Alle anderen Operationen innerhalb der while-Schleife sind in konstanter Laufzeit implementierbar. Die Laufzeit der while-Schleife ist also . Damit ist die Gesamtlaufzeit für die Huffman-Kodierung .[8]
Adaptive Huffman-Kodierung[Bearbeiten | Quelltext bearbeiten]
Die adaptive Huffman-Kodierung aktualisiert laufend den Baum. Der anfängliche Baum wird erzeugt, indem eine vorgegebene Wahrscheinlichkeitsverteilung für alle Quellsymbole angenommen wird (bei völliger Unkenntnis der Quelle eine Gleichverteilung). Mit jedem neuen Quellsymbol wird dieser aktualisiert, wodurch sich ggf. auch die Codesymbole ändern. Dieser Aktualisierungsschritt kann im Dekodierer nachvollzogen werden, so dass eine Übertragung des Codebuchs nicht nötig ist.
Mit dieser Methode kann ein Datenstrom on-the-fly kodiert werden. Er ist jedoch erheblich anfälliger für Übertragungsfehler, da ein einziger Fehler zu einer – ab der Fehlerstelle – komplett falschen Dekodierung führt.
Siehe auch[Bearbeiten | Quelltext bearbeiten]
- Arithmetisches Kodieren
- Bereichskodierung
- Shannon-Fano-Kodierung
- Tunstall-Kodierung
- Asymmetric Numeral Systems
- Context-Adaptive Binary Arithmetic Coding
Literatur[Bearbeiten | Quelltext bearbeiten]
- Thomas M. Cover, Joy A. Thomas: Elements of Information Theory
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Freie Universität Berlin, Institut für Informatik: Präfixcodes und der Huffman–Algorithmus
- Freie Universität Berlin, Institut für Informatik: Huffman-Kodierung
- SwissEduc: Huffman-Code
- LNTwww: Huffman- und Shannon-Fano-Codierung
- Huffman Coding Java (Codebeispiel in Java)
- Paul E. Black, National Institute of Standards and Technology: Huffman Coding, Dictionary of Algorithms and Data Structures.
- Huffman Tree Generator (Web Application)
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ D. A. Huffman: A method for the construction of minimum-redundancy codes. In: Proceedings of the I.R.E. September 1952, S. 1098–1101 (compression.ru [PDF]).
- ↑ David Wagner, University of California, Berkeley: Data Compression via Huffman Coding
- ↑ Northeastern University: Priority Queue; Heapsort; Huffman Code
- ↑ Profil: David A. Huffman
- ↑ Strutz: Bilddatenkompression, SpringerVieweg, 2009
- ↑ University of California, Berkeley: Proof of Optimality of Huffman Coding
- ↑ University of Toronto: Proof of Optimality of Huffman Codes
- ↑ Justus Piater, Universität Innsbruck: Huffman Coding: Algorithmus und Analyse
































