Wendelfläche

Ausschnitt einer Wendelfläche für $0\leq r\leq r_{0},0\leq \phi \leq \phi _{0}$

Die Wendelfläche oder Helikoide ist eine Fläche aus dem mathematischen Teilgebiet der Differentialgeometrie. Sie ist neben der Ebene die einzige einfach zusammenhängende Minimalfläche im 3-dimensionalen euklidischen Raum.

Parametrisierung

Ein Ausschnitt der Wendelfläche zum Parameter $c=1$. Der Ausschnitt zeigt den Teil für $-1\leq r\leq 1$ und $-\pi \leq \phi \leq \pi$.

Für eine fest gewählte Konstante $c>0$ parametrisiert man die Wendelfläche durch

$x=r\cos(\phi )$

$y=r\sin(\phi )$

$z=c\phi$,

wobei $r$ und $\phi$ alle reellen Werte annehmen, also von $-\infty$ bis $\infty$ laufen.

Minimalfläche

Die Hauptkrümmungen der Wendelfläche in dem den Parametern $r,\phi$ entsprechenden Punkt sind ${\frac {1}{1+r^{2}}}$ und $-{\frac {1}{1+r^{2}}}$, die mittlere Krümmung ist also in jedem Punkt null, die Wendelfläche ist eine Minimalfläche.

Topologisch ist sie homöomorph zur Ebene.

Lokal ist sie isometrisch zum Katenoid, sie ist aber nicht zu diesem homöomorph.

Sie ist eine Regelfläche und eine Schraubfläche. Sie lässt sich auch als Schiebfläche darstellen.

Praktische und wissenschaftliche Bedeutung – Chiralität

• 
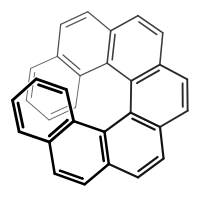
  Chemie: (P)-(+)-Heptahelicen weist Helizität im Uhrzeigersinn auf.
• 
  Chemie: (M)-(–)-Heptahelicen weist Helizität entgegen dem Uhrzeigersinn auf.
• 
  Wendeltreppe im Vatican-Museum in Rom als Beispiel für einen schraubenförmigen Baukörper zum Vergleich. Die Symmetrie entspricht der von (P)-Heptahelicen
• 
  Die Schraubendrehung dieser Kletterpflanze entspricht dem Drehsinn von (M)-Heptahelicen

In der Natur, in der Architektur und in der Chemie gibt es zahlreiche Anwendungsbereiche für Wendelflächen. Dabei spielt die Drehrichtung (Chiralität) auch eine Rolle.

Geschichte

Die Helikoide wurde im 18. Jahrhundert von Euler und Meusnier beschrieben. Catalan bewies 1842, dass sie neben der Ebene die einzige minimale Regelfläche ist. Meeks und Rosenberg bewiesen 2005 (aufbauend auf Ungleichungen von Colding-Minicozzi), dass es nur 2 Arten von einfach zusammenhängenden Minimalflächen im $\mathbb {R} ^{3}$ gibt: die Ebene und die Helikoide. Für von null verschiedenes topologisches Geschlecht fanden sich durch David Allen Hoffman und Kollegen in den 1990er Jahren aber weitere Beispiele, die aus der Helicoide hervorgingen. Den Beweis, dass sie für Genus 1 eine vollständige einbettbare Minimalfläche bilden, erbrachten Hoffman, Michael Wolf und Matthias Weber 2009 (davor war dies außer für den Fall des Geschlechts 0 nur für den Fall unendlichen Geschlechts bewiesen).

Weblinks

Commons: Helicoids – Sammlung von Bildern, Videos und Audiodateien

• Helicoid: Sammlung von Bildern und Animationen (Matthias Weber, Indiana University)