RANSAC-Algorithmus

RANSAC (englisch random sample consensus, deutsch etwa „Übereinstimmung mit einer zufälligen Stichprobe“) ist ein Resampling-Algorithmus zur Schätzung eines Modells innerhalb einer Reihe von Messwerten mit Ausreißern und groben Fehlern. Wegen seiner Robustheit gegenüber Ausreißern wird er vor allem bei der Auswertung automatischer Messungen vornehmlich im Fachgebiet Computer Vision eingesetzt. Hier unterstützt RANSAC – durch Berechnung einer um Ausreißer bereinigten Datenmenge, des sogenannten Consensus Sets – Ausgleichsverfahren wie die Methode der kleinsten Quadrate, die bei einer größeren Anzahl von Ausreißern meist versagen.

RANSAC wurde offiziell 1981 von Martin A. Fischler und Robert C. Bolles in den Communications of the ACM vorgestellt. Eine interne Präsentation am SRI International, an dem beide Autoren arbeiteten, fand bereits im März 1980 statt. Eine Alternative zu RANSAC sind M-Schätzer. Diese sind im Vergleich zu anderen Schätzern wie etwa den Maximum-Likelihood-Schätzern robuster gegenüber Ausreißern. RANSAC beruht auf wiederholtem zufälligem Subsampling.

Einleitung und Prinzip

Oft liegen als Ergebnis einer Messung Datenpunkte vor, die physikalische Werte wie Druck, Entfernung oder Temperatur, wirtschaftliche Größen oder ähnliches repräsentieren. In diese Punkte soll eine möglichst genau passende, parameterabhängige Modellkurve gelegt werden. Dabei liegen mehr Datenpunkte vor, als zur Ermittlung der Parameter notwendig sind; das Modell ist also überbestimmt. Die Messwerte können Ausreißer enthalten, also Werte, die nicht in die erwartete Messreihe passen. Da Messungen bis zur Entwicklung der Digitaltechnik meist manuell durchgeführt wurden, führte die Kontrolle durch den Operateur dazu, dass der Anteil von Ausreißern meist gering war. Die damals eingesetzten Ausgleichsalgorithmen, wie die Methode der kleinsten Quadrate, sind gut für die Auswertung solcher Datensätze mit wenig Ausreißern geeignet: Mit ihrer Hilfe wird zuerst mit der Gesamtheit der Datenpunkte das Modell bestimmt und danach versucht, die Ausreißer zu detektieren.

Der einzelne Ausreißer zieht die Ausgleichsgerade nach oben

Mit der Entwicklung der Digitaltechnik ab Anfang der 1980er Jahre änderten sich die Grundlagen. Durch die neuen Möglichkeiten wurden zunehmend automatische Messverfahren vor allem im Fachgebiet Computer Vision eingesetzt. Als Ergebnis liegt hier oft eine große Anzahl an Werten vor, die meist viele Ausreißer enthält. Die traditionellen Verfahren gehen von einer Normalverteilung der Fehler aus und liefern zum Teil kein sinnvolles Ergebnis, wenn die Datenpunkte viele Ausreißer enthalten. Dies ist in nebenstehender Darstellung illustriert. Es soll eine Gerade (das Modell) an die Punkte (Messwerte) angepasst werden. Der einzelne Ausreißer unter den 20 Datenpunkten kann einerseits durch traditionelle Verfahren vor Bestimmung der Gerade nicht ausgeschlossen werden. Andererseits beeinflusst er aufgrund seiner Lage die Ausgleichsgerade unverhältnismäßig stark (sogenannter Hebelpunkt).

Der RANSAC-Algorithmus verfolgt einen neuen, iterativen Ansatz. Statt alle Messwerte gemeinsam auszugleichen, werden lediglich so viele zufällig ausgewählte Werte benutzt, wie nötig sind, um die Modellparameter zu berechnen (im Fall einer Geraden wären das zwei Punkte). Dabei wird zunächst angenommen, dass die ausgewählten Werte keine Ausreißer sind. Diese Annahme wird überprüft, indem zuerst das Modell aus den zufällig gewählten Werten berechnet und danach die Distanz aller Messwerte (also nicht nur der ursprünglich ausgewählten) zu diesem Modell bestimmt wird. Ist die Distanz eines Messwertes zum Modell kleiner als ein vorher festgelegter Schwellenwert, dann ist dieser Messwert in Bezug auf das berechnete Modell kein grober Fehler. Er unterstützt es somit. Je mehr Messwerte das Modell unterstützen, desto wahrscheinlicher enthielten die zufällig zur Modellberechnung ausgewählten Werte keine Ausreißer. Diese drei Schritte – zufällige Auswahl von Messwerten, Berechnung der Modellparameter und Bestimmung der Unterstützung – werden mehrmals unabhängig voneinander wiederholt. In jeder Iteration wird gespeichert, welche Messwerte das jeweilige Modell unterstützen. Diese Menge wird Consensus Set genannt. Aus dem größten Consensus Set, das im Idealfall keine Ausreißer mehr enthält, wird abschließend mit einem der traditionellen Ausgleichsverfahren die Lösung ermittelt.

Anwendungen

Wie erwähnt, treten viele Ausreißer vor allem bei automatischen Messungen auf. Diese werden häufig im Fachgebiet Computer Vision durchgeführt, so dass RANSAC insbesondere hier weit verbreitet ist. Im Folgenden werden einige Anwendungen vorgestellt.

Gestitchtes Panoramabild von Alcatraz: Dazu müssen Einzelbilder passend überlagert werden, um sie danach zu überblenden. Dazu müssen gemeinsame Merkmale in den Teilbildern gefunden werden.

In der Bildverarbeitung wird RANSAC bei der Bestimmung von homologen Punkten zwischen zwei Kamerabildern eingesetzt. Homolog sind die zwei Bildpunkte, die ein einzelner Objektpunkt in den beiden Bildern erzeugt. Die Zuordnung homologer Punkte wird Korrespondenzproblem genannt. Das Resultat einer automatischen Analyse enthält meist eine größere Anzahl Fehlzuordnungen. Verfahren, die auf dem Ergebnis der Korrespondenzanalyse aufsetzen, benutzen RANSAC, um die Fehlzuordnungen auszuschließen. Ein Beispiel für diese Vorgehensweise ist die Erstellung eines Panoramabildes aus verschiedenen kleineren Einzelaufnahmen (Stitching). Ein weiteres ist die Berechnung der Epipolargeometrie. Das ist ein Modell aus der Geometrie, das die geometrischen Beziehungen zwischen verschiedenen Kamerabildern desselben Objekts darstellt. Hier dient RANSAC zur Bestimmung der Fundamentalmatrix, die die geometrische Beziehung zwischen den Bildern beschreibt.

Bei der DARPA Grand Challenge, einem Wettbewerb für autonome Landfahrzeuge, wurde RANSAC dazu benutzt, die Fahrbahnebene zu bestimmen sowie die Bewegung des Fahrzeuges zu rekonstruieren.

Der Algorithmus wird auch dazu verwendet, um in verrauschten dreidimensionalen Punktmengen geometrische Körper wie Zylinder oder ähnliches anzupassen oder automatisch Punktwolken zu segmentieren. Dabei werden alle Punkte, die nicht zum selben Segment gehören, als Ausreißer betrachtet. Nach einer Schätzung des dominantesten Körpers in der Punktwolke werden alle zu diesem Körper gehörenden Punkte entfernt, um im nächsten Schritt weitere Körper bestimmen zu können. Dieser Vorgang wird solange wiederholt, bis alle Körper in der Punktmenge gefunden wurden.

Vorgehensweise und Parameter

Voraussetzung für RANSAC ist, dass mehr Datenpunkte vorliegen, als zur Bestimmung der Modellparameter notwendig sind. Der Algorithmus besteht aus folgenden Schritten:

1. Wähle zufällig so viele Punkte aus den Datenpunkten, wie nötig sind, um die Parameter des Modells zu berechnen. Das geschieht in Erwartung, dass diese Menge frei von Ausreißern ist.
2. Ermittle mit den gewählten Punkten die Modellparameter.
3. Bestimme die Teilmenge der Messwerte, deren Abstand zur Modellkurve kleiner als ein bestimmter Grenzwert ist (diese Teilmenge wird Consensus Set genannt). Enthält sie eine gewisse Mindestanzahl an Werten, wurde vermutlich ein gutes Modell gefunden, und der Consensus Set wird gespeichert.
4. Wiederhole die Schritte 1–3 mehrmals.

Nach Durchführung von mehreren Iterationen wird diejenige Teilmenge gewählt, welche die meisten Punkte enthält (so denn eine gefunden wurde). Nur mit dieser Teilmenge werden mit einem der üblichen Ausgleichsverfahren die Modellparameter berechnet. Eine alternative Variante des Algorithmus beendet die Iterationen vorzeitig, wenn im Schritt 3 genügend Punkte das Modell unterstützen. Diese Variante wird als präemptives – das heißt vorzeitig abbrechendes – RANSAC bezeichnet. Bei diesem Vorgehen muss im Vorfeld bekannt sein, wie groß der Ausreißeranteil etwa ist, damit eingeschätzt werden kann, ob genügend Messwerte das Modell unterstützen.

Der Algorithmus hängt im Wesentlichen von drei Parametern ab:

1. dem maximalen Abstand eines Datenpunktes vom Modell, bis zu dem ein Punkt nicht als grober Fehler gilt;
2. der Anzahl der Iterationen und
3. der Mindestgröße des Consensus Sets, also der Mindestanzahl der mit dem Modell konsistenten Punkte.

Maximaler Abstand eines Datenpunkts vom Modell

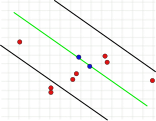
Dieser Parameter ist grundlegend für den Erfolg des Algorithmus. Im Gegensatz zu den anderen beiden Parametern muss er festgelegt werden (eine Überprüfung des Consensus Set braucht nicht durchgeführt zu werden, und die Anzahl der Iterationen kann nahezu beliebig hoch gewählt werden). Ist der Wert zu groß oder zu klein, kann der Algorithmus scheitern. Dies ist in den folgenden drei Bildern illustriert. Dargestellt ist jeweils ein Iterationsschritt. Die beiden zufällig ausgewählten Punkte, mit denen die grüne Modellgerade berechnet wurde, sind blau eingefärbt. Die Fehlerschranken sind als schwarze Linien dargestellt. Innerhalb dieser Linien muss ein Punkt liegen, um die Modellgerade zu unterstützen. Wird der Abstand zu groß gewählt, werden zu viele Ausreißer nicht erkannt, so dass ein falsches Modell die gleiche Anzahl von Ausreißern wie ein richtiges Modell haben kann (Bild 1a und 1b). Ist er zu gering angesetzt, kann es vorkommen, dass ein Modell, das aus einer ausreißerfreien Menge von Werten berechnet wurde, durch zu wenig andere Werte, die keine Ausreißer sind, unterstützt wird (Bild 2).

• Probleme bei zu großer oder zu kleiner Wahl der Fehlerschranke
• 
  1a. Richtige Lösung, zwei Punkte sind Ausreißer.
• 
  1b. Zweite, falsche Lösung mit der gleichen Anzahl von Ausreißern wie bei 1a.
• 
  2. Fehlerschranke zu klein.

Trotz dieser Probleme muss dieser Wert meist empirisch festgelegt werden. Lediglich wenn die Standardabweichung der Messwerte bekannt ist, kann die Fehlergrenze mittels der Gesetze der Wahrscheinlichkeitsverteilung berechnet werden.

Anzahl der Iterationen

Die Anzahl von Wiederholungen kann so festgelegt werden, dass mit einer bestimmten Wahrscheinlichkeit $p$ mindestens einmal eine ausreißerfreie Teilmenge aus den Datenpunkten ausgewählt wird. Ist $s$ die Anzahl der Datenpunkte, die zur Berechnung eines Modells notwendig sind, und $\epsilon$ der relative Anteil an Ausreißern in den Daten, so ist die Wahrscheinlichkeit, dass bei $n$ Wiederholungen nicht jedes Mal mindestens ein Ausreißer mit ausgewählt wird

$p=1-\left(1-\left(1-\epsilon \right)^{s}\right)^{n}$.

Damit die Wahrscheinlichkeit, dass jedes Mal mindestens ein Ausreißer mit ausgewählt wird, höchstens $1-p$ wird, muss $n$ groß genug gewählt werden. Genauer werden mindestens

$n={\frac {\log \left(1-p\right)}{\log \left(1-\left(1-\epsilon \right)^{s}\right)}}$

Wiederholungen benötigt. Die Anzahl hängt also nur vom Anteil der Ausreißer, der Zahl der Parameter der Modellfunktion und der vorgegebenen Wahrscheinlichkeit der Ziehung mindestens einer ausreißerfreien Teilmenge ab. Sie ist unabhängig von der Gesamtzahl der Messwerte.

In nachstehender Tabelle ist die notwendige Anzahl von Wiederholungen abhängig vom Ausreißeranteil und von der Anzahl der erforderlichen Punkte, die zur Bestimmung der Modellparameter erforderlich sind, dargestellt. Die Wahrscheinlichkeit, mindestens eine ausreißerfreie Teilmenge aus allen Datenpunkten auszuwählen, ist dabei mit 99 % festgelegt.

Anzahl der notwendigen Iterationen ($p=99\,\%$)

Beispiel	Anzahl der erforderlichen Punkte	Ausreißeranteil
		10 %	20 %	30 %	40 %	50 %	60 %	70 %
Gerade	2	3	5	7	11	17	27	49
Ebene	3	4	7	11	19	35	70	169
Fundamentalmatrix	8	9	26	78	272	1177	7025	70188

Größe des Consensus Sets

In der allgemeinen Variante des Algorithmus muss dieser Wert nicht zwangsläufig bekannt sein, da bei Verzicht auf eine Plausibilitätskontrolle einfach der größte Consensus Set im weiteren Verlauf benutzt werden kann. Seine Kenntnis ist aber für die vorzeitig abbrechende Variante notwendig. Bei dieser wird die Mindestgröße des Consensus Set meist analytisch oder experimentell bestimmt. Eine gute Näherung ist die Gesamtmenge der Messwerte, abzüglich des Anteils an Ausreißern $\epsilon$, der in den Daten vermutet wird. Für $n$ Datenpunkte ist die Mindestgröße gleich $(1-\epsilon )\cdot n$. Beispielsweise ist bei 12 Datenpunkten und 20 % Ausreißern die Mindestgröße näherungsweise 10.

Adaptive Bestimmung der Parameter

Der Anteil der Ausreißer an der Gesamtmenge der Datenpunkte ist oft unbekannt. Somit ist es nicht möglich, die benötigte Zahl der Iterationen und die Mindestgröße eines Consensus Set zu bestimmen. In diesem Fall wird der Algorithmus mit der Worst-Case-Annahme eines Ausreißeranteils von beispielsweise 50 % initialisiert und die Zahl der Iterationen und die Größe des Consensus Set entsprechend berechnet. Nach jeder Iteration werden die beiden Werte angepasst, wenn eine größere konsistente Menge gefunden wurde. Wird zum Beispiel der Algorithmus mit einem Ausreißeranteil von 50 % gestartet und enthält der berechnete Consensus Set aber 80 % aller Datenpunkte, ergibt sich ein verbesserter Wert für den Ausreißeranteil von 20 %. Die Zahl der Iterationen und die notwendige Größe des Consensus Set werden dann neu berechnet.

Beispiel

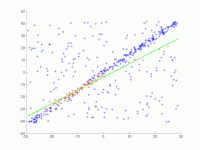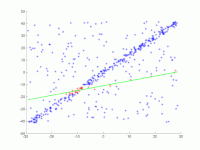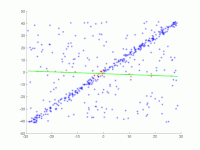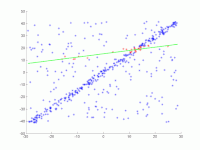
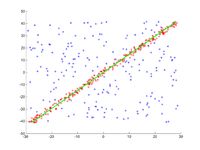
In eine Menge von Punkten in der Ebene soll eine Gerade angepasst werden. Die Punkte sind im ersten Bild dargestellt. Im zweiten Bild ist das Ergebnis verschiedener Durchgänge eingezeichnet. Rote Punkte unterstützen die Gerade. Punkte, deren Abstand zur Gerade größer als die Fehlerschranke ist, sind blau eingefärbt. Das dritte Bild zeigt die gefundene Lösung nach 1000 Iterationsschritten.

• RANSAC zum Anpassen einer Geraden an Datenpunkte
• 
  1. Original-Datensatz.
• 
  2. Animation mehrerer Iterationen.
• 
  3. Ergebnis nach 1000 Iterationen.

Weiterentwicklungen

Es gibt einige Erweiterungen von RANSAC, von denen hier zwei wichtige vorgestellt werden.

LO-RANSAC

Modellgerade wird nicht durch alle fehlerfreien Punkte unterstützt.

Es hat sich in Experimenten gezeigt, dass meist mehr Iterationsschritte als die theoretisch ausreichende Anzahl nötig sind: Wird mit einer ausreißerfreien Menge von Punkten ein Modell berechnet, so müssen nicht alle anderen Werte, die keine Ausreißer sind, dieses Modell unterstützen. Das Problem ist in nebenstehender Abbildung illustriert. Obwohl die Gerade mittels zweier fehlerfreier Werte berechnet wurde (schwarze Punkte), werden einige andere offensichtlich richtige Punkte rechts oben im Bild als Ausreißer (blaue Sterne) klassifiziert.

Aus diesem Grund wird der ursprüngliche Algorithmus bei LO-RANSAC (local optimised RANSAC) im Schritt 3 erweitert. Zuerst wird wie üblich die Teilmenge der Punkte bestimmt, die keine Ausreißer sind. Danach wird mittels dieser Menge und unter Zuhilfenahme eines beliebigen Ausgleichsverfahrens wie der Methode der kleinsten Quadrate das Modell nochmals bestimmt. Als letztes wird die Teilmenge berechnet, deren Abstand zu diesem optimierten Modell kleiner als die Fehlerschranke ist. Erst diese verbesserte Teilmenge wird als Consensus Set gespeichert.

MSAC

Bei RANSAC wird das Modell ausgewählt, welches durch die meisten Messwerte unterstützt wird. Dies entspricht der Minimierung einer Summe $C$, bei der alle fehlerfreien Werte mit 0 und alle Ausreißer mit einem konstanten Wert eingehen:

$C=\sum _{i}p({\text{Fehler}})\quad {\text{mit}}\quad p=\left\{{\begin{array}{ll}0,&{\text{wenn Fehler}}<{\text{Fehlerschranke}}\\{\text{konstant}}&{\text{wenn Fehler}}\geq {\text{Fehlerschranke}}\end{array}}\right.$

Das berechnete Modell kann sehr ungenau sein, wenn die Fehlerschranke zu hoch angesetzt wurde – je höher diese ist, desto mehr Lösungen haben gleiche Werte für $C$. Im Extremfall sind alle Fehler der Messwerte kleiner als die Fehlerschranke, so dass $C$ immer 0 ist. Damit können keine Ausreißer erkannt werden, und RANSAC liefert eine schlechte Schätzung.

MSAC (M-Estimator SAmple Consensus) ist eine Erweiterung von RANSAC, die eine modifizierte zu minimierende Zielfunktion benutzt:

$C=\sum _{i}p({\text{Fehler}})\quad {\text{mit}}\quad p=\left\{{\begin{array}{ll}{\text{Fehler,}}&{\text{wenn Fehler}}<{\text{Fehlerschranke}}\\{\text{konstanter Wert groesser als Fehlerschranke,}}&{\text{wenn Fehler}}\geq {\text{Fehlerschranke}}\end{array}}\right.$

Mit dieser Funktion erhalten Ausreißer weiterhin eine bestimmte „Strafe“, die größer als die Fehlerschranke ist. Werte unterhalb der Fehlerschranke gehen direkt mit dem Fehler anstelle von 0 in die Summe ein. Dadurch wird das angesprochene Problem beseitigt, da ein Punkt umso weniger zur Summe beiträgt, je besser er zum Modell passt.

Literatur

• Martin A. Fischler und Robert C. Bolles: Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography. (PDF; 1,2 MB) 1981, archiviert vom Original (nicht mehr online verfügbar) am 5. April 2019; abgerufen am 14. Oktober 2019. 
• Verschiedene Autoren: 25 Years of RANSAC, Workshop in conjunction with CVPR 2006. 2006, abgerufen am 11. März 2008. 
• Peter Kovesi: RANSAC – Robustly fits a model to data with the RANSAC algorithm (Matlab-Implementation). 2007, abgerufen am 11. März 2008. 
• Volker Rodehorst: Photogrammetrische 3D-Rekonstruktion im Nahbereich durch Auto-Kalibrierung mit projektiver Geometrie. wvb Wissenschaftlicher Verlag Berlin, 2004, ISBN 978-3-936846-83-6 (Hochschulschrift, zugl. Dissertation, TU Berlin 2004). 
• Richard Hartley, Andrew Zisserman: Multiple View Geometry in Computer Vision. 2. Auflage. Cambridge University Press, Cambridge, UK 2004, ISBN 978-0-521-54051-3 (englisch). 
• Tilo Strutz: Data Fitting and Uncertainty (A practical introduction to weighted least squares and beyond). 2nd edition Auflage. Springer Vieweg, 2016, ISBN 978-3-658-11455-8 (englisch).