Adjazenzliste
In der Graphentheorie sind Adjazenzlisten (oder auch Nachbarschaftslisten) eine Möglichkeit, Graphen zu repräsentieren. Dabei wird für jeden Knoten eine Liste, die Adjazenzliste, aller seiner Nachbarn (in ungerichteten Graphen) bzw. Nachfolger (in gerichteten Graphen) angegeben. Oft basieren Datenstrukturen für Graphen auf Adjazenzlisten. Im einfachsten Fall wird in einem Array für jeden Knoten eine einfach verkettete Liste aller Nachbarn gespeichert.
Definition[Bearbeiten | Quelltext bearbeiten]
Bei einem ungerichteten Graphen versteht man unter einer Adjazenzliste für einen Knoten eine Liste aller Nachbarn von , d. h. eine Liste der Knoten .
Bei einem gerichteten Graphen versteht man unter einer Adjazenzliste für einen Knoten eine Liste aller Nachfolger von , d. h. eine Liste der Knoten .
In beiden Fällen ist die Reihenfolge der Knoten in der Adjazenzliste beliebig. Eine Adjazenzlisten-Repräsentation eines Graphen erhält man, indem man für jeden Knoten eine Adjazenzliste angibt.
Beispiel 1[Bearbeiten | Quelltext bearbeiten]
Ein ungerichteter Graph mit Knoten und Kanten , und seine Repräsentation mit Hilfe von Adjazenzlisten.
| Graph | Adjazenzlisten |
|---|---|

|
a: d, b, d, e b: c, a c: b, d d: a, a, c e: a |
Beispiel 2[Bearbeiten | Quelltext bearbeiten]
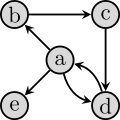
Ein gerichteter Graph mit Knoten und Kanten , und seine Repräsentation mit Hilfe von Adjazenzlisten.
| Graph | Adjazenzlisten |
|---|---|
|
a: b, d, e b: c c: d d: a e: |
Adjazenzlisten als Datenstrukturen[Bearbeiten | Quelltext bearbeiten]
Die Adjazenzlisten-Repräsentation von Graphen dient oft als Basis von Datenstrukturen für Graphen. Es gibt unterschiedliche Varianten diese Adjazenzlisten-Repräsentation in einer Datenstruktur umzusetzen, die auch unterschiedliche Verhalten der Datenstrukturen verursachen.
Einige Varianten:
- Knoten-Array mit Adjazenzlisten als verkettete Listen: Hier wird ein mit Knotenidentifikatoren indiziertes Array gespeichert, wobei in jedem Element des Arrays ein Zeiger auf die entsprechende Adjazenzliste gespeichert wird. Die Adjazenzlisten selbst werden als verkettete Listen gespeichert.
- Verkettete Liste von Knoten mit Adjazenzlisten als verkettete Listen: Die Knoten werden als verkettete Liste gespeichert und jeder Knoten enthält einen Zeiger auf die entsprechende Adjazenzliste. Die Adjazenzlisten selbst werden auch als verkettete Listen gespeichert.
Bei Verwendung einer naiven Array-Implementierung erfordert eine Adjazenzliste für einen ungerichteten Graphen etwa Bytes Speicherplatz, wobei die Anzahl der Kanten des Graphen ist. In der Adjazenzmatrix der Hauptalternative zur Adjazenzliste benötigt jeder Eintrag in der Adjazenzmatrix nur ein Bit. Eine Adjazenzmatrix kann daher sehr kompakt in nur Bytes zusammenhängenden Speicher repräsentiert werden, wobei die Anzahl der Knoten des Graphen ist. Diese Kompaktheit fördert auch die Lokalität der Referenzen. Für einen dünnen Graphen benötigen Adjazenzlisten jedoch weniger Speicherplatz. Berücksichtigt man, dass ein ungerichteter einfacher Graph höchstens Kanten haben kann, was Schleifen zulässt, kann man die Dichte des Graphen mit bezeichnen. Dann ist , wenn , d. h. die Darstellung als Adjazenzliste nimmt mehr Platz ein als die Darstellung als Adjazenzmatrix, wenn . Daher muss ein Graph dünn genug sein damit eine Darstellung der Adjazenzliste kompakter als eine Darstellung als Adjazenzmatrix ist.
Die unterschiedlichen Repräsentationen erleichtern auch unterschiedliche Operationen. Das Finden aller benachbarten Knoten eines bestimmten Knotens mit Adjazenzlisten ist so einfach wie das Lesen der entsprechenden Adjazenzliste und daher proportional zum Grad. Bei einer Adjazenzmatrix muss stattdessen eine ganze Zeile gelesen werden und daher proportional zur Gesamtanzahl der Knoten. Ob es eine Kante zwischen zwei gegebenen Knoten gibt, kann direkt aus der Adjazenzmatrix bestimmt werden, während mit Adjazenzlisten eine Laufzeit proportional zum Minimalgrad der beiden Knoten benötigt wird.
Beispiele[Bearbeiten | Quelltext bearbeiten]
Knoten-Array mit Adjazenzlisten als einfach verkettete Listen[Bearbeiten | Quelltext bearbeiten]
| Graph | Adjazenzlisten | Datenstruktur |
|---|---|---|

|
a: d, b, d, e b: c, a c: b, d d: a, a, c e: a |

|

|
a: b, d, e b: c c: d d: a e: |

|
Knoten-Array mit Adjazenzlisten als doppelt verkettete Listen[Bearbeiten | Quelltext bearbeiten]
| Graph | Adjazenzlisten | Datenstruktur |
|---|---|---|

|
a: d, b, d, e b: c, a c: b, d d: a, a, c e: a |

|

|
a: b, d, e b: c c: d d: a e: |

|
Verkettete Liste von Knoten mit Adjazenzlisten als einfach verkettete Listen[Bearbeiten | Quelltext bearbeiten]
| Graph | Adjazenzlisten | Datenstruktur |
|---|---|---|

|
a: d, b, d, e b: c, a c: b, d d: a, a, c e: a |
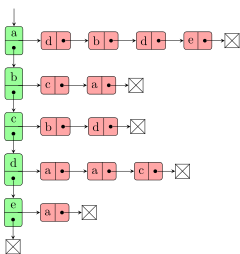
|

|
a: b, d, e b: c c: d d: a e: |

|
Siehe auch[Bearbeiten | Quelltext bearbeiten]
Literatur[Bearbeiten | Quelltext bearbeiten]
- Robert Sedgewick, Kevin Wayne: Algorithmen: Algorithmen und Datenstrukturen. 4. Auflage. Hallbergmoos: Pearson, 2014, ISBN 978-3-86894-184-5, S. 559–563.
- Thomas H. Cormen, Charles Leiserson, Ronald L. Rivest, Clifford Stein: Introduction to Algorithms. 3. Auflage. MIT Press and McGraw-Hill, 2009, ISBN 978-0-262-53305-8, S. 589–593.
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Eric W. Weisstein: Adjacency List. In: MathWorld (englisch).
















