Benutzer:Pyrometer/Baustelle/Scratch/Sratchpad
Umrechnungen
[Bearbeiten | Quelltext bearbeiten]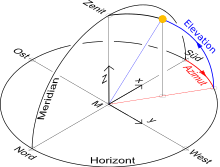
nördliche Erdkugelhälfte,
(x,y,z) und (a,h)

nördliche Erdkugelhälfte,
(x',y',z') und (τ,δ)
horizontale (a, h) → kartesische Koordinaten → ruhende äquatoriale Koordinaten (τ, δ)
[Bearbeiten | Quelltext bearbeiten]Im äquatorialen x,y,z-System
x = cos δ · cos τ y = cos δ · sin τ (1) z = sin δ
Im horizontalen x',y',z'-System
x' = cos h · cos a y' = cos h · sin a (2) z' = sin h
Rotation des x'-System um 90°-φ um die y-Achse identifiziert es mit dem x,y,z-System:
Transformationsmatrix für eine Rotation um die y-Achse um den Winkel α
cos α 0 sin α 0 1 0 (3) -sin α 0 cos α
Die Anwendung der Matrix (3) auf Koordinaten (x', y', z') des äquatorialen Systems mit einem Drehwinkel von (90°-φ) um die y-Achse ...
x = x' * cos (90°-φ) + z' * sin (90°-φ) y = y' (4) z = -x' * sin (90°-φ) + z' * cos (90°-φ)
Mit cos(α) = cos(-α) und sin(α) = -sin(-α) sowie cos (α-90°) = sin (α) und sin (α-90°) = cos (α) gelten
cos (90°-α) = cos (α-90°) = sin (α) (4.1) sin (90°-α) = -sin (α-90°) = cos (α)
(4.1) angewendet auf (4) ergibt
x = x' * sin φ + z' * cos φ y = y' (4.2) z = -x' * cos φ + z' * sin φ
(2) eingesetzt in (4.2) liefert (5)
x = cos h · cos a * sin φ + sin h * cos φ y = cos h · sin a (5) z = -cos h · cos a * cos φ + sin h * sin φ
(5) gleichgesetzt mit (1) liefert
x = cos δ · cos τ = cos h · cos a * sin φ + sin h * cos φ y = cos δ · sin τ = cos h · sin a (6) z = sin δ =-cos h · cos a * cos φ + sin h * sin φ
Division (6b)/(6a) liefert
sin τ cos h · sin a
----- = ------------------------------------- =
cos τ cos h · cos a * sin φ + sin h * cos φ
sin a
= tan τ = ----------------------------- (7)
cos a * sin φ + tan h * cos φ
und endlich
τ = atan2 ( sin a / (cos a * sin φ + tan h * cos φ) ) (8)
aus (5c) folgt
δ = arcsin ( -cos h · cos a * cos φ + sin h * sin φ ) (9) δ = arcsin ( sin φ * sin h - cos φ * cos h · cos a )
Die "Originalformeln" aus dem Artikel lauten übereinstimmend:
x = cos δ · cos τ = sin φ · cos h · cos a + cos φ · sin h (siehe (6)) y = cos δ · sin τ = cos h · sin a z = sin δ = sin φ · sin h - cos φ · cos h · cos a z = sin δ =-cos φ · cos h · cos a + sin φ · sin h
δ = arcsin ( sin φ · sin h - cos φ · cos h · cos a ) (siehe 9) τ = arctan ( sin a / (sin φ · cos a + cos φ · tan h) ) (siehe 8)
Herleitung mit Hilfe des nautischen Dreiecks
[Bearbeiten | Quelltext bearbeiten]
Punkt F (Frühlingspunkt?) ohne Bedeutung
Das nautische Dreieck ist das Kugeldreieck an der Himmelskugel zwischen folgenden Eckpunkten:
- Zenit (Ze)
- Himmelsnordpol (NP)
- Gestirn (St)
Seine Seiten und Winkel stehen mit den Himmelskoordinaten in direktem Zusammenhang:
- Seitenlänge Zenit - Himmelsnordpol:
- Seitenlänge Himmelsnordpol - Gestirn:
- Seitenlänge Zenit - Gestirn:
- Winkel am Zenit:
- Winkel am Himmelsnordpol:
- Erklärung der Formelzeichen
| Größe | Definition | Bedeutung |
|---|---|---|
| Rektaszension des Gestirns (vom Frühlingspunkt an östlich gezählt) | Himmelssystem , äquatorial, rotierend. Fest am "Sternenzelt". Wird für Stern-Kataloge und -Karten verwendet. | |
| Deklination des Gestirns (Höhe über Himmelsäquator) | ||
| Sternzeit (abhängig von der Beobachtungszeit und von der geographischen Länge des Beobachtungsortes) | Beschreibt den Drehwinkel des rotierenden äquatorialen Systems gegenüber der Südrichtung des Beobachters (also gegen dessen ruhendes äquatoriales System). | |
| Stundenwinkel (von der Südrichtung (Meridian) aus nach Westen | Ortsäquator-System , äquatorial, ruhend. Rotiert mit Erde um Polachse gegen Himmelszelt. Fixsterne wandern über einen Tag bei konstantem | |
| Geographische Breite des Beobachters (gezählt nördlich über Äquator) | Der Breitengrad bestimmt die Neigung der beiden Äquatorsysteme und gegen das Horizontsystem | |
| Azimut (von Süden an westlich gezählt) | Horizontsystem fest am Beobachter | |
| Höhe (Höhe über dem Horizont) |
Das nautische Dreieck erlaubt die direkte Ermittlung von Koordinatentransformationen zwischen verschiedenen Kugelkoordinatensystemen mittels der Sätze der sphärischen Trigonometrie.
Hergeleitet wird dieses Zeug womöglich gar nicht über den Zwischenschritt zu den kartesischen Koordinaten, sondern direkt aus den Gesetzen im Kugeldreieck. Dabei wird (ich finde das sehr elegant!) mit dem nautischen Dreieck gearbeitet.
- Horizontalsystem -> Äquatorialsystem
- Äquatorialsystem -> Horizontalsystem
Nachweis zu Variante mit Signum:
[Bearbeiten | Quelltext bearbeiten]Statt mit Quadrantenbestimmung kann man viel eleganter mit schreiben.
Neuere Ab schnitt
[Bearbeiten | Quelltext bearbeiten]ynf g-ydfhgia





















