Fehler 1. und 2. Art
Die Fehler 1. und 2. Art, auch α-Fehler (Alpha-Fehler) und β-Fehler (Beta-Fehler) genannt, bezeichnen eine statistische Fehlentscheidung bei statistischen Tests. Sie beziehen sich auf eine Methode der mathematischen Statistik, den sogenannten Hypothesentest. Beim Test einer Hypothese liegt ein Fehler 1. Art vor, wenn die Nullhypothese zurückgewiesen wird, obwohl sie in Wirklichkeit wahr ist (beruhend auf einer zufällig erhöhten bzw. niedrigeren Anzahl positiver Ergebnisse). Dagegen bedeutet ein Fehler 2. Art, dass der Test die Nullhypothese fälschlicherweise nicht zurückweist, obwohl die Alternativhypothese korrekt ist. Die Fehlerwahrscheinlichkeiten 1. und 2. Art (auch α- und β-Risiko genannt) werden in Qualitätsmanagement und -kontrolle häufig Produzentenrisiko und Konsumentenrisiko genannt (siehe Prüflos). In der statistischen Prozesslenkung durch Qualitätsregelkarten verwendet man dafür die Begriffe blinder Alarm und unterlassener Alarm. Fehler 1. und 2. Art werden auch als frequentistische Konzepte bezeichnet.[1] Das Konzept des Fehlers 1. und 2. Art wurde von Neyman und Pearson eingeführt.[2]
Entscheidungstabelle
[Bearbeiten | Quelltext bearbeiten]| Wirklichkeit | |||
|---|---|---|---|
| H0 ist wahr | H1 ist wahr | ||
| Entscheidung des Tests … |
… für H0 | Richtige Entscheidung (Spezifität) (richtig negativ) Wahrscheinlichkeit: 1 − α |
Fehler 2. Art (falsch negativ) Wahrscheinlichkeit: β |
| … für H1 | Fehler 1. Art (falsch positiv) Wahrscheinlichkeit: α |
Richtige Entscheidung Wahrscheinlichkeit: 1 − β (richtig positiv) (Trennschärfe des Tests, Sensitivität) | |
Formale Darstellung
[Bearbeiten | Quelltext bearbeiten]Ein statistischer Test ist ein Entscheidungsproblem, bei dem es um einen unbekannten Parameter geht, der in einem bestimmten Parameterraum liegen muss. Der Parameterraum kann in zwei disjunkte Teilmengen und zerlegt werden. Das Entscheidungsproblem liegt nun darin zu entscheiden, ob in oder liegt. Bezeichne die Nullhypothese und die Alternativhypothese. Da und disjunkt sind, kann nur eine der beiden Hypothesen wahr sein. Da das Ziel des Hypothesentests eine Entscheidung ist, gibt es Wahrscheinlichkeiten dafür, dass man eine falsche Entscheidung trifft. Seien und . Wenn Ablehnbereich und Teststatistik definiert wurden, dann kann die Wahrscheinlichkeit abzulehnen für jedes bestimmt werden. Sei [3], wobei abgelehnt wird, wenn die Teststatistik in den kritischen Bereich fällt, also gilt. Die Funktion für wird auch Gütefunktion genannt.
Ein Fehler 1. Art liegt vor, wenn die Nullhypothese abgelehnt wird, obwohl diese richtig ist. Dem Fehler erster Art können die Fehlerwahrscheinlichkeiten 1. Art, das sind die Wahrscheinlichkeiten für , mit denen es zu einem Fehler 1. Art kommt, zugeordnet werden. Es gibt also im Allgemeinen nicht die Fehlerwahrscheinlichkeit 1. Art, sondern im Fall einer zusammengesetzten Nullhypothese mehrere Fehlerwahrscheinlichkeiten 1. Art. Bei Hypothesentests ist es üblich, Testverfahren so zu konstruieren, dass die Fehlerwahrscheinlichkeiten 1. Art durch eine vorgegebene Konstante nach oben beschränkt wird, die das Signifikanzniveau oder die zugelassene Irrtumswahrscheinlichkeit[4][5] des Tests genannt wird. Es gilt also für alle . Ein Test mit dieser Eigenschaft heißt Signifikanztest zum Niveau , kurz Niveau--Test[4] oder -Niveau-Test.[6] Bei einer einfachen Nullhypothese kann der Test in der Regel so konstruiert werden, dass gilt, dann fällt die – in diesem Spezialfall eindeutige – Fehlerwahrscheinlichkeit 1. Art mit dem Signifikanzniveau zusammen. Bei einer zusammengesetzten Nullhypothese ist es häufig möglich, den Test so konstruieren, dass gilt.[7][8] Man sagt dann, dass der Test das Signifikanzniveau ausschöpft. Das Signifikanzniveau ist dann der größte Wert von im Bereich der Nullhypothese, also für alle .
Ein Fehler 2. Art liegt vor, wenn die Nullhypothese nicht abgelehnt wird, obwohl sie falsch ist. Die Fehlerwahrscheinlichkeiten 2. Art sind durch die Wahrscheinlichkeiten für gegeben. Im Gegensatz zum Fehler 1. Art wird der Fehler 2. Art nicht durch eine vorgegebene Schranke für die Fehlerwahrscheinlichkeiten 2. Art kontrolliert. Es ist i. A. nicht möglich, beide Fehlerwahrscheinlichkeiten gleichzeitig zu minimieren. Daher sucht man unter allen Signifikanztests (Tests, die für einen Fehler 1. Art kontrollieren) denjenigen, der die Fehlerwahrscheinlichkeiten 2. Art minimiert. Mit anderen Worten: Wenn das Signifikanzniveau als Schranke für den Fehler 1. Art a priori festgelegt wurde, dann ist man daran interessiert, die Trennschärfe gegen alle relevanten Alternativen zu maximieren. Die Trennschärfe eines Tests ist bestimmt durch die Komplemente der Fehlerwahrscheinlichkeiten 2. Art, d. h. durch für . Eine große Trennschärfe bedeutet also eine kleine Fehlerwahrscheinlichkeit 2. Art.
Die Fehlerwahrscheinlichkeit 2. Art ist abhängig von dem in der Grundgesamtheit vorliegenden Parameter.[9] Zusammenfassend gilt für die Fehlerwahrscheinlichkeiten 1. Art
und die Fehlerwahrscheinlichkeiten 2. Art sind durch
gegeben[10][11][12] Die Fehlerwahrscheinlichkeiten 2. Art werden auch Betafehler genannt und mit bezeichnet. Im Allgemeinen gilt, dass eine Verringerung von die Wahrscheinlichkeit eines Fehlers 2. Art erhöht und umgekehrt. Durch komplizierte Berechnungen kann auch bestimmt werden.
Im Spezialfall einer einfachen Nullhypothese und einer einfachen Gegenhypothese , wie er häufig bei medizinischen Test vorliegt, bei denen z. B. über 'krank' oder 'gesund', 'infiziert' oder 'nicht Infiziert' entschieden wird, gibt es die Fehlerwahrscheinlichkeit 1. Art und die Fehlerwahrscheinlichkeit 2. Art .
Fehler 1. Art
[Bearbeiten | Quelltext bearbeiten]Beim Test einer Hypothese liegt ein Fehler 1. Art vor, wenn die Nullhypothese zurückgewiesen wird, obwohl sie in Wirklichkeit wahr ist (beruhend auf falsch positiven Ergebnissen).
Die Ausgangshypothese (Nullhypothese) ist hierbei die Annahme, die Testsituation befinde sich im „Normalzustand“. Wird also dieser „Normalzustand“ nicht erkannt, obwohl er tatsächlich vorliegt, ergibt sich ein Fehler 1. Art. Beispiele für einen Fehler 1. Art sind:
- der Patient wird als krank angesehen, obwohl er in Wirklichkeit gesund ist (Nullhypothese: der Patient ist gesund),
- der Angeklagte wird als schuldig verurteilt, obwohl er in Wirklichkeit unschuldig ist (Nullhypothese: der Angeklagte ist unschuldig),
- der Person wird kein Zugang gewährt, obwohl sie eine Zugangsberechtigung hat (Nullhypothese: die Person hat Zugangsberechtigung)
Als Signifikanzniveau oder Irrtumswahrscheinlichkeit bezeichnet man die vor einem Hypothesentest festgelegte maximale Wahrscheinlichkeit dafür, dass die Nullhypothese aufgrund der Testergebnisse abgelehnt wird, obwohl die Nullhypothese wahr ist. In der Regel wählt man ein Signifikanzniveau von 5 % (signifikant) oder 1 % (sehr signifikant).
Die andere mögliche Fehlentscheidung, nämlich die Alternativhypothese zurückzuweisen, obwohl sie wahr ist, heißt Fehler 2. Art.
Beispiele
[Bearbeiten | Quelltext bearbeiten]- Ein Tester hat eine Urne vor sich, in die er nicht hineinschauen kann. Darin befinden sich rote und grüne Kugeln. Es kann jeweils nur eine Kugel zu Testzwecken aus der Urne entnommen werden.
Alternativhypothese: „In der Urne befinden sich mehr rote als grüne Kugeln“.
Um ein Urteil über den Inhalt der Urne abgeben zu können, wird der Tester der Urne mehrmals Kugeln zu Testzwecken entnehmen. Wenn er daraufhin zu der Entscheidung gelangt, dass die Alternativhypothese zutreffend sein kann, also er die Meinung vertritt, dass mehr rote als grüne Kugeln in der Urne seien, obwohl in Wirklichkeit die Nullhypothese zutrifft, nämlich dass gleich viele rote wie grüne oder weniger rote als grüne Kugeln in der Urne sind, dann begeht er einen Fehler 1. Art. - Wir wollen überprüfen, ob eine neue Lernmethode die Lernleistung von Schülern steigert. Dafür vergleichen wir eine Gruppe von Schülern, die nach der neuen Lernmethode unterrichtet wurden, mit einer Stichprobe von Schülern, die nach der alten Methode unterrichtet wurden.
Alternativhypothese: „Schüler, die nach der neuen Lernmethode unterrichtet wurden, haben eine höhere Lernleistung als Schüler, die nach der alten Methode unterrichtet wurden.“
Angenommen in unserer Untersuchung weist die Stichprobe von Schülern, die nach der neuen Lernmethode unterrichtet wurden, tatsächlich eine bessere Lernleistung auf. Vielleicht beruht dieser Unterschied aber auch nur auf Zufall oder anderen Einflüssen. Wenn also in Wahrheit zwischen den beiden Populationen überhaupt kein Unterschied besteht und wir fälschlicherweise die Nullhypothese verwerfen – es also als gesichert ansehen, dass die neue Methode das Lernen verbessert – dann begehen wir einen Fehler 1. Art. Dieser kann natürlich fatale Folgen haben, wenn wir z. B. mit hohen Kosten und viel Aufwand den gesamten Unterricht auf die neue Lernmethode umstellen, obwohl diese in Wahrheit überhaupt keine besseren Ergebnisse bewirkt. - Spam-Filter für ankommende E-Mails: Ein Filter soll erkennen, ob eine E-Mail Spam ist oder nicht.
Nullhypothese: Es ist eine normale E-Mail und kein Spam.
Alternativhypothese: Es ist Spam.
Falls eine E-Mail als Spam klassifiziert wird, sie jedoch in Wirklichkeit kein Spam ist, die E-Mail also falsch als Spam klassifiziert wird, so sprechen wir von einem Fehler 1. Art (falsch-positiv).
Fehler 2. Art
[Bearbeiten | Quelltext bearbeiten]Im Gegensatz zum Fehler 1. Art bedeutet ein Fehler 2. Art, dass der Test die Nullhypothese fälschlicherweise bestätigt, obwohl die Alternativhypothese korrekt ist.
Schwierigkeiten bei der Bestimmung des Fehlers 2. Art
[Bearbeiten | Quelltext bearbeiten]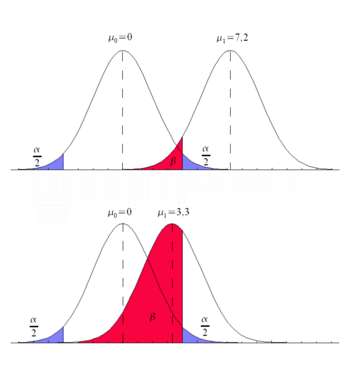
Im Gegensatz zum Risiko 1. Art, die gegebene Nullhypothese, obwohl sie in Wirklichkeit zutrifft, irrtümlicherweise abzulehnen, lässt sich das Risiko 2. Art, also die Wahrscheinlichkeit eines Fehlers 2. Art meist nicht vorab bestimmen. Grund dessen ist die Art und Weise der Festlegung von Hypothesen statistischer Tests: Während die Nullhypothese stets eine dezidierte Aussage wie beispielsweise : „Mittelwert“ darstellt, ist die Alternativhypothese, da sie im Grunde alle übrigen Möglichkeiten erfasst, damit i. d. R. auch nur recht unbestimmter bzw. globaler Natur (bspw. : „Mittelwert “).
Die rechtsstehende Grafik illustriert diese Abhängigkeit der Wahrscheinlichkeit eines Fehlers 2. Art ; (rot) vom unbekannten Mittelwert , wenn als „Signifikanzniveau“, d. h. maximales Risiko 1. Art, ; (blau) in beiden Fällen derselbe Wert gewählt wird. Wie zu sehen, ergibt sich dabei überdies die paradoxe Situation, dass die Wahrscheinlichkeit eines Fehlers 2. Art umso größer wird, je näher der wahre Wert an dem von der Nullhypothese behaupteten Wert liegt, bis hin dazu, dass für das Risiko 2. Art ; den Grenzwert ; annimmt. Anders gesagt: Je kleiner die Abweichung des tatsächlichen vom behaupteten Wert , desto größer paradoxerweise die Wahrscheinlichkeit, einen Fehler zu machen, wenn man aufgrund des Testergebnisses weiterhin dem behaupteten Wert Glauben schenkt (obwohl die Abweichung beider Werte voneinander möglicherweise aufgrund ihrer Geringfügigkeit praktisch gar keine Rolle mehr spielt). Wie dieser Widerspruch zeigt, kann ein rein formal-logischer Umgang mit der Problematik des Fehlers 2. Art leicht Grundlage von Fehlentscheidungen sein. Bei biometrischen und medizinstatistischen Anwendungen heißt die Wahrscheinlichkeit, eine Entscheidung für H0 zu treffen, falls H0 richtig ist, Spezifität. Die Wahrscheinlichkeit, eine Entscheidung für H1 zu treffen, falls H1 richtig ist, wird Sensitivität genannt. Wünschenswert ist, dass ein Testverfahren hohe Sensitivität und hohe Spezifität und damit kleine Wahrscheinlichkeiten für die Fehler erster und zweiter Art hat.
Beispiele
[Bearbeiten | Quelltext bearbeiten]- Im Six-Sigma-Projektmanagement: Fehler 1. Art: Man stellt am Projektende fest, dass bei der initialen Planung Aspekte ausgelassen wurden („zu wenig gemacht“). Ein Fehler 2. Art wäre hier, dass das gesamte Projekt über Dinge gemacht wurden, die sich am Ende als überflüssig bzw. irrelevant für den Projekterfolg herausstellen („zu viel gemacht“).
- Ein Tester hat eine Urne vor sich, in die er nicht hineinschauen kann. Darin befinden sich rote und grüne Kugeln. Es kann jeweils nur eine Kugel zu Testzwecken aus der Urne entnommen werden.
Alternativhypothese: „In der Urne befinden sich mehr rote als grüne Kugeln“.
Um ein Urteil über den Inhalt der Urne abgeben zu können, wird der Tester der Urne mehrmals Kugeln zu Testzwecken entnehmen. Die Nullhypothese in unserem Beispiel lautet, dass entweder genauso viele rote wie grüne, oder aber mehr grüne als rote Kugeln in der Urne sind (das Gegenteil der Alternativhypothese). Wenn der Tester aufgrund seiner Stichprobe also zu dem Schluss kommt, die Nullhypothese sei richtig bzw. die Alternativhypothese falsch, obwohl in Wahrheit doch die Alternativhypothese richtig ist, dann beginge er einen Fehler 2. Art. - Wir möchten den Einfluss der Ernährung auf die geistige Entwicklung von Kindern in Kinderheimen untersuchen. Dafür vergleichen wir zwei Gruppen von Kindern hinsichtlich ihrer Leistung in kognitiven Tests: Die eine Stichprobe wird nach dem herkömmlichen Plan ernährt, die andere erhält eine besonders gesunde Kost. Wir vermuten, dass die gesunde Kost sich positiv auf die kognitiven Leistungen auswirkt.
Alternativhypothese: „Kinder, die eine besonders gesunde Kost erhalten, weisen bessere kognitive Leistung auf als Kinder, die auf die herkömmliche Weise ernährt werden.“
Wenn wir nun die kognitive Leistung unserer beiden Stichproben vergleichen, so stellen wir keinen Unterschied in der kognitiven Leistung fest. Demzufolge halten wir die Alternativhypothese für falsch und bestätigen die Nullhypothese. Wenn jedoch in Wahrheit die Population der gesund Ernährten doch eine bessere Leistung aufweist, dann begehen wir einen Fehler 2. Art.
Aber wir haben in unserer Stichprobe doch keinen Unterschied festgestellt? Diese Gleichheit kann aber auch auf die zufällige Streuung der Messergebnisse oder auf die ungünstige Zusammenstellung unserer Stichproben zurückzuführen sein.
Das Begehen eines Fehlers 2. Art ist in der Regel weniger „schlimm“, als ein Fehler 1. Art. Dies hängt jedoch individuell vom Untersuchungsgegenstand ab. In unserem Beispiel hat der Fehler 2. Art ausgesprochen nachteilige Konsequenzen: Obwohl die gesunde Ernährung die Leistung verbessert, entscheiden wir uns, die herkömmliche Ernährung beizubehalten. Ein Fehler 1. Art, also die Einführung der gesunden Ernährung für alle Kinder, obwohl diese keine Leistungsverbesserung bringt, hätte hier weniger nachteilige Konsequenzen gehabt.
Terminologie bei medizinischen Tests
[Bearbeiten | Quelltext bearbeiten]- Die Nullhypothese ist in der Regel einfach, wie z. B. , und nicht zusammengesetzt, wie z. B. oder , dabei bedeutet die Nullhypothese je nach Fragestellung kein Effekt, kein Unterschied, keine Wirkung, nicht erkrankt, nicht infiziert usw. Durch Ablehnung der Nullhypothese wird versucht, einen Effekt, einen Unterschied, eine Wirkung, eine Erkrankung, eine Infektion usw. nachzuweisen.
- Ein beobachtetes Testergebnis heißt Befund. Ein Befund, der zur Ablehnung der Nullhypothese führt, heißt positiver Befund, anderenfalls negativer Befund.
- Ein Fehler 1. Art heißt falsch-positive Entscheidung oder falsch-positive Diagnose, ein Fehler 2. Art heißt falsch-negative Entscheidung oder falsch-negative Diagnose.
- Bei einem Test mit einfacher Null- und einfacher Alternativhypothese gibt es nur eine Fehlerwahrscheinlichkeit 1. Art, die als 'der' -Fehler und nur eine Fehlerwahrscheinlichkeit 2. Art, die als 'der' -Fehler bezeichnet werden. In diesem Fall heißt das Komplement der Fehlerwahrscheinlichkeit 1. Art die Spezifität des Tests und das Komplement der Fehlerwahrscheinlichkeit 2. Art – die Trennschärfe, Macht oder Güte des Tests in statistischer Terminologie – heißt die Sensitivität des Tests. Die Sensitivität des Tests ist die Wahrscheinlichkeit einer richtigen positiven Diagnose. Die Spezifität des Tests ist die Wahrscheinlichkeit einer richtigen negativen Diagnose.
Ergänzende Bemerkungen
[Bearbeiten | Quelltext bearbeiten]Abweichende Notation
[Bearbeiten | Quelltext bearbeiten]Die Bezeichnung Beta-Fehler für den Fehler 2. Art ist in einigen Anwendungsbereichen (z. B. Biometrie, Medizin, Qualitätskontrolle) gebräuchlich, aber in der mathematischen Statistik weniger üblich. Die oben mit bezeichnete Gütefunktion, das ist die Wahrscheinlichkeit der Ablehnung der Nullhypothese in Abhängigkeit vom Parameter , wird in der mathematischen Statistik häufig mit bezeichnet.[13][14][15] In diesem Fall sind dann die Fehlerwahrscheinlichkeiten 2. Art durch für gegeben. Dies kann im Zusammenhang mit der Bezeichnung Beta-Fehler für eine Fehlerwahrscheinlichkeit 2. Art irritieren.
Interpretation der Fehlerwahrscheinlichkeiten als bedingte Wahrscheinlichkeiten
[Bearbeiten | Quelltext bearbeiten]Manchmal werden die Fehlerwahrscheinlichkeiten 1. und 2. Art als bedingte Wahrscheinlichkeiten bezeichnet.[1][16] Die Wahrscheinlichkeit ist die Wahrscheinlichkeit, dass die Nullhypothese abgelehnt wird, falls der Parameter vorliegt. Insoweit ist eine Wahrscheinlichkeit, die im umgangssprachlichen Sinn auf das Vorliegen des Parameters bedingt ist, da sich für jeden anderen Parameterwert eine andere Wahrscheinlichkeit ergeben kann. Es handelt sich also im umgangssprachlichen Sinn um eine bedingte Wahrscheinlichkeit, nicht aber im Sinn der Wahrscheinlichkeitstheorie, da kein Ereignis ist. In der Bayesschen Statistik wird ein Parameterwert als realisierter Wert einer Zufallsvariablen interpretiert. In dieser würde ein Ausdruck der Form Sinn als bedingte Wahrscheinlichkeit mit dem bedingenden Ereignis ergeben.
Simultane Kontrolle der Fehler 1. und 2. Art
[Bearbeiten | Quelltext bearbeiten]Es gibt Modifikationen des klassischen Neyman-Pearson-Ansatzes zur Testkonstruktion, bei denen die Null- und die Gegenhypothese symmetrisch behandelt werden, und die Fehler 1. und 2. Art simultan kontrolliert werden. Dies ist bei einer entscheidungstheoretischen Interpretation statistischer Test möglich, bei der die Fehler 1. und 2. Art durch eine Verlustfunktion bewertet werden.[17] In der klassischen Testtheorie gibt es die Konzepte des Alternativtests[18] – insbesondere des Niveau-α-β-Tests mit Indifferenzbereich[19] – und des so genannten agnostischen Tests[20], der neben einer Entscheidung für die Null- oder Gegenhypothese explizit einen Bereich ohne Entscheidung vorsieht.
Siehe auch
[Bearbeiten | Quelltext bearbeiten]Weblinks
[Bearbeiten | Quelltext bearbeiten]Literatur
[Bearbeiten | Quelltext bearbeiten]- Bernhard Rüger: Test- und Schätztheorie, Band II: Statistische Tests. Oldenbourg, München 2002, ISBN 3-486-25130-9.
- E. L. Lehmann, Joseph P. Romano: Testing Statistical Hypothesis. 4. Auflage. Springer, Cham 2022, ISBN 978-3-03070577-0, doi:10.1007/978-3-030-70578-7 (E-Book-ISBN 978-3-030-70578-7).
- Hermann Witting: Mathematische Statistik I. Parametrische Verfahren bei festem Stichprobenumfang. Teubner, Stuttgart 1985, ISBN 3-519-02026-2, Kap. 1.2, Kap. 2.
Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ a b Denes Szucs, John Ioannidis: When Null Hypothesis Significance Testing Is Unsuitable for Research: A Reassessment. In: Frontiers in human neuroscience, Band 11, 2017, S. 390, doi:10.3389/fnhum.2017.00390, PMID 28824397, PMC 5540883 (freier Volltext) (Review).
- ↑ Jerzy Neyman, Egon Pearson: On the Use and Interpretation of Certain Test Criteria for Purposes of Statistical Inference: Part I. In: Biometrika, Bd. 20A, Nr. 1/2 (Juli 1928), Oxford University Press, S. 175–240.
- ↑ Mit ist die Wahrscheinlichkeit des Ereignisses bezeichnet, die vom jeweiligen Parameter abhängt. Eine Interpretation als bedingte Wahrscheinlichkeit ist nicht intendiert. Übliche in der Literatur verwendete Bezeichnungen sind und . Im Rahmen der Bayesschen Statistik wird als realisierter Wert einer Zufallsvariablen interpretiert und damit wird eine Interpretation als bedingte Wahrscheinlichkeit möglich.
- ↑ a b Bernhard Rüger: Test- und Schätztheorie, Band II: Statistische Tests. 2002, S. 30.
- ↑ Hermann Witting: Mathematische Statistik I. Parametrische Verfahren bei festem Stichprobenumfang. Teubner, Stuttgart 1985, ISBN 3-519-02026-2, S. 36f.
- ↑ Hermann Witting: Mathematische Statistik I. Parametrische Verfahren bei festem Stichprobenumfang. Teubner, Stuttgart 1985, ISBN 3-519-02026-2, S. 42.
- ↑ George G. Judge, R. Carter Hill, W. Griffiths, Helmut Lütkepohl, T. C. Lee. Introduction to the Theory and Practice of Econometrics. 2. Auflage. John Wiley & Sons, New York / Chichester / Brisbane / Toronto / Singapore 1988, ISBN 0-471-62414-4, S. 96. ff
- ↑ James L. Johnson: Probability and Statistics for Computer Science. S. 340. ff
- ↑ Ludwig Fahrmeir, Rita Künstler, Iris Pigeot, Gerhard Tutz: Statistik. Der Weg zur Datenanalyse. 8., überarb. und erg. Auflage. Springer Spektrum, Berlin / Heidelberg 2016, ISBN 978-3-662-50371-3, S. 385.
- ↑ Bayer, Hackel: Wahrscheinlichkeitsrechnung und mathematische Statistik, S. 154
- ↑ George G. Judge, R. Carter Hill, W. Griffiths, Helmut Lütkepohl, T. C. Lee. Introduction to the Theory and Practice of Econometrics. 2. Auflage. John Wiley & Sons, New York / Chichester / Brisbane / Toronto / Singapore 1988, ISBN 0-471-62414-4, S. 96. ff
- ↑ Jeffrey Marc Wooldridge: Introductory econometrics: A modern approach. 4. Auflage. Nelson Education, 2015, S. 779.
- ↑ E. L. Lehmann, Joseph P. Romano: Testing Statistical Hypothesis. 2022, S. 62.
- ↑ Power of a statistical test. In: Encyclopedia of Mathematics. Abgerufen am 17. Februar 2023.
- ↑ Erwin Kreyszig: Statistische Methoden und ihre Anwendungen. 7. Auflage. Vandenhoeck und Ruprecht, Göttingen 1991, ISBN 978-3-525-40717-2, S. 209ff.
- ↑ Philipp Sibbertsen und Hartmut Lehne: Statistik: Einführung für Wirtschafts- und Sozialwissenschaftler., S. 379
- ↑ P. H. Müller (Hrsg.): Lexikon der Stochastik – Wahrscheinlichkeitsrechnung und mathematische Statistik. 5. Auflage. Akademie-Verlag, Berlin 1991, ISBN 978-3-05-500608-1, Entscheidungstheorie (statistische Entscheidungstheorie), S. 88–93.
- ↑ Bernhard Rüger: Test- und Schätztheorie, Band II: Statistische Tests. 2002, Abschnitt 3.3.1, S. 255–263.
- ↑ Bernhard Rüger: Test- und Schätztheorie, Band II: Statistische Tests. 2002, S. 248–263.
- ↑ Victor Coscrato, Rafael Izbicki, Rafael Bassi Stern: Agnostic tests can control the type I and type II errors simultaneously. In: Brazilian Journal of Probability and Statistics. Band 34, Nr. 2, 2020, S. 230–250, doi:10.1214/19-BJPS431.






































![{\displaystyle H_{0}:\theta \in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb437ade5c27769b55f9912b2a98c61c12143e3c)







