Gebundener Vektor
Als gebundener Vektor oder lokalisierter Vektor wird in der Technischen Mechanik ein Vektor bezeichnet, mit dem eine gerichtete physikalische Größe beschrieben wird, die einem bestimmten Punkt im Raum zugeordnet ist.[1][2][3][4] Ein Beispiel ist eine durch den Vektor gegebene Kraft, die auf einen Körper wirkt: je nach Angriffspunkt kann sie verschiedene Wirkungen haben. Wird ein gebundener Vektor durch einen Pfeil dargestellt, kann dieser nicht zu beliebigen Punkten im Raum verschoben werden, ohne dass sich die entsprechende physikalische Wirkung ändert.[5] Der gegenteilige Begriff freier Vektor gilt für vektorielle Größen, die unabhängig von jedem Bezugspunkt die gleiche Bedeutung haben. Ein Beispiel ist die Geschwindigkeit der Massenpunkte eines nur translatorisch bewegten starren Körpers, oder das Drehmoment eines Kräftepaars.
Der Begriff wurde von Heinrich Emil Timerding geprägt und auf einen an eine Wirkungslinie gebundenen Vektor bezogen, wie es etwa für die Kraft auf einen starren Körper im Fall des statischen Gleichgewichts gilt. August Föppl führte dafür später den Begriff linienflüchtiger Vektor ein.[6] In manchen älteren Lehrbüchern der Mechanik starrer Körper werden deswegen unter dem Begriff gebundener Vektor linienflüchtige Vektoren beschrieben, die entlang ihrer Wirkungslinie, aber nicht quer zu ihr, verschiebbar sind.[7]
Gebundene Vektoren werden vor allem in der Statik verwendet, um für ein System aus mehreren gleichzeitig wirkenden Kräften mit verschiedenen Richtungen und Angriffspunkten die Gesamtwirkung zu ermitteln. In Lehrbüchern der theoretischen Mechanik als Teilgebiet der Physik ist der Begriff ungebräuchlich.
Beschreibung[Bearbeiten | Quelltext bearbeiten]
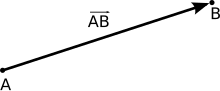
Ein an einen Punkt gebundener Vektor geht von einem festen Punkt A aus und wird durch Betrag und Richtung bestimmt. Durch den Betrag, der als Länge dargestellt wird, und die Richtung wird der Endpunkt B festgelegt. Ein gebundener Vektor wird entweder mit einem Buchstabenpaar bezeichnet, das den Anfangspunkt und den Endpunkt beschreibt und einem Pfeil, der beide Buchstaben überspannt; oder ein Einzelbuchstabe beschreibt den Namen des Vektors und wird als dieser Buchstabe überspannt mit einem Pfeil dargestellt:
- oder
Ein Spezialfall des gebundenen Vektors ist der Ortsvektor, der stets an den Koordinatenursprung gebunden ist und von null zu (hier) einem Punkt A zeigt.
- oder

Mathematisch kann ein gebundener Vektor durch das Symbol () dargestellt werden, das den Vektoranteil und den Ortsvektor des Bezugspunkts A angibt:[8]
- oder
Zwei gebundene Vektoren sind genau dann gleich, wenn sie denselben Vektoranteil und denselben Bezugspunkt haben. Beim Rechnen mit gebundenen Vektoren gelten für den Vektoranteil die üblichen Regeln der Vektoralgebra. Beispiele sind die Formeln für Massenmittelpunkt und Gesamtkraft im Schwerpunktsatz der Mechanik. Jedoch ist gesondert zu untersuchen, ob das Resultat wieder ein gebundener Vektor ist und welchen Bezugspunkt dieser gegebenenfalls hat. Durch welchen – gebundenen oder freien – Vektor ein System mehrerer gebundener Vektoren ersetzt werden darf, ist nach den Regeln für die zusätzlichen Begriffe Moment und Äquivalenz zu ermitteln.[9]
Das Moment eines gebundenen Vektors ist das Kreuzprodukt aus dem Ortsvektor seines Angriffspunkts und seinem Vektoranteil.
Momente gebundener Vektoren können vektoriell addiert werden, sofern sie denselben Bezugspunkt haben. Zwei Systeme gebundener Vektoren sind zueinander äquivalent (sprich gleichwertig), wenn sie unabhängig vom Bezugspunkt auf dasselbe resultierende Moment führen. Ein System gebundener Vektoren ist in seiner Wirkung äquivalent zu einem Paar gebundener Vektoren, das als Vektorwinder bezeichnet wird.[10][7]
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Statik-Skripte in maschinenbau-wissen.de
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Heinz Ulbrich, Hans-Jürgen Weidemann, Friedrich Pfeiffer: Technische Mechanik in Formeln, Aufgaben und Lösungen. Lehrbuch für den Maschinenbau. Springer, 2006, ISBN 3-8351-9058-X. (eingeschränkte Vorschau) (abgerufen am 8. April 2013)
- ↑ Lothar Papula: Papula, Mathematik 1. Ein Lehr- und Arbeitsbuch für das Grundstudium. Mit zahlreichen Beispielen aus Naturwissenschaft und Technik. Mit 307 Übungsaufgaben mit ausführlichen Lösungen. Springer, 2007, ISBN 978-3-8348-9220-1. (online, abgerufen am 9. April 2013)
- ↑ Akshay Ranjan Paul, Pijush Roy, Sachayan Mukherjee: Mechanical sciences : engineering mechanics and strength of materials. PHI Learning, 2004, ISBN 81-203-2611-3. (eingeschränkte Vorschau, englisch, abgerufen am 8. Mai 2013)
- ↑ V. P. Bhatnagar: A Complete Course in I.S.C. Physics. Vol I, 1997, ISBN 81-209-0385-4. (eingeschränkte Vorschau, englisch, abgerufen am 8. Mai 2013)
- ↑ James H. Allen: Statik für Maschinenbauer für Dummies. Verlag John Wiley & Sons, 2012, ISBN 978-3-527-70761-4. (eingeschränkte Vorschau, abgerufen am 9. April 2013)
- ↑ Waldemar Koestler, Moritz Tramer: Differential- und Integralrechnung: Infinitesimalrechnung für Ingenieure insbesondere auch zum Selbststudium. J. Springer, 1913, S. 70 (Fußnote)
- ↑ a b Kurt Meyberg, Peter Vachenauer: Höhere Mathematik, 1.Differential- und Integralrechnung, Vektor- und Matrizenrechnung. 6., korrigierte Auflage. Springer-Verlag, 2001, ISBN 3-642-56654-5. (eingeschränkte Vorschau)
- ↑ P. Eberhard, M, Hanss: Technische Mechanik 1. Systeme gebundener Vektoren, Institut für Technische und Numerische Mechanik (online ( des vom 22. September 2013 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis., PDF; 132 kB, abgerufen am 10. April 2013)
- ↑ Kurt Magnus, Hans Heinrich Müller-Slany: Grundlagen der technischen Mechanik. B. G. Teubner Verlag/ GWV Fachverlage, Wiesbaden 2005, ISBN 3-8351-0007-6 (eingeschränkte Vorschau in der Google-Buchsuche).
- ↑ Klaus Fritzsche: Mathematik 1 für Elektrotechnik und IT. Kapitel 2 Vektorrechnung. (Vorlesungsausarbeitung zum Wintersemester 2001/2002) (online)










