Drehmoment
| Physikalische Größe | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Name | Drehmoment | |||||||||
| Formelzeichen | ||||||||||
| ||||||||||

Das Drehmoment (auch Moment oder Kraftmoment, von lateinisch momentum Bewegungskraft[1]) ist eine physikalische Größe in der klassischen Mechanik, die die Drehwirkung einer Kraft, eines Kräftepaars oder sonstigen Kräftesystems auf einen Körper bezeichnet. Es spielt für Drehbewegungen die gleiche Rolle wie die Kraft für geradlinige Bewegungen. Ein Drehmoment kann die Rotation eines Körpers beschleunigen oder bremsen und den Körper verbiegen (Biegemoment) oder verwinden (Torsionsmoment). In Antriebswellen bestimmt das Drehmoment zusammen mit der Drehzahl die übertragene Leistung.
Die international verwendete Maßeinheit für das Drehmoment ist das Newtonmeter. Als Formelzeichen ist üblich.
Definition
[Bearbeiten | Quelltext bearbeiten]Hebel
[Bearbeiten | Quelltext bearbeiten]Wenn eine Kraft rechtwinklig auf den Arm eines Hebels der Länge wirkt, beträgt das Drehmoment:
Wenn die Kraft unter einem beliebigen Winkel angreift, gilt:
- .
Für (Kraft und Hebelarm parallel) ist der Sinus null: es tritt kein Drehmoment auf. Für ist der Sinus negativ: das Drehmoment wirkt in die entgegengesetzte Richtung.
Allgemein
[Bearbeiten | Quelltext bearbeiten]Generell ist das Drehmoment als vektorielles Kreuzprodukt definiert. Hierbei gibt die Richtung des Drehmomentvektors den Drehsinn des Drehmoments an.
Dabei ist der Verbindungsvektor vom Bezugspunkt des Drehmoments zum Angriffspunkt der Kraft. Dieser Bezugspunkt ist frei wählbar; es muss sich nicht um den Punkt handeln, um den sich der Körper dreht (ein solcher existiert teilweise nicht) und es muss auch nicht ein Punkt des Körpers sein, auf den die Kraft wirkt. Somit ist das Drehmoment einer einzelnen Kraft (wie auch der Drehimpuls) nur bezüglich eines Punktes definiert, der manchmal auch explizit angegeben wird:
- mit Bezugspunkt .
Wirken mehrere Kräfte () auf verschiedene Punkte ein, so ist das gesamte Drehmoment die Vektorsumme der einzelnen Drehmomente:
Wirken zwei parallele Kräfte auf einen Körper, die zwar denselben Betrag , aber entgegengesetzte Richtung haben, und deren Wirklinien einen gewissen Abstand haben, so verursachen sie ein Drehmoment mit dem Betrag . Man spricht dann von einem Kräftepaar.
Maßeinheit
[Bearbeiten | Quelltext bearbeiten]Die Maßeinheit des Drehmoments im SI ist das Newtonmeter (Nm). Mit den Basiseinheiten Kilogramm, Meter und Sekunde gilt:
Die Einheit der mechanischen Arbeit ist ebenfalls das Newtonmeter und hat den Namen „Joule“ (1 J = 1 N·m). Für das Drehmoment darf der Einheitenname „Joule“ aber nicht verwendet werden,[2] denn Drehmoment und Arbeit sind unterschiedliche physikalische Größen, die sich nicht ineinander umrechnen lassen. Arbeit wird erbracht, wenn bei einer Bewegung entlang einer Strecke eine Kraft(‑komponente) parallel zur Bewegung wirkt. Beim Drehmoment wirkt dagegen die Kraft senkrecht zu der durch den Hebelarm gebildeten Strecke. Die Arbeit ist eine skalare Größe, das Drehmoment hingegen ein Pseudovektor.
Dem Satz „Arbeit = Kraft mal Weg“ entspricht hier „Arbeit = Drehmoment mal Winkel“. Um diesen Zusammenhang darzustellen, kann für das Drehmoment als Energie pro Winkel auch die Einheit
verwendet werden.[2][3] Dabei ist die Maßeinheit Radiant für ebene Winkel.
In technischen Dokumenten und auf Typenschildern wird das Drehmoment in der Einheit Nm angegeben. Andere verwendete Einheiten sind z. B. oder Kombinationen aus anderen (Gewichts-)Kraft- und Längeneinheiten.
Bezeichnungen und Abgrenzung
[Bearbeiten | Quelltext bearbeiten]Drehmoment als Moment erster Ordnung
[Bearbeiten | Quelltext bearbeiten]Die Bezeichnung „Moment“ wird allgemein für Kenngrößen von Verteilungen benutzt, die sich auf die Form
bringen lassen.[4] Bei einem Drehmoment ist für das Maß die Funktion zu nehmen, die dem Ort eine Kraft zuordnet und die Ordnung zu wählen. Das Drehmoment ist daher das Moment erster Ordnung (Dipolmoment) einer Kraftverteilung.
Anstelle einer Kraftverteilung lassen sich auch andere physikalische Größen betrachten und deren Verteilungen, wie bei einer Multipolentwicklung, allgemein nach Momenten entwickeln. Die so entstehenden Größen, die keine Drehmomente sind, werden auch mit Wörtern bezeichnet, die die Endung ‑moment enthalten. Beispiele sind das Flächenmoment, das Trägheitsmoment oder das magnetische Moment.
Wortwahl in Naturwissenschaften und Technik
[Bearbeiten | Quelltext bearbeiten]In den Werken der theoretischen Mechanik und der Physik wird die hier behandelte physikalische Größe ganz allgemein als Drehmoment bezeichnet.[5] In der Technischen Mechanik sowie bei den DIN- und VDI-Normen wird die Größe meist allgemein als Moment bezeichnet. Selten wird es ebenfalls allgemein als Drehmoment bezeichnet,[6] teilweise wird die Bezeichnung Drehmoment auch als „umgangssprachlich“ abgelehnt.[7] Manchmal wird Drehmoment verwendet für das Moment eines Kräftepaares.[8][9] Meistens wird Drehmoment nur verwendet, wenn es zu einer Drehung des betrachteten Körpers kommt,[10] beispielsweise beim Festziehen von Schrauben oder bei Wellen von Motoren, aber nicht, wenn es zu einer Verformung kommt (Biege- oder Torsionsmoment) oder die Wirkung noch nicht bekannt ist (Moment).
In diesem Artikel wird im Folgenden die Bezeichnung Drehmoment im allgemeinen Sinne verwendet, gleichbedeutend mit dem Moment der Technischen Mechanik, und ist nicht beschränkt auf Drehbewegungen oder Kräftepaare.
Daneben gibt es noch eine Reihe von Drehmomenten, die mit der Nachsilbe ‑moment gebildet werden, wie das Biegemoment, das Torsionsmoment oder das Antriebsmoment. Bezeichnungen wie Biege-Drehmoment oder Torsions-Drehmoment kommen nicht vor.
Spezielle Drehmomente in der Technik
[Bearbeiten | Quelltext bearbeiten]Es wird unterschieden nach
Art der Beanspruchung:
- Biegemoment: Ein Moment, das ein Bauteil auf Biegung beansprucht.
- Torsionsmoment: Das Moment, das ein Bauteil auf Verdrehung (Torsion) beansprucht.
- Schnittmoment: Schnittreaktion beim Freischneiden.
Art der Bewegung:
- Gier-, Nick-, Wankmoment: Momente um spezielle Achsen eines starren Körpers beim Gieren, Nicken und Wanken.
Art der Wirkung:
- Anfahrmoment: Das Moment, das eine Kraftmaschine aus dem Stand leisten kann (seltener auch als Losbrechmoment bezeichnet) oder das eine Arbeitsmaschine oder ein Fahrzeug beim Anfahren benötigt.
- Antriebsmoment: Das Moment, das an der Eingangswelle einer Arbeitsmaschine oder eines Getriebes, an der Radachse eines Fahrzeugs oder an der Achse eines Propellers wirkt. Für die treibende Kraftmaschine oder das treibende Getriebe ist es das Abtriebsmoment.
- Anzugsdrehmoment oder Anziehdrehmoment: Das Moment, das beim Befestigen (Anziehen) einer Schraube aufgebracht wird.
- Kippmoment: In der Mechanik das Moment, das ein aufrecht stehendes Objekt umkippt. In der Elektrotechnik das maximale Moment in der Drehmoment/Drehzahl-Kennlinie eines Asynchronmotors. Für Details siehe Kipppunkt.
- Lastmoment: Das Moment, das eine Arbeitsmaschine der antreibenden Kraftmaschine oder dem Getriebe entgegensetzt. Für die Kraftmaschine oder das Getriebe ist es das Abtriebsmoment.
- Einspannmoment: Ein Moment, das erzeugt wird an der Einspannung, also der Befestigung eines Körpers. Es verhindert eine Drehung des Körpers.
- Versatzmoment: Moment einer Kraft bezüglich des Bezugspunkts für das Kräfte- und Momentengleichgewicht.
Sonstigem:
- Bemessungsmoment: Das Moment, für das ein Bauteil bei der Konstruktion bemessen wurde.
- Nennmoment: Das Moment, für das eine Komponente entworfen wurde.
- Spezifisches Drehmoment: Das Moment pro Liter Hubraum für Kolbenmotoren. Die Höchstwerte für Viertakt-Ottomotoren und für große Viertakt-Dieselmotoren liegen bei 200 Nm/dm³. Ganz große Zweitakt-Schiffsdiesel kommen auf 300 Nm/dm³.
Arten von Drehmomenten
[Bearbeiten | Quelltext bearbeiten]Es wird unterschieden zwischen
- dem Drehmoment einer einzelnen Kraft bezüglich eines Punktes,
- dem Drehmoment einer einzelnen Kraft bezüglich einer Achse und
- dem Drehmoment eines Kräftepaares.
Bei den ersten beiden Begriffen hängen Betrag und Drehsinn des Drehmomentes vom Bezugsstück (Punkt oder Gerade) ab. Beim Kräftepaar hingegen erhält man unabhängig vom Bezugsstück immer dasselbe Gesamtdrehmoment, wenn die Drehmomente der einzelnen Kräfte des Kräftepaares betrachtet und addiert werden.
Bei allen drei Arten sind zwei verschiedene gleichwertige Betrachtungsweisen möglich:
- Eine gemischte, geometrische und algebraische Betrachtung, bei der sich der Betrag des Drehmomentes ergibt als Produkt aus Kraft und Hebelarm. Die Wirkungsebene und der Drehsinn ergeben sich aus geometrischen Überlegungen.
- Die zweite Variante ist eine rein analytische. Das Drehmoment wird dabei als Vektor betrachtet, der sich als Vektorprodukt aus dem Verbindungsvektor und dem Kraftvektor ergibt. Der Drehmomentenvektor gibt dann den Betrag, die Wirkungsebene und den Drehsinn an.
Welche Betrachtung zweckmäßiger ist, hängt von der zu untersuchenden Problemstellung und von den mathematischen Kenntnissen des Anwenders ab. Falls alle wirkenden Kräfte in derselben Ebene liegen, bietet sich die geometrisch-algebraische Betrachtung an, die mit einer vergleichsweise einfachen Mathematik auskommt. Bilden die Kräfte ein räumliches Kraftsystem, ist ein derartiges Vorgehen zwar möglich, aber schwierig. Die vektorielle Darstellung bietet sich dann an, erfordert aber Kenntnisse von fortgeschritteneren Konzepten der Mathematik wie dem Vektorprodukt. Außerdem sind allgemeine mathematische Beziehungen zwischen dem Drehmoment und anderen physikalischen Größen, wie sie in der Theoretischen Mechanik untersucht werden, leichter mit Vektoren darstellbar. In Schulbüchern und einführenden Lehrbüchern[11][12] der Technischen Mechanik wird zunächst die geometrisch-algebraische Betrachtung bevorzugt. In Lehrbüchern zur Theoretischen Mechanik[13] und Nachschlagewerken[14] zur Technischen Mechanik ist dagegen die vektorielle Darstellung verbreitet.
Bei allen drei Arten gilt für den Betrag des Drehmomentes: Kraft mal Hebelarm. Ein einzelnes Drehmoment wirkt in einer Ebene und es ist grundsätzlich ausreichend, diese Ebene zu betrachten. Das Drehmoment kann dann durch eine einzelne Zahl angegeben werden, deren Vorzeichen den Drehsinn angibt. Drehmomente die gegen den Uhrzeigersinn drehen, also im mathematisch positiven Sinn, werden meist positiv gezählt. Bei mehreren Drehmomenten, die nicht in derselben Ebene wirken, ist es zweckmäßiger, sie mit ihrem Drehmomentenvektor zu beschreiben. Dieser steht senkrecht auf der Ebene, in der das Drehmoment wirkt.
Zur theoretischen Herleitung der Drehmomente sind verschiedene Wege möglich. Ausgehend von den Grundgesetzen der Mechanik kann das Drehmoment einer einzelnen Kraft definiert werden. Das Drehmoment eines Kräftepaares ergibt sich dann als Summe der Drehmomente der beiden Kräfte. Stattdessen führen Überlegungen zur Resultierenden eines Kräftepaares direkt auf sein Drehmoment. Das Drehmoment einer einzelnen Kraft ergibt sich dann durch die Verschiebung der Kraft auf eine parallele Wirkungslinie (Versatzmoment, siehe weiter unten Verschiebung von Kräften).
Drehmoment einer Kraft bezüglich eines Punktes
[Bearbeiten | Quelltext bearbeiten]
Das Drehmoment oder Moment einer (einzelnen) Kraft bezüglich eines Punktes wirkt in der Ebene, die die Kraft und den Bezugspunkt enthält. In dieser Ebene ist sein Betrag definiert als Produkt aus dem Hebelarm und dem Betrag der Kraft :
Um Verwechslungen mit anderen Drehmomenten zu vermeiden, wird der Bezugspunkt auch notiert:
- oder .
Der Hebelarm ist der senkrechte Abstand zwischen dem Bezugspunkt und der Wirkungslinie der Kraft. Diese ist im Allgemeinen nicht die direkte Verbindungslinie zwischen dem Bezugspunkt und dem Angriffspunkt der Kraft. Da sich der Hebelarm nicht ändert, wenn die Kraft entlang ihrer Wirkungslinie verschoben wird, ändert sich dabei auch nicht ihr Drehmoment. Der Bezugspunkt selbst ist frei wählbar. Es muss sich nicht um den Punkt handeln, um den sich der betrachtete Körper dreht. Dieser ist teilweise nicht bekannt und bei Körpern, die fest mit ihrer Umgebung verbunden sind, gibt es einen solchen Punkt gar nicht. Der Bezugspunkt muss auch nicht Teil des Körpers sein, auf den die Kraft wirkt. Sowohl der Betrag als auch der Drehsinn des Drehmomentes hängt von der Wahl des Bezugspunktes ab.
Die vektorielle Definition lautet
- .
Es handelt sich um das Vektorprodukt aus dem Verbindungsvektor , der vom Bezugspunkt zum Angriffspunkt der Kraft zeigt und dem Kraftvektor . Der Betrag des Verbindungsvektors entspricht im Allgemeinen nicht dem Hebelarm. Der Betrag des Drehmomentenvektors lässt sich berechnen aus den Beträgen des Verbindungs- und Kraftvektors und dem Winkel zwischen beiden zu
Es gilt somit .
Häufig wird das Drehmoment auch per Konvention immer auf den Ursprung bezogen:
Der Verbindungsvektor ist dann der Ortsvektor des Angriffspunkts der Kraft.
Der Drehmomentenvektor steht senkrecht auf der Ebene, in der das Drehmoment wirkt, und damit auch senkrecht auf der Ebene, die durch den Kraft- und Verbindungsvektor aufgespannt wird. Sein Betrag, also seine Länge, entspricht dem Betrag des Drehmomentes und dem Flächeninhalt des Parallelogramms, das durch den Verbindungs- und Kraftvektor gebildet wird. Der Drehsinn ergibt sich durch die Rechte-Hand-Regel: Wenn man den Drehmomentenvektor in Gedanken mit der rechten Hand derart umfasst, dass der Daumen in Richtung der Pfeilspitze zeigt, dann geben die übrigen Finger den Drehsinn an.
Drehmoment einer Kraft bezüglich einer Achse
[Bearbeiten | Quelltext bearbeiten]Beim Drehmoment einer Kraft bezüglich einer Achse wird als Bezugspunkt der Punkt der Achse gewählt, der dem Angriffspunkt der Kraft am nächsten liegt. Der Abstand des Angriffspunkts von der Achse ist dann der Hebelarm. Zur Berechnung kann man die Kraft in eine Ebene projizieren, die senkrecht zur Achse steht, und dann von der projizierten Kraft das Drehmoment bezüglich des Punktes bilden, in dem die Achse die Ebene durchstößt.[15] Alternativ[16] kann auch das Drehmoment der ursprünglichen Kraft bezüglich eines beliebigen Punktes auf der Geraden gebildet werden. Anschließend wird der Drehmomentenvektor auf die Gerade projiziert.
Drehmoment eines Kräftepaares
[Bearbeiten | Quelltext bearbeiten]
Ein Kräftepaar besteht aus zwei Kräften, die sich auf parallelen Wirkungslinien befinden, den gleichen Betrag haben und in entgegengesetzte Richtungen zeigen. Im Gegensatz zu einer einzelnen Kraft kann es einen Körper nicht verschieben, aber es versucht ihn zu drehen. Kräftepaare sind häufig vorhanden, wenn es zu einer Drehbewegung von Körpern kommt; eine der beiden Kräfte ist aber häufig nicht sofort zu erkennen, weil es sich meist um eine Zwangskraft handelt.[17] Der Betrag des Drehmomentes, das von einem Kräftepaar erzeugt wird, lässt sich berechnen als Produkt aus dem Betrag einer der beiden Kräfte und dem Abstand ihrer Wirkungslinien:[18][19]
Der Drehmomentenvektor des Kräftepaares lässt sich berechnen durch:
Der Verbindungsvektor zeigt von einem beliebigen Punkt auf der Wirkungslinie der einen Kraft zu einem beliebigen Punkt auf der Wirkungslinie der anderen Kraft. Häufig wird der Vektor genutzt, der die Angriffspunkte der beiden Kräfte verbindet.
Die Wirkung von Kräftepaaren unterscheidet sich in einigen wichtigen Punkten von einzelnen Kräften, weshalb die Drehmomente von Kräftepaaren sich ebenfalls von anderen Drehmomenten unterscheiden:
- Das Drehmoment eines Kräftepaares ist unabhängig von Bezugspunkten. Dies bedeutet, dass ein Kräftepaar an jeden beliebigen Ort verschoben werden kann, ohne dass sich seine Wirkung oder sein Drehmoment ändert.
- Ein Kräftepaar kann durch sein Drehmoment ersetzt werden, ohne dass sich die Wirkung auf den Körper, auf den es wirkt, ändert. Eine einzelne Kraft kann dagegen nicht durch ihr Drehmoment ersetzt werden.
- Der Drehmomentenvektor eines Kräftepaares kann an jeden beliebigen Ort verschoben werden. Es handelt sich um einen freien Vektor. Der Drehmomentenvektor einer Kraft ist dagegen ein axialer Vektor. Er kann nur entlang der Geraden verschoben werden, die er festlegt.
Herleitungen und Beziehungen zwischen den Drehmomentarten
[Bearbeiten | Quelltext bearbeiten]Es gibt verschiedene Möglichkeiten, die Drehmomente ausgehend von den Grundgesetzen der Mechanik herzuleiten.
- In der Theoretischen Mechanik
In der Theoretischen Mechanik gibt es mehrere Wege zur Herleitung des Drehmoments. Zum Beispiel kann man vom zweiten Newtonschen Gesetz
ausgehen. Durch vektorielle Multiplikation von links mit erhält man hieraus
- .
Auf der linken Seite steht das Drehmoment und auf der rechten Seite die zeitliche Ableitung des Drehimpulses, also ist
- .
Das Drehmoment eines Kräftepaares ergibt sich aus der Addition der Drehmomente der beiden Kräfte:
Da im Kräftepaar gilt, folgt auch
- ,
in Übereinstimmung mit der obigen Definition des Drehmoments eines Kräftepaars, denn .
- In der Technischen Mechanik
In der Technischen Mechanik führen Überlegungen zur Resultierenden von Kräftesystemen direkt zum Drehmoment eines Kräftepaares. Daraus lässt sich das Drehmoment einer einzelnen Kraft herleiten.
Mit dem Kräfteparallelogramm lassen sich zwei Kräfte mit gemeinsamem Angriffspunkt durch eine resultierende Kraft ersetzen. Wenn die beiden Kräfte auf einen starren Körper wirken, können sie auch zusammengefasst werden, wenn sich nur die Wirkungslinien der beiden Kräfte schneiden, da die Kräfte dann zum Schnittpunkt verschoben werden können, ohne dass sich die Wirkung auf den Körper ändert. Bei parallelen Kräften gibt es aber keinen Schnittpunkt. Falls die beiden Kräfte ungleiche Stärke haben, kann aber ein Schnittpunkt gefunden und eine resultierende Kraft gebildet werden durch Hinzufügen zweier weiterer Kräfte, deren resultierende Kraft null ist. Für das Kräftepaar ergibt sich jedoch dabei kein Schnittpunkt, sondern ein anderes Kräftepaar, möglicherweise an einem anderen Ort und mit gedrehten Wirkungslinien in anderem Abstand voneinander und veränderter Stärke der beiden entgegengesetzt gleichen Kräfte. Dabei bleibt das Produkt Kraft mal Abstand der Wirkungslinien, also das Drehmoment, immer konstant. Das Kräftepaar kann nicht durch eine einzelne resultierende Kraft ersetzt werden, sondern nur durch ein anderes Kräftepaar mit gleichem Drehmoment. Das Kräftepaar kann daher ganz allgemein durch sein Drehmoment ersetzt werden.
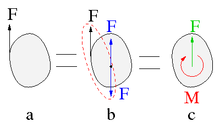
Das Drehmoment einer einzelnen Kraft bezüglich eines Punktes ergibt sich aus dem Drehmoment eines Kräftepaares unter Verwendung des Versetzungsmoments (siehe weiter unten Verschiebung von Kräften). Man betrachtet die zur Wirkungslinie parallele Linie durch den Bezugspunkt als Wirkungslinie von zwei hinzugefügten entgegensetzt gleichen Kräften derselben Größe wie die Einzelkraft. Die Einzelkraft wird mit der entsprechenden neuen Kraft zu einem Kräftepaar zusammengefasst und dieses dann durch sein Drehmoment ersetzt. Das Ergebnis entspricht der Versetzung der ursprünglichen Einzelkraft und dem Hinzufügen des Drehmomentes eines Kräftepaares. Letzteres ist das Versatzmoment.
Darstellungen und Notationen
[Bearbeiten | Quelltext bearbeiten]Für Drehmomente gibt es zahlreiche Notationen in Gleichungen und Darstellungen in Zeichnungen. Wird in Zeichnungen eine Ebene dargestellt, in der das Drehmoment wirkt, dann wird es meist durch einen gebogenen Pfeil dargestellt, der zwischen einem Viertelkreis und einem Dreiviertelkreis reichen kann. Die Spitze gibt dann den Drehsinn an. In dreidimensionalen Darstellungen werden Pfeile als Dreiviertelkreis genutzt, die um bestimmte Achsen drehen oder gerade Pfeile, die die Drehmomentenvektoren anzeigen. Diese können, wie bei Vektoren allgemein üblich, durch einen einfachen Pfeil dargestellt werden. Da bei vielen Problemstellungen in der Mechanik Kräfte und Drehmomente gleichzeitig vorkommen, werden zur Vermeidung von Verwechslungen die Drehmomentenvektoren auch mit einer Doppelspitze gekennzeichnet.[20]
Abhängigkeit vom Bezugspunkt
[Bearbeiten | Quelltext bearbeiten]Bei Systemen, die nicht im Gleichgewicht sind, ist der Wert des Drehmomentes im Allgemeinen abhängig von der Wahl des Bezugspunktes. Wird der Bezugspunkt um die Strecke verschoben, so hat das Drehmoment bezüglich des neuen Bezugspunktes den Wert
Dabei ist die resultierende Kraft, d. h. die Summe aller einzelnen Kräfte .
Ist die resultierende Kraft gleich null, so erfährt der Körper keine Beschleunigung und der Schwerpunkt ändert nicht seine Geschwindigkeit oder Bewegungsrichtung. Die Kraft bewirkt ausschließlich eine Änderung des Drehimpulses. In diesem Fall ist das Drehmoment unabhängig von seinem Bezugspunkt und kann frei verschoben werden, ohne die Wirkung auf die Körper zu verändern.[21] Da für diese Situation (mindestens) zwei Kräfte nötig sind, die denselben Betrag , aber eine entgegengesetzte Richtung, und deren Wirklinien einen gewissen Abstand haben, spricht man von einem Kräftepaar. Das Kräftepaar verursacht ein Drehmoment mit dem Betrag .
Addition von Drehmomenten
[Bearbeiten | Quelltext bearbeiten]Drehmomente können addiert werden zu einem resultierenden Drehmoment, ähnlich wie Kräfte zu einer resultierenden Kraft addiert werden können. Wenn sämtliche Drehmomente berücksichtigt werden, spricht man auch vom Gesamtdrehmoment. Zusammenhänge zwischen der resultierenden Kraft und dem resultierenden Drehmoment macht der Momentensatz.
Gesamtdrehmoment
[Bearbeiten | Quelltext bearbeiten]Die einzelnen Drehmomente zweier Kräfte können addiert werden, wenn sie sich auf denselben Punkt beziehen:
Wenn beliebig viele Kräfte () vorhanden sind, so ist das Gesamtdrehmoment die Summe über alle Drehmomente. Wenn sie auf den Ursprung bezogen werden, ergibt sich
- .
Der Vektor zeigt dabei vom Ursprung zum Fußpunkt der Kraft . Falls Kräftepaare durch ihre Drehmomente ersetzt wurden, müssen diese zusätzlich addiert werden:
Momentensatz der Statik
[Bearbeiten | Quelltext bearbeiten]Der Momentensatz der Statik besagt, dass das Moment der resultierenden Kraft auf einen Körper dieselbe Wirkung hat wie das Gesamtmoment, das sich aus der Summe der einzelnen Momente ergibt:
Die resultierende Kraft, die aus allen vorhandenen Kräften gebildet wird, muss dieselbe Wirkung auf einen Körper haben wie die Wirkungen der einzelnen Kräfte zusammen genommen. Aus der Vektoraddition der einzelnen Kräfte ergeben sich zwar Betrag und Richtung der resultierenden Kraft, aber weder ihr Angriffspunkt noch ihre Wirkungslinie. Diese werden mithilfe des Momentensatzes bestimmt. Die resultierende Kraft muss auf derjenigen Wirkungslinie liegen, auf der sie dasselbe Moment erzeugt wie die Momente der einzelnen Kräfte zusammen genommen.
Bedeutung hat der Momentensatz vor allem bei der Überprüfung des Momentengleichgewichtes oder für die Berechnung unbekannter Kräfte mithilfe des Momentengleichgewichtes. Kräfte, die schräg zu den Koordinatenachsen im Raum liegen, können dann aufgespalten werden in mehrere Kräfte, die senkrecht auf den Achsen stehen. Deren Momente lassen sich einfacher berechnen. Die von diesen Kraftkomponenten bewirkten Momente entsprechen in Summe dem Moment, das durch die ursprüngliche Kraft bewirkt wird.
Gleichgewicht
[Bearbeiten | Quelltext bearbeiten]Wenn sich ein Körper im mechanischen Gleichgewicht befindet, dann ändert er seinen Bewegungszustand nicht. Er wird also weder beschleunigt noch abgebremst.
Befindet sich ein Körper im Gleichgewicht, so befindet er sich sowohl im Kräftegleichgewicht, als auch im Drehmomentengleichgewicht oder Momentengleichgewicht bezüglich eines beliebigen Punktes :
Dies gilt für jeden beliebigen Punkt und damit sogar für Punkte, die außerhalb des Körpers liegen. Es bietet sich ein Punkt an, an dem sich die Wirkungslinien möglichst vieler Kräfte schneiden. Bei diesen ist die Länge des Hebelarms null, was zu einem Drehmoment von null führt. Diese Drehmomente tauchen folglich in der Gleichung nicht auf, was die Berechnung erleichtert. Wenn sich unter diesen Kräften nur eine einzige unbekannte Kraft befindet, so kann man diese unmittelbar berechnen. Manchmal kann es günstig sein, mehrere Drehmomentengleichgewichte zu bestimmen, wenn sich dadurch jeweils eine andere unbekannte Kraft berechnen lässt.
Wenn sich ein Körper im Drehmomentengleichgewicht bezüglich eines Punktes befindet, so kann man daraus nicht schließen, dass er sich auch insgesamt im Gleichgewicht befindet und ebenso wenig, dass er sich bezüglich anderer Punkte im Drehmomentengleichgewicht befindet. Wenn beispielsweise nur eine einzige Kraft wirkt, so befindet er sich im Drehmomentengleichgewicht bezüglich eines Punktes auf der Wirkungslinie dieser Kraft, aber bezüglich Punkten abseits dieser Linie nicht im Drehmomentengleichgewicht und auch nicht insgesamt im Gleichgewicht, da ja eine Kraft wirkt, für die es keine Gegenkraft gibt. Ein Körper befindet sich jedoch innerhalb einer Ebene insgesamt im Gleichgewicht, wenn er sich bezüglich drei verschiedener Punkte im Drehmomentengleichgewicht befindet, sofern diese drei Punkte nicht auf einer Geraden liegen.[22]
Verschiebung von Kräften
[Bearbeiten | Quelltext bearbeiten]Ein Kraftpfeil darf entlang seiner Wirkungslinie ohne Einschränkung verschoben werden, ohne dabei seine Wirkung auf einen starren Körper zu verändern. In der Position, wo der Abstandsvektor senkrecht zur Wirkungslinie des Kraftpfeils steht, wird er als Hebelarm bezeichnet. Betragsmäßig gilt dann: „Drehmoment gleich Hebelarm mal Kraft“. Bei zwei angreifenden Kräften (die dann als Kraft und Last bezeichnet werden) ist das Drehmomentengleichgewicht äquivalent zum Hebelgesetz:
- Kraftarm mal Kraft = Lastarm mal Last.
(Man beachte, dass streng genommen nur die Beträge gleich sind, denn die beiden Drehmomente sind gegensinnig und haben daher unterschiedliche Vorzeichen.)
Wird eine Kraft senkrecht zu ihrer Wirkungslinie um den Abstand verschoben auf eine parallele Wirkungslinie, so ändert sich das von ihr verursachte Drehmoment gegenüber dem Bezugspunkt. Eine Kraft darf folglich nur dann derart verschoben werden, wenn zusätzlich ein Drehmoment eingeführt wird, das diese Änderung wieder ausgleicht. Dieses wird als Versetzungsmoment[23][24] oder Versatzmoment[25] bezeichnet und hat den Betrag .
Dynamik
[Bearbeiten | Quelltext bearbeiten]Die Dynamik beschäftigt sich mit Zuständen, die sich nicht im Gleichgewicht befinden. Nach dem 2. Newtonschen Gesetz führt eine resultierende äußere Kraft an einem Körper zu einer Geschwindigkeitsänderung (Beschleunigung). Analog dazu bedeutet ein resultierendes äußeres Drehmoment eine Änderung der Winkelgeschwindigkeit (Winkelbeschleunigung ). Drehmomente im Inneren des Körpers (Biege- oder Torsionsmoment) spielen keine Rolle für die Bewegungsänderung. Das Trägheitsverhalten bezüglich der Rotation hängt nicht nur von der Masse eines Körpers, sondern auch von deren räumlicher Verteilung ab. Dies wird durch das Trägheitsmoment ausgedrückt. Bei einer Drehung um eine feste Achse gilt für das Drehmoment in Richtung dieser Achse:
Hierbei ist zu beachten, dass das Trägheitsmoment nicht nur von der Position der Drehachse (siehe Steinerscher Satz), sondern auch von ihrer Richtung abhängig ist. Will man die obige Gleichung allgemeiner für jede beliebige Raumrichtung formulieren, so muss man stattdessen den Trägheitstensor verwenden:

Man kann den Zusammenhang von Drehmoment und Änderungsrate des Drehimpulses (, Drall, Impulsmoment) ausdrücken als:
Diese Gleichung wird in der Technischen Mechanik als Drallsatz,[26] Drehimpulssatz,[27] Momentensatz[27] oder Impulsmomentsatz[28] bezeichnet. (Drehimpulssatz steht auch für den Drehimpuls-Erhaltungssatz, Momentensatz steht auch für den Momentensatz aus der Statik.)
Im zweidimensionalen Spezialfall bewirkt ein Drehmoment lediglich eine Beschleunigung oder Abbremsung einer Rotationsbewegung. Im allgemeinen dreidimensionalen Fall kann es hingegen auch die Richtung der Rotationsachse verändern (siehe z. B.: Präzession).
Entsprechungen zwischen geradliniger Bewegung und Drehbewegung
[Bearbeiten | Quelltext bearbeiten]Das Drehmoment nimmt in der klassischen Mechanik für Drehbewegungen eine ähnliche Rolle ein wie die Kraft für geradlinige Bewegungen:
| Geradlinige Bewegung | Drehbewegung | |
|---|---|---|
| Arbeit | Kraft mal Weg [A 1] |
Drehmoment mal Drehwinkel (Bogenmaß) [A 1] |
| allgemein: |
allgemein: | |
| Leistung | Kraft mal Geschwindigkeit |
Drehmoment mal Winkelgeschwindigkeit |
| Statisches Gleichgewicht | Kräftegleichgewicht |
Drehmomentengleichgewicht |
| Beschleunigte Bewegung | Masse mal Beschleunigung |
Trägheitstensor mal Winkelbeschleunigung |
| Änderungsrate des Impulses |
Änderungsrate des Drehimpulses |
- ↑ a b Diese vereinfachten Formeln gelten für eine konstante Kraft entlang eines Weges in Kraftrichtung beziehungsweise ein konstantes Drehmoment um eine Achse in Drehrichtung. Bei veränderlichen Kräften und Drehmomenten oder bei schiefwinkligen Anordnungen sind die allgemeinen Formeln in der Zeile darunter zu verwenden.
Messung des Drehmoments
[Bearbeiten | Quelltext bearbeiten]Ruhender Körper
[Bearbeiten | Quelltext bearbeiten]Der drehbare Körper wird durch ein statisches Gegenmoment in Ruhe gehalten. Das auf den ruhenden Körper wirkende und zu messende Drehmoment ist gleich groß wie das Gegenmoment, das zum Beispiel mit einem Hebel erzeugt wird, und dessen Wert das Produkt aus der Hebelarmlänge und der Gegenkraft am Hebelende ist.
Drehender Körper
[Bearbeiten | Quelltext bearbeiten]Das an einer rotierenden Welle bei bestimmter Drehzahl wirkende Drehmoment wird mit einem Bremsdynamometer, zum Beispiel einem Pronyschen Zaum oder einer Wasserwirbelbremse, gemessen. Diese an die Welle angeschlossene Bremseinrichtung nimmt die gesamte übertragene Leistung auf und misst gleichzeitig das Drehmoment.
Zum Beispiel eine Kraftmaschine, an deren Welle das Drehmoment zu messen ist, oder die Bremseinrichtung werden drehbar um die Rotationsachse der Welle gelagert und am freien Ende eines an der Maschine oder an der Bremseinrichtung befestigten Hebelarms die gegenwirkende Umfangskraft gemessen.
Die Messung wird mehrmals wiederholt und eine Drehmoment/Drehzahl-Kennlinie erzeugt.
Das die Drehgeschwindigkeit verändernde Drehmoment lässt sich durch Messen der Winkelbeschleunigung bestimmen, wenn das Trägheitsmoment bekannt ist. Die Auswertung erfolgt mit der Formel
- .
Drehmomente an ausgewählten Maschinen
[Bearbeiten | Quelltext bearbeiten]Elektromotoren
[Bearbeiten | Quelltext bearbeiten]
Obere Kennlinie: Dreieckschaltung
Mittlere Kennlinie: Sternschaltung
Der Asynchronmotor in der Ausführung als Kurzschlussläufer ist ein häufig verwendeter Elektromotor. Das Bild zeigt das bei Betrieb am Stromnetz (Frequenz und Spannung konstant) typisch erzeugte Drehmoment in Abhängigkeit von der Drehzahl. Der Motor kann über längere Zeit nur in dem kleinen Drehzahlbereich rechts von den Kipppunkten K1 oder K2 auf der steil abfallenden Kurve betrieben werden. Links von den Kipppunkten ist der Anlaufbereich, der immer möglichst schnell durchfahren werden muss. Beim Anlauf hat der Asynchronmotor einen schlechten Wirkungsgrad, einen hohen Anlaufstrom und ein geringes Drehmoment. Um diese Nachteile zu vermeiden, wendet man verschiedene Maßnahmen an, zum Beispiel die Stern-Dreieck-Anlaufschaltung oder den Betrieb an einem Frequenzumrichter. Mittels letzterem gelingt der Anlauf mit mehr als dem Nennmoment, sodass der Motor auch bei Fahrzeugantrieben eingesetzt werden kann.
Ein ebenfalls häufig verwendeter Motor ist der Reihenschluss-Gleichstrommotor, der ein besonders hohes Anlaufmoment hat. Er wird daher für Handgeräte, Waschmaschinen oder auch Bahnantriebe genutzt.
Verbrennungsmotoren
[Bearbeiten | Quelltext bearbeiten]
In Automobilprospekten ist es üblich, bei Verbrennungsmotoren anstatt der im Volllastbetrieb aufgenommenen Drehmoment/Drehzahl-Kennlinie (siehe Abbildung „Kennlinien zweier Verbrennungsmotoren“) nur deren Maximalwert gemeinsam mit der entsprechenden Drehzahl anzugeben.[29]
Da in der Gleichung für die Leistung die Drehzahl nochmals als linearer Faktor enthalten ist, liegt das Maximum der Leistung bei einer höheren Drehzahl als das Maximum des Drehmoments (siehe Abbildung).
Für das Drehmoment von Zweitaktmotoren gilt die Formel:
Hierbei ist das Hubvolumen und der Mitteldruck des verbrannten Treibstoffs, also die in dem Zyklus erbrachte Arbeit als „Kraft mal Weg“.
Für das Drehmoment von Viertaktmotoren gilt entsprechend:
Denn bei zwei Umdrehungen pro Arbeitszyklus halbiert sich die Arbeit pro Umdrehung gegenüber dem Zweitakter.
- Zahlenbeispiel
- Drehmoment und Leistung eines Viertaktmotors
Ein Serienfahrzeug mit 2000 cm³ (= 0,002 m³) Hubvolumen, dessen Viertaktmotor bei einer Drehzahl von 2000/min einen Mitteldruck von 9 bar (= 900.000 Pa; 1 Pa = 1 N/m²) erreicht, in SI-Einheiten gerechnet:
Die Gleichung für die Leistung bei einer Drehbewegung lautet (siehe oben; … Drehzahl, Anzahl der Umdrehungen pro Zeitspanne)
und als Funktion der Drehzahl
- .
ist die für einen bestimmten Motor drehzahlabhängige Drehmomentkennlinie. Sie wird durch Messung erhalten.
Ein Verbrennungsmotor, der bei Drehzahl 2000 Umdrehungen pro Minute das Drehmoment 143 Nm abgibt, hat in diesem Betriebszustand folgende Leistung:
- .
Hydraulikmotoren
[Bearbeiten | Quelltext bearbeiten]Die hydraulische Leistung eines Hydraulikmotors errechnet sich aus den Drücken und am Motoreingang oder -ausgang und dem geschluckten Ölvolumen ( ist das Volumen je Umdrehung):
Aus der Gleichung für die Leistung bei einer Drehbewegung (siehe oben)
folgt das Drehmoment zu:
Literatur
[Bearbeiten | Quelltext bearbeiten]- Wolfgang Nolting: Klassische Mechanik. In: Grundkurs Theoretische Physik. Bd. 1, 8. Auflage. Springer, Berlin 2008, ISBN 978-3-540-34832-0.
- Herbert Goldstein, Charles P. Poole und John L. Safko: Klassische Mechanik (Übersetzung: Michael Baer). 3., vollst. überarb. und erw. Auflage. Wiley-VCH, Weinheim 2006. (Lehrbuch Physik), ISBN 3-527-40589-5.
- Richard P. Feynman: Feynman-Vorlesungen über Physik. Oldenbourg, München/Wien 2007, ISBN 978-3-486-58444-8.
- Paul A. Tipler: Physik. 3. korrigierter Nachdruck der 1. Auflage. 1994, Spektrum Akademischer Verlag, Heidelberg/Berlin 2000, ISBN 3-86025-122-8.
- Ludwig Bergmann, Clemens Schaefer: Mechanik – Akustik – Wärme. In: Lehrbuch der Experimentalphysik. Bd. 1, 12. Auflage. Walter de Gruyter, Berlin 2008, ISBN 978-3-11-019311-4.
- Istvan Szabó: Einführung in die Technische Mechanik. Springer, Berlin 1999, ISBN 3-540-44248-0.
- Peter Gummert, Karl-August Reckling: Mechanik. Vieweg, Wiesbaden 1994, ISBN 3-528-28904-X.
Weblinks
[Bearbeiten | Quelltext bearbeiten]- Drehmoment am einarmigen Hebel. Dargestellt am Beispiel eines Schraubenschlüssels. Bei: zum.de.
- Wilfried Krimmel: Entwicklung und Zukunft der Drehmomentmesstechnik. Bei: lorenz-messtechnik.de.
Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ Das Online-Wörterbuch. In: de.pons.com. PONS GmbH, abgerufen am 23. April 2017.
- ↑ a b „Even though torque has the same dimension as energy (SI unit joule), the joule is never used for expressing torque.“ The International System of Units (SI) 9. edition, 2019, Kap. 2.3.4, Seite 140
- ↑ Das Internationale Einheitensystem (SI). Deutsche Übersetzung der BIPM-Broschüre „Le Système international d’unités/The International System of Units (8e édition, 2006)“. In: PTB-Mitteilungen. Band 117, Nr. 2, 2007, S. 21 (Online [PDF; 1,4 MB]).
- ↑ Palle E. T. Jørgensen, Keri A. Kornelson, Karen L. Shuman: Iterated Function Systems, Moments, and Transformations of Infinite Matrices. In: Memoirs of the American Mathematical Society. American Mathematical Society, 2011, ISBN 0-8218-8248-1, S. 2 (eingeschränkte Vorschau in der Google-Buchsuche).
- ↑ Elektronische Stichwortsuche in:
- Bartelmann, Feuerbacher, Krüger, Lüst, Rebhan, Wipf (Hrsg.): Theoretische Physik. Springer, 2015.
- Achim Feldmeier: Theoretische Mechanik – Analysis der Bewegung. 2013.
- Honerkamp, Römer: Klassische Theoretische Physik. Springer, 4. Auflage, 2012.
- Wolfgang Nolting: Grundkurs Theoretische Mechanik 1 – Klassische Mechanik. Springer, 10. Auflage, 2013.
- Norbert Straumann: Theoretische Mechanik. Springer, 2. Auflage, 2015.
- ↑ Böge, Böge: Technische Mechanik. Springer, 31. Auflage, 2015, S. 4.
- ↑ Spura: Technische Mechanik 1 – Stereostatik. Springer, 2016, S. 43.
- ↑ Böge: Handbuch Maschinenbau. Springer, 21. Auflage, 2013, S. C2.
- ↑ Mahnken: Lehrbuch der Technischen Mechanik – Statik. Springer, 2012, S. 98.
- ↑ Elektronische Stichwortsuche in:
- Dankert, Dankert: Technische Mechanik. Springer, 7. Auflage, 2013.
- Wittenburg u. a. (Hrsg.): Das Ingenieurwissen – Technische Mechanik. Springer, 2014.
- Gross, Hauger, Schröder, Wall: Technische Mechanik 1 – Statik. Springer, 11. Auflage, 2011.
- Sayir, Dual, Kaufmann, Mazza: Ingenieurmechanik 1 – Grundlagen und Statik. Springer, 3. Auflage, 2015.
- Spura: Technische Mechanik 1 – Stereostatik. Springer, 2016.
- Richard, Sander: Technische Mechanik – Statik. Springer, 5. Auflage, 2016.
- Dreyer: Technische Mechanik – Kinetik, Kinematik. Springer, 11. Auflage, 2012.
- ↑ Böge, Böge: Technische Mechanik. Springer, 31. Auflage, 2015, S. 4.
Dankert, Dankert: Technische Mechanik. Springer, 7. Auflage, 2013, S. 20, 23. - ↑ Gross, Hauger, Schröder, Wall: Technische Mechanik 1 – Statik. Springer, 11. Auflage, 2011, S. 51, 54.
Mahnken: Lehrbuch der Technischen Mechanik – Statik. Springer, 2012, S. 98, 103.
Spura: Technische Mechanik 1 – Stereostatik. Springer, 2016, S. 43, 46. - ↑ Dieter Meschede (Hrsg.): Gerthsen Physik. Springer, 25. Auflage, 2015, S. 72.
Bartelmann, Feuerbacher, Krüger, Lüst, Rebhan, Wipf (Hrsg.): Theoretische Physik. Springer, 2015, S. 28.
Achim Feldmeier: Theoretische Mechanik – Analysis der Bewegung. 2013, S. 83.
Torsten Fließbach: Mechanik – Lehrbuch zur Theoretischen Physik I. Springer, 7. Auflage, 2015, S. 18. - ↑ Wittenburg u. a. (Hrsg.): Das Ingenieurwissen – Technische Mechanik. Springer, 2014, S. 13.
- ↑ Mahnken: Lehrbuch der Technischen Mechanik – Statik. Springer, 2012, S. 145.
- ↑ Sayir, Dual, Kaufmann, Mazza: Ingenieurmechanik 1 – Grundlagen und Statik. Springer, 3. Auflage, 2015.
- ↑ Böge (Hrsg.): Handbuch Maschinenbau. Springer, 21. Auflage, 2013, S. C2.
- ↑ Dieter Meschede (Hrsg.): Gerthsen Physik. Springer, 25. Auflage, 2015, S. 73 f.
- ↑ Achim Feldmeier: Theoretische Mechanik – Analysis der Bewegung. 2013, S. 238–240.
- ↑ Gross, Hauger, Schröder, Wall: Technische Mechanik 1 – Statik. Springer, 11. Auflage, 2011, S. 73.
- ↑ Drehmoment. In: Lexikon der Physik. Abgerufen am 28. Oktober 2016.
- ↑ Böge: Technische Mechanik. Springer, 31. Auflage, S. 46.
- ↑ Dankert, Dankert: Technische Mechanik. Springer, 7. Auflage, 2013, S. 24.
- ↑ Mahnken, S. 24.
- ↑ Böge (Hrsg.): Handbuch Maschinenbau. Springer, 21. Auflage, 2013, S. C3.
- ↑ Dankert, Dankert: Technische Mechanik. Springer, 7. Auflage, 2013, S. 571.
- ↑ a b Gross u. a.: Technische Mechanik 3. Kinetik. Springer, 13. Auflage, 2014, S. 61.
- ↑ Conrad Eller: Holzmann/Meyer/Schumpich. Technische Mechanik. Kinematik und Kinetik. Springer, 12. Auflage, 2016, S. 127.
- ↑ Die Messwerte sind zeitliche Mittelwerte über einen vollen Arbeitszyklus, also über eine Umdrehung der Kurbelwelle beim Zweitaktmotor, über zwei Umdrehungen beim Viertaktmotor.


































































































