Hessscher Wärmesatz
Der Hess’sche Wärmesatz (auch Satz von Hess) dient der Berechnung von Enthalpieänderungen bei chemischen Reaktionen. Er wurde 1840 von Germain Henri Hess aufgestellt.
In vielen Fällen können Produkte einer chemischen Reaktion auf verschiedenen Wegen entstehen. Der Reaktionsweg hat dabei nach dem Energieerhaltungssatz keinen Einfluss auf die Energie, die bei einer Reaktion aufgenommen oder abgegeben wird. Nach dem Hess’schen Wärmesatz gilt dasselbe für die Enthalpie einer chemischen Reaktion.
Aussage
[Bearbeiten | Quelltext bearbeiten]Die Enthalpieänderung eines Gesamtprozesses ist die Summe der Enthalpieänderungen der einzelnen Prozessschritte.
Daraus folgt, dass die Reaktionsenthalpie nicht vom Reaktionsweg, sondern nur vom Anfangs- und vom Endzustand des Systems abhängt. Die Reaktionsenthalpie ist die Differenz aus der Bildungsenthalpie der Produkte minus der Bildungsenthalpie der Edukte. Meist wird der Satz unter der Annahme von Standardbedingungen ausgedrückt, gekennzeichnet durch eine hochgestellte Null ().
Erweiterungen
[Bearbeiten | Quelltext bearbeiten]Man kann den Hess’schen Satz auf die Gibbs-Energie erweitern:
Des Weiteren ist auch die Entropieänderung mit dem Hess’schen Satz berechenbar. Man beachte, dass Entropie die Einheit Joule pro Kelvin besitzt und eine absolute Größe ist (kein Delta in der Summe!):
Beispiel
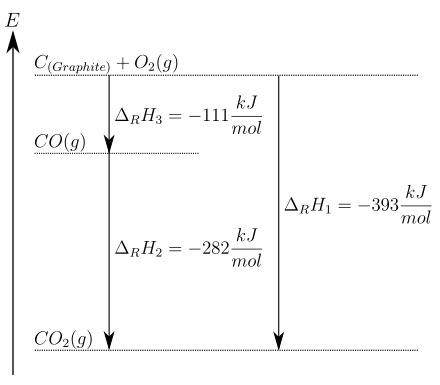
[Bearbeiten | Quelltext bearbeiten]Graphit kann direkt zu Kohlenstoffdioxid verbrannt werden (1) oder indirekt über die Zwischenstufe Kohlenstoffmonoxid (2), (3):
Die Gesamtreaktionsenthalpie ist in beiden Fällen gleich:
Literatur
[Bearbeiten | Quelltext bearbeiten]- Chemie heute Sekundarbereich II, Schroedel Verlag, 1998, ISBN 3-507-10630-2.
- Silberberg: Chemistry, The Molecular Nature of Matter and Change. Fourth Edition. Mc Graw Hill, 2006, ISBN 0-07-111658-3.
- Fokus Chemie, Sekundarstufe II. Cornelsen Verlag, 2018, ISBN 978-3-06-015656-6.
Weblinks
[Bearbeiten | Quelltext bearbeiten]Video: Satz von HESS und Thermochemie – Wie viel Wärme wird bei chemischen Reaktionen frei?. Jakob Günter Lauth (SciFox) 2013, zur Verfügung gestellt von der Technischen Informationsbibliothek (TIB), doi:10.5446/15661.







