Isoparametrische Elemente
Isoparametrische Elemente sind in der Finite-Elemente-Methode (FEM) benutzte Formulierungen für Finite-Elemente, die in der Analyse von Festkörpern weit verbreitet sind. Die FEM ist ein numerisches Verfahren zur Lösung von Differentialgleichungen, deren eindeutige Lösung gewisser Zusatzbedingungen, sogenannter Anfangs- und Randbedingungen, bedarf. Die Lösung des Anfangsrandwertproblems wird in der FEM in Ansatzfunktionen entwickelt, die potenziell jede zum Vergleich zugelassene Lösungsfunktion zu approximieren vermögen. Durch Einschränkung der Ansatzfunktionen auf eine endliche Anzahl stellt sich ein Diskretisierungsfehler ein. Nun wird die Lösung additiv in zwei Anteile aufgespalten: den einen, der die Anfangsbedingung wiedergibt, und den anderen, der an die Randbedingungen anzupassen ist. Nun könnte man diese beiden Anteile mit verschiedenen Ansatzfunktionen approximieren. Das Besondere an den isoparametrischen Elementen ist, dass sie für beide Lösungsanteile dieselben Ansatzfunktionen benutzen. Die Standardformulierung der FEM ist die Verschiebungsmethode. Damit dort ein ortsunabhängiges Verschiebungsfeld dargestellt werden kann, müssen die Ansatzfunktionen gewissen Anforderungen genügen, die in isoparametrischen Elementen besonders leicht zu erfüllen sind. Isoparametrische Elemente haben die Vorteile, dass
- sie in den meisten Problemstellungen einsetzbar sind,
- in ihnen ein konstantes Verschiebungsfeld einfach darzustellen ist,
- sich der Diskretisierungsfehler leicht, im Präprozessor visuell, einschätzen lässt und
- nur ein Satz Ansatzfunktionen zu definieren und zu programmieren ist.
Lösung von Differentialgleichungen
[Bearbeiten | Quelltext bearbeiten]Die FEM ist eine Methode zur Lösung von Differentialgleichungen (Dgl) und deshalb soll die Lösung solcher Gleichungen hier eingangs an einem kleinen Beispiel skizziert werden. Die Bewegungsgleichung eines Massepunktes mit Masse m, an dem eine Kraft F angreift, lautet nach dem zweiten Newton’schen Gesetz
Der Ort des Massepunktes wird von der Bewegungsfunktion χ(t) als Funktion von der Zeit t angegeben und die zwei aufgesetzten Punkte symbolisieren die zweite Zeitableitung (Beschleunigung). Gesucht sei eine Lösung im Zeitintervall [0,1]. Bei konstanter Kraft kann diese Dgl geschlossen integriert werden:
Diese Lösung enthält neben der gesuchten Funktion χ(t), der Masse m und der Zeit t drei Variablen: X, v0 und F, die in einem konkreten Berechnungsfall zu spezifizieren sind. Die zum Bewegungsbeginn vorherrschenden Bedingungen sind die Anfangsbedingungen, die hier durch die Position X und Geschwindigkeit v0 zur Zeit t=0 bestimmt sind. Die Kraft F gehört zu den, im Allgemeinen von der Zeit und vom Ort abhängigen Randbedingungen.
Die Funktionen χh(t), die zur Zeit t=0 den homogenen Anfangs- und Randbedingungen
genügen, können in beliebiger Weise zu einer gegebenen Lösung der Dgl addiert werden, ohne dass diese Anfangs- und Randbedingungen verletzt würden. In diesem Beispiel wäre bei konstanter Kraft
Die partikuläre Lösung χp(t) genügt hingegen den inhomogenen Anfangs- und Randbedingungen[1]
Die vollständige Lösung der Dgl ist die Summe aus der partikulären Lösung und den homogenen Lösungsanteilen:
Die Verschiebung des Körpers ist die Differenz zwischen seiner aktuellen Position χ(t) und seiner Ausgangsposition X und ist mithin der zeitabhängige Teil der Lösungsfunktion
wohingegen die Ausgangsposition X=χ(t)-u(t) der zeitunabhängige Teil der Lösungsfunktion ist. Bei der näherungsweisen Lösung einer Dgl mit der Methode der gewichteten Residuen (Ritzsches Variationsverfahren) wird für die gesuchte Lösung ein funktionaler Ansatz gemacht, mit der die exakte Lösung approximiert werden kann, z. B.:
Dieser Ansatz wird in die Dgl eingesetzt, die so in aller Regel nicht exakt erfüllt wird. Der Rest ist das Residuum
Der Faktor A wird gemäß dem Galerkin-Ansatz berechnet, indem das Residuum mit der Ansatzfunktion multipliziert, über das interessierende Intervall, hier [0,1], integriert wird und dieser gewichtete Rest zum Verschwinden gebracht wird:
So entsteht die homogene Näherungslösung
Diese ist noch durch die partikulären Anteile zu ergänzen, um die Anfangs- und Randbedingungen zu berücksichtigen:
Die Finite-Elemente-Methode
[Bearbeiten | Quelltext bearbeiten]Beim klassischen Ritz-Ansatz wird die Lösungsfunktion durch eine Summe von Funktionen ersetzt, die von einem Parametervektor abhängt und jede zum Vergleich zugelassene Funktion approximieren kann[1]. Die Lösung der Dgl wird somit von der Suche nach einer Funktion auf die Suche nach einem Parametervektor reduziert.
Die Anfangspositionen der Partikel – die Geometrie des Körpers – ist wie dargelegt ein partikulärer Lösungsanteil der Dgl, der den Anfangsbedingungen gehorcht. Vereinfachungen ergeben sich durch folgende, über das Ritz’sche Verfahren und den Galerkin-Ansatz hinausgehenden Annahmen der FEM:
- Da das Auffinden der partikulären Lösung in den meisten Fällen schwierig ist, wird auch diese wie die Lösungsfunktion in Summen von Funktionen entwickelt. Die Parameter der Ansatzfunktionen sind so zu wählen, dass die Anfangs- und Randbedingungen (Körpergeometrie, Anfangsgeschwindigkeit) befriedigt sind.
- Die Zeit- und Ortsabhängigkeit der Ansatzfunktionen wird in rein ortsabhängige Funktionen und nur zeitabhängige Parameter aufgeteilt.
In der ingenieursgemäßen Vorgehensweise werden physikalisch bedeutsame Größen, wie die Koordinaten oder Verschiebungen bestimmter Punkte als Parameter gewählt. So sind die Parameter leicht zu ermitteln und ihre Plausibilität einfach zu überprüfen.
Standardformulierung
[Bearbeiten | Quelltext bearbeiten]Die erste Anwendung der FEM war die lineare Behandlung von Festkörpern und Strukturen und davon ausgehend hat die FEM ihre Anstöße erhalten. Bei der Berechnung von Problemen der Festkörpermechanik werden Verschiebungen gesucht, welche die Translation, Rotation und Verformung eines Körpers wiedergeben. Während der Entwicklung der FEM wurde eine Vielzahl von Möglichkeiten zur Beschreibung der Geometrie und der Verschiebungen aufgezeigt. Die Standardformulierung ist die Verschiebungsmethode, bei der die Verschiebungen an ausgesuchten Punkten, den Knoten, als Parameter gewählt und die Verschiebungen zwischen den Knoten mit Formfunktionen interpoliert werden.
Die sogenannten gemischten Methoden benutzen neben den Knotenverschiebungen noch weitere Unbekannte, die physikalisch einem Druck, einer Spannung oder Dehnung entsprechen. Die Elementverschiebungen ergeben sich dann aus einem Zusammenspiel all dieser Variablen. Die isoparametrischen Elemente stellen den Zusammenhang zwischen den Elementverschiebungen und den Knotenverschiebungen direkt her[2]. Hier haben die isoparametrischen Elemente neben den oben genannten Vorteilen den weiteren, dass sich das Verschiebungsfeld leicht visualisieren lässt.
Verschiebungsmethode
[Bearbeiten | Quelltext bearbeiten]In der wichtigen und anschaulichen Anwendung der Verschiebungsmethode in der Festkörpermechanik wird für einen Körper die Bewegungsfunktion für alle seine Partikel in Abhängigkeit von der Zeit gesucht. Statt des gesamten Körpers kann an dieser Stelle auch jeder beliebige Teilkörper betrachtet werden und so kann auch jedes Finite-Element, das einen Teilkörper modelliert, als Körper angenommen werden. Das soll im Folgenden auch geschehen. Auf den Zusammenbau des Körpers aus Finiten-Elementen wird am Schluss kurz eingegangen.
Lokale Elementkoordinaten
[Bearbeiten | Quelltext bearbeiten]Für die mathematische Beschreibung wird jedem Partikel P eineindeutig durch eine Referenzkonfiguration ein Koordinatenvektor zugewiesen, was gestattet jedes Partikel mit seinem Koordinatenvektor zu identifizieren: . Der Einfachheit halber definiert jedes Element seine eigene Referenzkonfiguration, weshalb dort lokale Koordinaten genannt werden, denn sie gelten nur im betrachteten Finiten-Element. Üblicherweise ist je nach Dimension d des Elementes. Die Koordinaten sind weitgehend beliebig und unterscheiden sich im Allgemeinen von den räumlichen Koordinaten des Partikels.
Bewegungsfunktion
[Bearbeiten | Quelltext bearbeiten]Für alle Partikel im Element wird jetzt die Bewegungsfunktion gesucht, die die Dgl und die Anfangs- und Randbedingungen erfüllt. Der Ortsvektor entspricht der räumlichen Position des Partikels zur Zeit t, so dass die Bewegungsfunktion bei festgehaltenem Partikel die Bahnlinie des Partikels beschreibt.
Für die Anwendung der FEM wird eine endliche Menge von Partikeln
ausgewählt, deren Elemente Knoten genannt werden und die das Element aufspannen. Die Knoten, die der Beschreibung der Geometrie dienen, seien Elemente der Menge und besitzen Nummern aus der Indexmenge und diejenigen Knoten, die für die Beschreibung der Verschiebungen benutzt werden seien Elemente der Menge mit Nummern aus der Indexmenge .
Geometrische Beschreibung des Körpers
[Bearbeiten | Quelltext bearbeiten]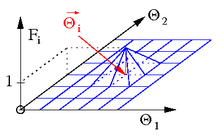

Die Form des Elementes in der zeitunabhängigen Ausgangskonfiguration zu Beginn der Bewegung zur Zeit stellt – wie oben dargelegt – eine Anfangsbedingung dar. Der geometrische Ortsvektor gibt die räumliche Position des Partikels zur Zeit an und ist somit ein Objekt unserer Anschauung. Der Ortsvektor eines jeden Partikels wird in eine Summe von stetigen Formfunktionen
entwickelt, worin Fi die Formfunktion und der Koordinatenvektor des i-ten Knotens ist. Die Funktionen liefern für genau einen Knoten den Wert eins und für alle anderen Knoten den Wert null
siehe Abb. 1. Die Positionen der Knoten in werden so mit den Formfunktionen exakt wiedergegeben
und die Positionen der zwischen den Knoten liegenden Partikel werden mit den Formfunktionen interpoliert, was namensgebend für diese Funktionen ist. Wenn der Verlauf der Formfunktionen zwischen den Knoten nicht der Form des Körpers entspricht, dann entsteht der (in Abwesenheit einer analytischen Lösung unvermeidliche) Diskretisierungsfehler, siehe Abb. 2.
Verschiebungsfeld
[Bearbeiten | Quelltext bearbeiten]
Der Differenzvektor
zwischen der momentanen Lage eines Partikels und seiner Ausgangslage ist der Verschiebungsvektor, der der zeitabhängige Teil der Bewegungsfunktion ist und der in eine Summe von Produkten von stetigen, rein ortsabhängigen Ansatzfunktionen und rein zeitabhängigen Knotenvariablen entwickelt wird:
Die Ansatzfunktionen Hi liefern für genau einen Knoten den Wert eins und für alle anderen Knoten den Wert null:
Der Parametervektor enthält die im Allgemeinen zeitabhängigen Verschiebungen des Knotens i. Es können mehr () oder weniger () Knoten benutzt werden als für die Beschreibung der Ausgangsposition herangezogen werden, was die sub- bzw. superparametrischen Elemente auch tun, siehe Abb. 3.
Konstantes Verschiebungsfeld
[Bearbeiten | Quelltext bearbeiten]Die Bewegungsfunktion lautet mit diesen beiden Ansätzen:
Um physikalisch Sinn zu machen, müssen die Ansatzfunktionen in der Lage sein, eine Parallelverschiebung des Körpers darzustellen. Bei einer Parallelverschiebung werden alle Partikel und damit auch alle Knoten des Modells ortsunabhängig mit dem Vektor verschoben. Dann lautet das Verschiebungsfeld
weshalb
(I)
| ||
zu fordern ist. Ebenso ist zu fordern, dass der verschobene Körper auch mit einer verschobenen Anfangsposition dargestellt werden kann:
Wegen Bedingung (I) folgt daraus:
(II)
| ||
Isoparametrische Elemente
[Bearbeiten | Quelltext bearbeiten]Die erste zu bemerkende Eigenschaft isoparametrischer Elemente ist, dass für die Wiedergabe der Verschiebung dieselben Knoten wie für die Geometrie benutzt werden:
Die zweite Eigenschaft isoparametrischer Elemente ist, dass für die Darstellung der Verschiebung dieselben, stetigen, Formfunktionen wie für die Ausgangsposition benutzt werden
Dem Galerkin-Ansatz folgend, werden für die Wichtungsfunktionen dieselben Funktionen genommen wie für die Geometrie und Verschiebung. Diese Eigenschaften bewirken, dass
- die Formfunktionen nur die Forderung (I) erfüllen brauchen, da dann (II) automatisch erfüllt ist,
- sich der Diskretisierungsfehler leicht, im Präprozessor visuell, einschätzen lässt und
- nur ein Satz Formfunktionen für die Geometrie, die Verschiebungen und die Wichtungsfunktionen zu definieren und zu programmieren ist.
Modellierung des ganzen Körpers
[Bearbeiten | Quelltext bearbeiten]Die Bewegungsfunktion muss im Element stetig sein und das ist auch für die globale Bewegungsfunktion des gesamten Festkörpers zu fordern. Üblicherweise wird festgelegt, dass die lokale, im Element definierte Bewegungsfunktion außerhalb des Elementes verschwindet und die globale Bewegungsfunktion die Summe aller lokalen Element-Bewegungsfunktionen ist. Damit die globale Bewegungsfunktion stetig ist, müssen benachbarte Elemente kompatibel sein, so dass sie den Körper überschneidungsfrei und lückenlos aufbauen. Das bedeutet, dass benachbarte Elemente an ihrer gemeinsamen Berandungsfläche dieselben Knoten und denselben Verlauf der Formfunktionen besitzen, siehe Abb. 2 und 3.
Beispiel
[Bearbeiten | Quelltext bearbeiten]
Ein ein-dimensionales isoparametrisches Stab-Element besitze die lokale Koordinate
entlang seiner Achse, s. Bild. Mit den Formfunktionen
kann jeder Punkt auf seiner Achse dargestellt werden:
Die Anforderung (I) an die Formfunktionen wird in diesem Element erfüllt:
Somit kann das Element eine Translation im Raum beschreiben.
Fußnoten
[Bearbeiten | Quelltext bearbeiten]Literatur
[Bearbeiten | Quelltext bearbeiten]- Klaus-Jürgen Bathe: Finite-Elemente-Methoden: Matrizen und lineare Algebra, die Methode der finiten Elemente, Lösung von Gleichgewichtsbedingungen und Bewegungsgleichungen. Springer 1986, ISBN 3-540-15602-X.
- Klaus Knothe, Heribert Wessels: Finite Elemente: eine Einführung für Ingenieure. Springer, 2008. ISBN 3-540-72188-6.
- H.R. Schwarz: Methode der finiten Elemente. Teubner, Stuttgart 1980.
- Peter Wriggers: Nichtlineare Finite-Element-Methoden. Springer, 2001. ISBN 3-540-67747-X.









![{\displaystyle \int _{0}^{1}t^{2}(2mA-F)\,\mathrm {d} t=(2mA-F)\left[{\frac {t^{3}}{3}}\right]_{0}^{1}={\frac {1}{3}}(2mA-F){\stackrel {\displaystyle !}{=}}0\quad \rightarrow \quad A={\frac {F}{2m}}\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4185ff5c6c30c80174e9dbfa9005869247270621)





![{\displaystyle V_{R}=[-1,1]^{d}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08a89ed762c5a987a405f6def34ac7d5271bd052)














![{\displaystyle F_{i}({\vec {\Theta }}_{j})=\left\{{\begin{array}{ll}1&\mathrm {falls} \;i,j\in I_{x}\;\mathrm {und} \;i=j\\[1ex]0&\mathrm {falls} \;i,j\in I_{x}\;\mathrm {und} \;i\neq j\end{array}}\right.\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c7365b51c17feea9c0d0a0379bbd729d1eb8e1d)





![{\displaystyle H_{i}({\vec {\Theta }}_{j})=\left\{{\begin{array}{ll}1&\mathrm {falls} \;i,j\in I_{u}\;\mathrm {und} \;i=j\\[1ex]0&\mathrm {falls} \;i,j\in I_{u}\;\mathrm {und} \;i\neq j\end{array}}\right.\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c00254ec9a761a5233ffc6eea96f278ce2486ba)











![{\displaystyle \Theta \in [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2316bc975b1e96f2762b3d1ceaf7b658b94ed355)



