Logistische Gleichung
Die logistische Gleichung wurde ursprünglich 1837 von Pierre François Verhulst[1] als demographisches mathematisches Modell eingeführt. Die Gleichung ist ein Beispiel dafür, wie komplexes, chaotisches Verhalten aus einfachen nichtlinearen Gleichungen entstehen kann. Infolge einer richtungsweisenden Arbeit des theoretischen Biologen Robert May aus dem Jahr 1976[2] fand sie weite Verbreitung. Bereits 1825 stellte Benjamin Gompertz in einem verwandten Zusammenhang eine ähnliche Gleichung vor.[3]
Die zugehörige Dynamik kann anhand eines sogenannten Feigenbaumdiagramms (siehe unten) veranschaulicht werden. Eine wichtige Rolle spielt dabei die schon 1975 von Mitchell Feigenbaum gefundene Feigenbaum-Konstante.
Das demographische Modell[Bearbeiten | Quelltext bearbeiten]
Für den stetigen Fall siehe logistische Funktion.
Es werden mathematische Gesetzmäßigkeiten gesucht, die die Entwicklung einer Population modellhaft darstellen. Aus der Größe der Population zu einem gewissen Zeitpunkt soll auf die Größe nach einer Fortpflanzungsperiode (z. B. nach einem Jahr) geschlossen werden.
Das logistische Modell berücksichtigt zwei Einflüsse:
- Durch Fortpflanzung vermehrt sich die Population geometrisch. Die Individuenzahl ist im Folgejahr um einen Wachstumsfaktor größer als die aktuelle Population.
- Durch Verhungern verringert sich die Population. Die Individuenzahl vermindert sich in Abhängigkeit von der Differenz zwischen ihrer aktuellen Größe und einer theoretischen Maximalgröße mit der Proportionalitätskonstante . Der Faktor, um den sich die Population vermindert, hat also die Gestalt .
Um bei der Berechnung der Population im Folgejahr beide Prozesse zu berücksichtigen, multipliziert man die aktuelle Population sowohl mit dem Vermehrungsfaktor als auch mit dem Hungerfaktor . Man erhält damit die logistische Gleichung
- .
Um die folgenden mathematischen Untersuchungen zu vereinfachen, wird die Populationsgröße oft als Bruchteil der Maximalgröße angegeben:
- .
Außerdem werden , und zusammengefasst zum Parameter :
- .
Damit ergibt sich die folgende Schreibweise für die logistische Gleichung:
- .
Hierbei ist die Kapazität des Biotops. Das heißt, es ist die Population, die bei geeigneter Wahl von dem Fixpunkt der Dynamik entspricht.
Das mathematische Modell[Bearbeiten | Quelltext bearbeiten]
Man kann ohne Beschränkung der Allgemeinheit setzen. Dann ergibt sich
- .
ist dabei eine Zahl zwischen und . Sie repräsentiert die relative Größe der Population im Jahr . Die Zahl steht also für die Startpopulation (im Jahr 0). Der Parameter ist immer positiv, er gibt die kombinierte Auswirkung von Vermehrung und Verhungern wieder.
Verhalten in Abhängigkeit von r[Bearbeiten | Quelltext bearbeiten]
Die Animation unten zeigt Zeitreihenentwicklungen der Logistischen Gleichung im Zeit- und Frequenzbereich (Fourier-Analysis), die sich für wachsende Parameter ergeben. Startwert ist jedes Mal .
Gut sichtbar sind die Zonen der Intermittenz innerhalb des deterministischen Chaos.
Bei verschiedenen können die folgenden Verhaltensweisen für große beobachtet werden. Dabei hängt dieses Verhalten nicht vom Anfangswert ab, sondern nur von :
- Mit von 0 bis 1 stirbt die Population in jedem Fall aus.
- Mit zwischen 1 und 2 nähert sich die Population monoton dem Grenzwert an.
- Mit zwischen 2 und 3 nähert sich die Population dem Grenzwert alternierend, d. h. die Werte liegen ab einem bestimmten abwechselnd über und unter dem Grenzwert.
- Mit zwischen 3 und (etwa 3,45) wechselt die Folge bei fast allen Startwerten (ausgenommen 0, 1 und ) zwischen den beiden Umgebungen zweier Häufungspunkte.
- Mit zwischen und ungefähr 3,54 wechselt die Folge bei fast allen Startwerten zwischen den Umgebungen von vier Häufungspunkten.
- Wird größer als 3,54, stellen sich erst 8, dann 16, 32 usw. Häufungspunkte ein. Die Intervalle mit gleicher Anzahl von Häufungspunkten (Bifurkationsintervalle) werden immer kleiner; das Längenverhältnis zweier aufeinanderfolgender Bifurkationsintervalle nähert sich der Feigenbaumkonstanten. Diese Konstante ist auch in anderen mathematischen Zusammenhängen von Bedeutung. (Zahlenwert: δ ≈ 4,6692016091029906718532038204662016172581…).
- Bei annähernd 3,57 beginnt das Chaos: Die Folge springt zunächst periodisch zwischen den Umgebungen der nun instabilen Häufungspunkte umher. Mit weiter wachsendem verschmelzen diese Intervalle so, dass sich deren Anzahl im Rhythmus der Feigenbaumkonstante halbiert, bis es nur noch ein Intervall gibt, in dem die Folge chaotisch ist. Perioden sind dann nicht mehr erkennbar. Winzige Änderungen des Anfangswertes resultieren in unterschiedlichsten Folgewerten – eine Eigenschaft des Chaos.
- Bei vielen Koeffizienten zwischen 3,57 und 4 kommt es zu chaotischem Verhalten, obwohl für bestimmte wieder Häufungspunkte (d. h. stabile periodische Orbits, gegen die fast jeder Anfangswert konvergiert) vorhanden sind. Beispielsweise existieren in der Nähe von bei steigendem erst 3, dann 6, 12 usw. Häufungspunkte. Ebenso gibt es r-Werte mit 5 oder mehr Häufungspunkten – alle Periodendauern tauchen auf.
- Drei tiefliegende mathematische Sätze besagen folgendes: (1) jedes noch so kleine Intervall von Koeffizienten enthält Parameter, für die es stabile periodische Orbits gibt (so dass die Dynamik eben nicht chaotisch ist): also nicht-chaotische Parameter sind "dicht" im Intervall der Koeffizienten. Chaotische Parameter enthalten also keine Intervalle. Aber (2) die chaotischen Parameter haben positives Maß: also mit echt positiver Wahrscheinlichkeit liefert ein zufälliger Parameter chaotische Dynamik. Schließlich (3) hat fast jeder reelle Koeffizient (im Sinne voller Wahrscheinlichkeit) entweder einen stabilen periodischen Orbit (gegen den fast jeder Anfangswert konvergiert) oder ist in strengem Sinne "chaotisch". (Weitere dynamische Möglichkeiten gibt es, haben aber Wahrscheinlichkeit null.)
- Für größer 4 divergiert die Folge für fast alle Anfangswerte und verlässt das Intervall .
Dieser Übergang von konvergentem Verhalten über Periodenverdopplungen zu chaotischem Verhalten ist generell für nichtlineare Systeme typisch, die in Abhängigkeit von einem Parameter chaotisches oder nicht-chaotisches Verhalten zeigen.
Eine Erweiterung des Wertebereiches auf die komplexen Zahlen führt nach einer Koordinatentransformation zur Mandelbrotmenge.
Beispiel[Bearbeiten | Quelltext bearbeiten]
Die „logistische Kurve“ mit einer Wachstumsrate verläuft S-förmig. Ab einem Wert um 3,6 bricht Chaos aus, wie die Abbildung mit illustriert.[4]


Graphische Darstellung[Bearbeiten | Quelltext bearbeiten]
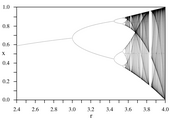
Das folgende Bifurkationsdiagramm, bekannt als Feigenbaum-Diagramm, fasst diese Beobachtungen zusammen. Die horizontale Achse gibt den Wert des Parameters an und die vertikale Achse die Häufungspunkte für die Folge .
-
Bifurkationsdiagramm der logistischen Gleichung
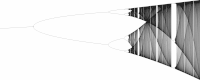
-
Hochauflösende Version ohne Skala
-
Hochauflösender Ausschnitt des Bifurkationsdiagramms der logistischen Gleichung
-
Zusammenhang mit der Mandelbrotmenge (nach Koordinatentransformation)
Analytische Lösung[Bearbeiten | Quelltext bearbeiten]
Für den Parameter existiert eine analytische Lösung:
- .
Für die Parameter und können ebenfalls analytische Lösungen angegeben werden.
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Pierre-François Verhulst: Notice sur la loi que la population suit dans son accroissement. In: Correspondance Mathématique et Physique. Band 10, 1838, ZDB-ID 428605-4, S. 113–121.
- ↑ Robert May: Simple mathematical models with very complicated dynamics Nature V. 261, S. 459–467 (10 Juni 1976)
- ↑ Benjamin Gompertz: On the Nature of the Function Expressive of the Law of Human Mortality, and on a New Mode of Determining the Value of Life Contingencies. In: Philosophical Transactions of the Royal Society of London. Vol. 115, 1825, ISSN 0260-7085, S. 513–585.
- ↑ Jürgen Beetz: 1 + 1 = 10. Mathematik für Höhlenmenschen. Springer, Heidelberg 2012, ISBN 978-3-8274-2927-8, S. 313 f.



























![{\displaystyle [0;1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc3bf59a5da5d8181083b228c8933efbda133483)