Subdifferential

Das Subdifferential ist eine Verallgemeinerung des Gradienten auf nicht differenzierbare konvexe Funktionen. Das Subdifferential spielt eine wichtige Rolle in der konvexen Analysis sowie der konvexen Optimierung.

Definition

Sei $f\colon \mathbb {R} ^{n}\to \mathbb {R}$ eine konvexe Funktion. Ein Vektor $g\in \mathbb {R} ^{n}$ heißt Subgradient von $f$ an der Stelle $x_{0}$, wenn für alle $x\in \mathbb {R} ^{n}$ gilt

$f(x)\geq f(x_{0})+\langle g,x-x_{0}\rangle$,

wobei $\langle \cdot ,\cdot \rangle$ das Standardskalarprodukt bezeichnet.

Das Subdifferential $\partial f(x_{0})$ ist die Menge aller Subgradienten von $f$ im Punkt $x_{0}$.

Existieren die folgenden Grenzwerte

$$a=\lim _{x\to x_{0}^{-}}{\frac {f(x)-f(x_{0})}{x-x_{0}}},$$

$$b=\lim _{x\to x_{0}^{+}}{\frac {f(x)-f(x_{0})}{x-x_{0}}},$$

so wird das Intervall $[a,b]$ aller Subgradienten "das Subdifferential der Funktion $f$ bei $x_{0}$" genannt und wird als $\partial f(x_{0}):=[a,b]$ geschrieben.

Für eine konvexe Funktion gilt $a\leq b$, für eine nicht konvexe Funktion gilt dies nicht und daher ist $\partial f(x_{0})=\emptyset$.

Anschauung

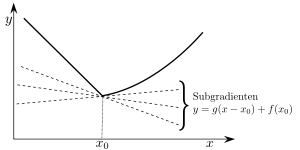
Subgradienten einer konvexen Funktion

Intuitiv bedeutet diese Definition für $n=1$, dass der Graph der Funktion $f$ überall über der Geraden $G$ liegt, die durch den Punkt $(x_{0},f(x_{0}))$ geht und die Steigung $g$ besitzt:

$G=\{(x,y)\in \mathbb {R} ^{2}\mid y=g\cdot (x-x_{0})+f(x_{0})\}$

Da die Normalengleichung von $G$ gerade

$-g\cdot (x-x_{0})+1\cdot (y-f(x_{0}))=0$

ist, ist die Normale an $G$ also $(-g,1)\in \mathbb {R} ^{2}$.

Im allgemeinen Fall $n\geq 1$ liegt $f$ über der Hyperebenen, die durch den Fußpunkt $(x_{0},f(x_{0}))$ und die Normale $(-g,1)\in \mathbb {R} ^{n+1}$ gegeben ist.

Wegen des Trennungssatzes ist das Subdifferential einer stetigen konvexen Funktion überall nicht leer.

Beispiel

Das Subdifferential der Funktion $f\colon \mathbb {R} \rightarrow \mathbb {R}$, $x\mapsto |x|$ ist gegeben durch:

$\partial f(x_{0})={\begin{cases}\{-1\}&x_{0}<0\\\left[-1,1\right]&x_{0}=0\\\{1\}&x_{0}>0\end{cases}}$

Eine ähnliche Eigenschaft ist bei der Lasso-Regression für die Herleitung der Soft-Threshold-Funktion wichtig.

Beschränktheit

Sei $f\colon \mathbb {R} ^{n}\rightarrow \mathbb {R}$ stetig und sei $X\subset \mathbb {R} ^{n}$ beschränkt. Dann ist die Menge $\bigcup _{x_{0}\in X}\partial f(x_{0})$ beschränkt.

Beweis

Sei $f\colon \mathbb {R} ^{n}\rightarrow \mathbb {R}$ stetig und sei $X\subset \mathbb {R} ^{n}$ beschränkt. Setze $\varepsilon :=\sup |f({\overline {U_{1}(X)}})|$ wobei ${\overline {U_{1}(X)}}=\{x\in \mathbb {R} ^{n}\mid {\rm {dist}}(x,X)\leq 1\}$. Angenommen $\bigcup _{x_{0}\in X}\partial f(x_{0})$ ist nicht beschränkt, dann gibt es für $R:=2\varepsilon$ ein $x_{0}\in X$ und ein $g\in \partial f(x_{0})$ mit $\|g\|_{2}>R=2\varepsilon$. Sei $x:={\frac {1}{\|g\|_{2}}}g+x_{0}$. Somit sind $x_{0},x\in {\overline {U_{1}(X)}}$. Wir erhalten die Abschätzung

$g^{T}(x-x_{0})={\frac {1}{\|g\|_{2}}}g^{T}g=\|g\|_{2}>2\varepsilon \geq \left|f(x)-f(x_{0})\right|\geq f(x)-f(x_{0})$.

$g$ ist also kein Subgradient. Das ist ein Widerspruch.

Differenzierbarkeit

Ist die Funktion differenzierbar in $x_{0}\in \mathrm {int} \,\mathrm {dom} \,f$, so gilt:

$\partial f(x_{0})=\left\{\nabla f(x_{0})\right\}$

Siehe für einen Beweis.

Zudem gilt: Ist das Subdifferential $\partial f(x_{0})$ einelementig, so ist $f$ an der Stelle $x_{0}$ differenzierbar.