Konvexe und konkave Funktionen


In der Analysis heißt eine reellwertige Funktion konvex (lateinisch convexus ‚nach oben oder unten gewölbt‘), wenn ihr Graph unterhalb jeder Verbindungsstrecke zweier seiner Punkte liegt. Dies ist gleichbedeutend dazu, dass der Epigraph der Funktion, also die Menge der Punkte oberhalb des Graphen, eine konvexe Menge ist.
Eine reellwertige Funktion heißt konkav (lateinisch: concavus = gewölbt), wenn ihr Graph oberhalb jeder Verbindungsstrecke zweier seiner Punkte liegt. Dies ist gleichbedeutend dazu, dass der Hypograph der Funktion, also die Menge der Punkte unterhalb des Graphen, eine konvexe Menge ist.
Einer der ersten, der sich mit den Eigenschaften konvexer und konkaver Funktionen beschäftigte, war der dänische Mathematiker Johan Ludwig Jensen. Die nach ihm benannte Jensensche Ungleichung ist Grundlage wichtiger Resultate in der Wahrscheinlichkeitsrechnung, Maßtheorie und Analysis.
Die besondere Bedeutung konvexer bzw. konkaver Funktionen liegt darin, dass sie eine weitaus größere Gruppe als die linearen Funktionen bilden, aber ebenfalls viele einfach zu untersuchende Eigenschaften haben, welche Aussagen über nichtlineare Systeme ermöglichen. Da beispielsweise jedes lokale Minimum einer konvexen Funktionen auch ein globales Minimum ist, sind sie bei vielen Optimierungsproblemen von Bedeutung (siehe auch: Konvexe Optimierung). Selbst für konvexe Funktionale, die auf unendlichdimensionalen Räumen definiert sind, lassen sich unter bestimmten Voraussetzungen ähnliche Aussagen treffen. Daher spielt Konvexität auch eine wichtige Rolle in der Variationsrechnung.
Definition[Bearbeiten | Quelltext bearbeiten]

Es gibt zwei äquivalente Definitionen, einerseits kann man Konvexität anhand einer Ungleichung über die Funktionswerte definieren (analytische Definition), andererseits über die Konvexität von Mengen (geometrische Definition).
Analytische Definition[Bearbeiten | Quelltext bearbeiten]
Eine Funktion , wobei eine konvexe Teilmenge des ist, heißt konvex, wenn für alle aus und für alle gilt, dass
Hieraus lässt sich die Bedingung im Kopftext herleiten, dass der Graph der Funktion unterhalb der Verbindungsstrecke zweier seiner Punkte liegt.
| Rechnerische Veranschaulichung der Herleitung |
|
Die nachfolgend beschriebenen geometrischen Objekte bebildern die analytische Aussage und ermöglichen in den Fällen oder eine anschaulichen Vorstellung derselben.
Der Punkt sei die Koordinatendarstellung einer Abszisse . Dazu sei die Koordinatendarstellung eines Punktes des Graphen von mit Ordinate . lässt sich auch als ordinatenparallele Projektion von in den Abszissenraum auffassen. In der Schreibweise werden die Koordinaten der Abszisse durch den Punkt , den sie definieren, dargestellt.
Die Gerade durch die Punkte und des Graphen von hat eine Parameterform
hierbei ist der allgemeine Punkt und ein Richtungsvektor von . durchläuft für wachsende alle Punkte der Gerade von bis , wie die Betrachtung der -fachen von zeigt. Die ordinatenparallele Projektion des Punktes in den Abszissenraum ist ein nachfolgend als bezeichneter Punkt. hat die Ordinate .
hierbei ist der allgemeine Punkt und ein Richtungsvektor von . durchläuft für wachsende alle Punkte der Gerade von bis , wie die Betrachtung der -fachen von zeigt. Da der Definitionsbereich von als konvex vorausgesetzt ist, enthält er alle mit .
durchläuft für wachsende alle sich ordinatenparallel auf projizierenden Punkte des Graphen von von bis , wie die Betrachtung der -fachen von zeigt.
Die analytische Definition der Konvexität von : verlangt, dass für die betrachteten die Ordinate von höchstens so groß ist wie die Ordinate von . Insofern verläuft der Graph von unterhalb der Verbindungsstrecke . Dies war zu veranschaulichen. |
Geometrische Definition[Bearbeiten | Quelltext bearbeiten]
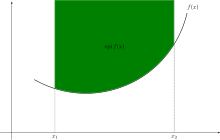
Eine Funktion () heißt konvex, wenn ihr Epigraph eine konvexe Menge ist. Diese Definition hat gewisse Vorteile für erweiterte reelle Funktionen, welche auch die Werte annehmen können und bei denen mit der analytischen Definition der undefinierte Term auftreten kann.[1] Aus der Konvexität des Epigraphen ergibt sich außerdem, dass die Definitionsmenge eine konvexe Menge ist. Eine konvexe Funktion hat also immer eine konvexe Definitionsmenge, umgekehrt ist eine Funktion nicht konvex, wenn ihre Definitionsmenge nicht konvex ist.
Konkave Funktionen[Bearbeiten | Quelltext bearbeiten]
Ist eine konvexe Funktion, so heißt konkav. Für konkave Funktionen drehen sich die Definitionen jeweils um, die analytische Definition einer konkaven Funktion lautet also
die geometrische Definition einer konkaven Funktion fordert, dass der Hypograph eine konvexe Menge ist.
Weitere Klassifizierungen[Bearbeiten | Quelltext bearbeiten]
Eine Funktion heißt streng konvex oder strikt konvex, wenn die Ungleichung der analytischen Definition im strengen Sinn gilt; das heißt, für alle Elemente aus und alle gilt, dass
- .
Eine Funktion heißt stark konvex mit Parameter bzw. -konvex, wenn für alle und gilt, dass
- .
Stark konvexe Funktionen sind auch strikt konvex, die Umkehrung gilt jedoch nicht.
Des Weiteren gibt es den Begriff der gleichmäßig konvexen Funktion, welcher das Konzept der starken Konvexität verallgemeinert. Eine Funktion heißt gleichmäßig konvex mit Módul , wobei wachsend ist und nur bei 0 verschwindet, wenn für alle und gilt[2]
- .
Wählt man mit , so erhält man die Ungleichung für starke Konvexität.
Für die Begriffe strikt konvex, stark konvex und gleichmäßig konvex lassen sich die entsprechenden Gegenstücke strikt konkav, stark konkav und gleichmäßig konkav definieren, indem die jeweiligen Ungleichungen umgedreht werden.
Beispiele[Bearbeiten | Quelltext bearbeiten]

- Lineare Funktionen sind auf ganz konvex und konkav, jedoch nicht streng.
- Die quadratische Funktion ist streng konvex.
- Die Funktion ist streng konvex.
- Die Funktion ist nicht konvex, da die Definitionsmenge keine konvexe Menge ist.
- Die Funktion ist streng konkav.
- Die Wurzelfunktion ist im Intervall streng konkav.
- Die Betragsfunktion ist konvex, jedoch nicht streng konvex.
- Die Exponentialfunktion ist streng konvex auf ganz .
- Der natürliche Logarithmus ist streng konkav auf dem Intervall der positiven reellen Zahlen.
- Die kubische Funktion ist streng konkav auf dem Intervall und streng konvex auf dem Intervall .
- Die Funktion, welche einen Punkt der euklidischen Ebene auf seinen Abstand vom Ursprung, abbildet, also
- ist ein Beispiel für eine konvexe Funktion auf einem mehrdimensionalen reellen Vektorraum.
Geschichte[Bearbeiten | Quelltext bearbeiten]
Wesentliche Aussagen zu konvexen und konkaven Funktionen finden sich bereits 1889 bei Otto Hölder, wobei er aber noch nicht die heute üblichen Bezeichnungen verwendete.[3] Die Begriffe konvexe und konkave Funktion wurden 1905 von Johan Ludwig Jensen eingeführt.[4] Jensen verwendete allerdings eine schwächere Definition, die noch gelegentlich, vor allem in älteren Werken,[5] zu finden ist. In dieser Definition wird nur die Ungleichung
vorausgesetzt. Wie Jensen aber zeigte, folgt daraus für stetige Funktionen die in der heute üblichen Definition verwendete Ungleichung
für alle zwischen 0 und 1.[6] (siehe auch: Abschnitt Konvexität und Stetigkeit)
Reellwertige Funktion, welche der oben genannten schwächeren Ungleichung () genügen, nennt man zu Ehren von Johan Ludwig Jensen Jensen-konvex oder kurz J-konvex.[7]
Elementare Eigenschaften[Bearbeiten | Quelltext bearbeiten]

Verhältnis konvex und konkav[Bearbeiten | Quelltext bearbeiten]
Die Funktion ist genau dann (streng) konvex, wenn die Funktion (streng) konkav ist. Eine nicht-konvexe Funktion muss jedoch nicht notwendigerweise konkav sein. Konvexität und Konkavität sind somit keine komplementären Eigenschaften.
Lineare Funktionen sind die einzigen Funktionen, die sowohl konkav als auch konvex sind.
- Beispiel
Die kubische Funktion ist auf ganz betrachtet weder konvex noch konkav. Im Intervall aller positiven reellen Zahlen ist streng konvex. Die zu ihr additiv inverse Funktion ist dort somit streng konkav.
Da eine ungerade Funktion ist, also gilt, folgt daraus, dass sie im Bereich aller negativen Zahlen streng konkav ist.
Niveaumengen[Bearbeiten | Quelltext bearbeiten]
Bei einer konvexen Funktion sind alle Subniveaumengen, also Mengen der Form
konvex. Bei einer konkaven Funktion sind alle Superniveaumengen konvex.
Jensensche Ungleichung[Bearbeiten | Quelltext bearbeiten]
Die Jensensche Ungleichung ist eine Verallgemeinerung der analytischen Definition auf eine endliche Anzahl von Stützstellen. Sie besagt, dass der Funktionswert einer konvexen Funktion an einer endlichen Konvexkombination von Stützstellen kleiner oder gleich der Konvexkombination von den Funktionswerten an den Stützstellen ist. Für eine konvexe Funktion und für nichtnegative mit gilt also:
Für konkave Funktionen gilt die Ungleichung in umgekehrter Richtung.
Reduktion auf Konvexität reeller Funktionen[Bearbeiten | Quelltext bearbeiten]
Der Urbildraum einer konvexen Funktion kann ein beliebiger reeller Vektorraum sein, wie zum Beispiel der Vektorraum der reellen Matrizen oder der stetigen Funktionen. Die Konvexität einer Funktion ist aber äquivalent zur Konvexität der Funktion definiert durch für alle , wobei ist und eine beliebige Richtung aus ist. Es ist dann . Dies macht es möglich, die Dimension des Vektorraumes zu verringern, was die Überprüfung der Konvexität erleichtert.
Ungleichungen für θ < 0 und θ > 1[Bearbeiten | Quelltext bearbeiten]
Für oder drehen sich die Ungleichungen aus den Definitionen von (strikter) Konvexität bzw. Konkavität um. Sei beispielsweise eine auf konvexe Funktion. Für Punkte und aus gilt dann
sofern auch der Punkt im Definitionsbereich liegt. Wenn eine reelle konvexe Funktion ist, bedeutet die Ungleichung anschaulich, dass die Funktionswerte von außerhalb des Intervalls stets oberhalb der Verbindungsgeraden durch die Funktionswerte liegen.
Rechenregeln[Bearbeiten | Quelltext bearbeiten]
Positivkombinationen[Bearbeiten | Quelltext bearbeiten]
Die Summe zweier (gegebenenfalls erweiterter) konvexer Funktionen ist wieder eine konvexe Funktion. Außerdem bleibt Konvexität beim Multiplizieren mit einer positiven reellen Zahl erhalten. Zusammenfassend gilt also, dass jede Positivkombination von konvexen Funktionen wiederum konvex ist. Sie ist sogar streng konvex, falls einer der auftretenden Summanden streng konvex ist. Analog dazu ist auch jede Positivkombination von konkaven Funktionen konkav. Somit bilden die konvexen Funktionen einen konvexen Kegel. Das Produkt konvexer Funktionen ist jedoch nicht notwendigerweise konvex.
- Beispiel
Die Funktionen
sind konvex auf ganz , die Normparabel ist sogar strikt konvex. Daraus folgt, dass auch alle Funktionen der Form
mit strikt konvex auf ganz sind. Dies ist auch anschaulich klar, es handelt sich um nach oben gekrümmte Parabeln. Das Produkt der Funktionen und ist die kubische Funktion , welche (über ganz betrachtet) nicht konvex ist.
Grenzfunktionen[Bearbeiten | Quelltext bearbeiten]
Die Grenzfunktion einer punktweise konvergenten Folge konvexer Funktionen ist eine konvexe Funktion. Ebenso ist die Grenzfunktion einer punktweise konvergenten Reihe konvexer Funktionen wieder eine konvexe Funktion. Analoges gilt klarerweise für konkave Funktionen. Strikte Konvexität bleibt unter der Grenzwertbildung jedoch nicht notwendigerweise erhalten, wie man anhand des ersten der beiden folgenden Beispiele erkennt.
- Beispiele
- Die Funktionenfolge mit ist eine Folge von auf ganz strikt konvexen Funktionen. Ihre punktweise Grenzfunktion ist die konstante Nullfunktion. Diese ist als lineare Funktion zwar konvex, aber nicht strikt konvex.
- Der Cosinus hyperbolicus lässt sich auf folgendermaßen als Potenzreihe entwickeln:
- Alle Summanden, die vorkommen, sind konvexe Funktionen. Daraus folgt, dass auch der Cosinus hyperbolicus eine konvexe Funktion ist.
Supremum und Infimum[Bearbeiten | Quelltext bearbeiten]
Ist eine Menge konvexer Funktionen und existiert punktweise das Supremum
für alle , so ist auch eine konvexe Funktion. Der Übergang zur Funktion zeigt, dass das Infimum einer Menge konkaver Funktionen (falls es existiert) ebenfalls wieder eine konkave Funktion ist. Das Bilden des Infimums erhält jedoch nicht notwendigerweise Konvexität (und umgekehrt erhält das Bilden des Supremums nicht notwendigerweise Konkavität), wie das folgende Beispiel zeigt.
- Beispiel
Die reellen Funktionen
sind linear und deshalb sowohl konvex als auch konkav. Das Supremum von und ist die Betragsfunktion . Diese ist zwar konvex, jedoch nicht konkav. Das Infimum von und ist die negative Betragsfunktion . Diese ist konkav, aber nicht konvex.
Komposition[Bearbeiten | Quelltext bearbeiten]
Über die Komposition zweier konvexer Funktionen und lässt sich im Allgemeinen keine Aussage treffen. Gilt jedoch zusätzlich, dass monoton steigend ist, so ist die Komposition ebenfalls konvex.
Des Weiteren ist die Komposition einer konkaven Funktion mit einer konvexen, monoton fallenden reellen Funktion wiederum eine konvexe Funktion.
- Beispiel
Jede Komposition einer konvexen Funktion mit der Exponentialfunktion liefert wieder eine konvexe Funktion. Dies funktioniert auch im allgemeinen Fall, in dem auf einem reellen Vektorraum definiert ist. So ist beispielsweise für
wiederum eine konvexe Funktion. Insbesondere ist also jede logarithmisch konvexe Funktion eine konvexe Funktion.
Umkehrfunktionen[Bearbeiten | Quelltext bearbeiten]
Ist eine auf einem Intervall definierte, invertierbare und konvexe Funktion, so folgt aus der Konvexitätsungleichung
Sei eine monoton steigende Funktion. Dann dreht sich obige Ungleichung beim Anwenden von um. Es gilt somit:
Also ist die Umkehrfunktion eine konkave (und monoton wachsende) Funktion. Für eine invertierbare, monoton steigende und konvexe bzw. konkave Funktion hat daher die Umkehrfunktion die umgekehrte Art der Konvexität.
Für eine monoton fallende und konvexe Funktion gilt hingegen
Für eine invertierbare monoton fallende und konvexe bzw. konkave Funktion hat daher die Umkehrfunktion die gleiche Art der Konvexität.
- Beispiele
- Die Normparabel ist monoton steigend und streng konvex auf . Ihre Umkehrfunktion, die Wurzelfunktion ist streng konkav auf ihrem Definitionsintervall
- Die Funktion ist monoton fallend und streng konvex auf ganz . Ihre Umkehrfunktion ist streng konvex auf dem Intervall
Extremwerte[Bearbeiten | Quelltext bearbeiten]

Wenn der Ausgangsraum einer konvexen/konkaven Funktion ein topologischer Vektorraum ist (was insbesondere auf alle endlichdimensionalen reellen Vektorräume und somit auch auf zutrifft), können Aussagen über das Verhältnis von lokalen und globalen Extremalstellen getroffen werden. Es gilt dann, dass jede lokale Extremalstelle auch eine globale Extremalstelle ist. Strikte Konvexität bzw. Konkavität erlaubt außerdem Aussagen über die Eindeutigkeit von Extremwerten.
Existenz und Eindeutigkeit[Bearbeiten | Quelltext bearbeiten]
Eine stetige konvexe oder konkave Funktion nimmt auf der kompakten Menge ein Minimum und ein Maximum an. Die Kompaktheit von ist auf äquivalent dazu, dass beschränkt und abgeschlossen ist. Dies ist der Satz vom Minimum und Maximum angewendet auf konvexe und konkave Funktionen. Ist die Funktion strikt konvex, so ist das Minimum eindeutig bestimmt, ist sie strikt konkav, so ist das Maximum eindeutig bestimmt. Der Umkehrschluss gilt jedoch nicht: die Funktion hat kein globales Minimum in , ist aber strikt konvex.
Für eine stetige Funktion auf einem reflexiven Banachraum gibt es analoge Aussagen: Ein stetiges konvexes Funktional auf der kompakten Menge nimmt dort ein Minimum an. Ist das Funktional strikt konvex, so ist das Minimum eindeutig.
Geometrie der Optimalwertmengen[Bearbeiten | Quelltext bearbeiten]
In topologischen Vektorräumen (welche fast immer gegeben sind) kann man auch lokale Minima untersuchen. Es gilt:
- Ist die Funktion konvex, so ist jedes lokale Minimum auch ein globales Minimum.
- Ist die Funktion konkav, so ist jedes lokale Maximum auch ein globales Maximum.
Dies lässt sich direkt mit den definierenden Ungleichungen von konvexen und konkaven Funktionen zeigen.
Außerdem ist die Menge der Minimalstellen einer konvexen Funktion konvex und die Menge der Maximalstellen einer konkaven Funktion konvex. Dies folgt aus der Konvexität der Subniveaumengen bzw. Superniveaumengen.
Kriterien für Extremwerte[Bearbeiten | Quelltext bearbeiten]
Für differenzierbare konvexe Funktionen nutzt man zur Bestimmung der Extremalwerte aus, dass konvexe Funktionen in jedem Punkt von der Tangente an diesem Punkt global unterschätzt werden. Es gilt , wobei das Standardskalarprodukt bezeichnet. Ist nun der Gradient in einem Punkt gleich null, so ist für alle und damit ist ein lokales (und damit globales) Minimum. Analog liegt bei konkaven Funktionen in einem Punkt immer ein lokales (und damit globales) Maximum vor, wenn der Gradient bzw. die Ableitung an diesem Punkt verschwindet.
Konvexität und Stetigkeit[Bearbeiten | Quelltext bearbeiten]
Setzt man die Stetigkeit einer reellen Funktion voraus, so reicht, um ihre Konvexität zu zeigen, bereits die Bedingung, dass für alle aus dem Definitionsintervall folgende Ungleichung gilt:
Dies entspricht der Konvexitätsdefinition nach Jensen. Umgekehrt gilt, dass jede auf einem Intervall definierte Funktion, die die obige Ungleichung erfüllt, in den inneren Punkten stetig ist. Unstetigkeitsstellen können höchstens in Randpunkten auftreten, wie das Beispiel der Funktion mit
zeigt, die zwar konvex ist, aber am Randpunkt eine Unstetigkeit aufweist.
Somit sind die beiden Möglichkeiten, Konvexität zu definieren, zumindest für offene Intervalle äquivalent. Inwiefern dieses Resultat auf allgemeine topologische Räume übertragen werden kann, wird in den beiden folgenden Abschnitten behandelt.
In diesem Zusammenhang ist der Satz von Bernstein-Doetsch zu erwähnen, aus dem allgemein das folgende Resultat zu gewinnen ist:[8]
- Ist eine reellwertige Funktion für eine konvexe offene Teilmenge des , so ist sowohl Jensen-konvex als auch stetig genau dann, wenn für je zwei Punkte und jede reelle Zahl stets die Ungleichung
- erfüllt ist.
Eine schwächere Definition der Konvexität[Bearbeiten | Quelltext bearbeiten]
Eine stetige Funktion auf einer konvexen Teilmenge eines reellen topologischen Vektorraums ist konvex, wenn ein festes mit existiert, sodass für alle , aus gilt:
Dies kann man mittels geeigneter Intervallschachtelung zeigen. Ein vollständig ausgeführter Beweis befindet sich im Beweisarchiv.
Dass in dieser schwächeren Definition von Konvexität Stetigkeit benötigt wird, lässt sich anhand des folgenden Gegenbeispiels erkennen.
- Gegenbeispiel
Sei eine Hamelbasis des Vektorraums der reellen Zahlen über dem Körper der rationalen Zahlen, also eine über den rationalen Zahlen linear unabhängige Menge reeller Zahlen, in der jede reelle Zahl eine eindeutige Darstellung der Art mit nur endlich vielen rationalen hat. Dann erfüllt bei beliebiger Wahl von die Funktion zwar ist aber nicht notwendigerweise konvex.
Beschränktheit und Stetigkeit in normierten Räumen[Bearbeiten | Quelltext bearbeiten]
Setzt man für eine Funktion zusätzlich zur Bedingung, dass für ein fixes die Beziehung
für alle , aus einer konvexen Teilmenge eines normierten Vektorraums gilt, noch voraus, dass nach oben beschränkt ist, so folgt daraus bereits die Stetigkeit von in den inneren Punkten von . Anschaulich wird dies daraus klar, dass man an einer Unstetigkeitsstelle eine beliebig steile Verbindungsgerade zwischen zwei Funktionswerten ziehen kann, wobei die Funktion zwischen den beiden Werten unterhalb der Verbindungsgeraden und außerhalb der beiden Werte oberhalb der Verbindungsgerade liegen muss. Kann die Verbindungsgerade nun beliebig steil werden, so stößt man irgendwann über die obere Schranke der Funktion.
Formal ist der Beweis allerdings etwas komplizierter. Eine vollständige Ausführung befindet sich im Beweisarchiv.
Die Aussage, dass eine konvexe beschränkte Funktion stetig in den inneren Punkten ist, ist auch bedeutsam für das Lösen der cauchyschen Funktionalgleichung
Aus dieser Aussage folgt nämlich, dass diese Funktionalgleichung eine eindeutige Lösung hat, wenn zusätzlich gefordert wird, dass beschränkt ist.
In endlichdimensionalen Räumen[Bearbeiten | Quelltext bearbeiten]
Konvexe Funktionen , die auf einer Teilmenge eines endlichdimensionalen reellen Vektorraums definiert sind, sind stetig in den inneren Punkten. Um das zu sehen, betrachte man einen inneren Punkt . Für diesen existiert ein Simplex mit den Eckpunkten , der wieder als inneren Punkt enthält. Jeder Punkt ist aber in der Form
- mit
und für alle darstellbar. Nach der jensenschen Ungleichung gilt nun
- .
ist daher nach oben beschränkt auf und somit, wie oben gezeigt wurde, stetig im inneren Punkt .
In unendlichdimensionalen Räumen[Bearbeiten | Quelltext bearbeiten]
Im unendlichdimensionalen Fall sind konvexe Funktionen nicht notwendigerweise stetig, da es insbesondere lineare (und somit auch konvexe) Funktionale gibt, die nicht stetig sind.
Konvexität und Differenzierbarkeit[Bearbeiten | Quelltext bearbeiten]
Konvexität und erste Ableitung[Bearbeiten | Quelltext bearbeiten]
Eine auf einem offenen Intervall definierte, konvexe bzw. konkave Funktion ist lokal Lipschitz-stetig und somit nach dem Satz von Rademacher fast überall differenzierbar. Sie ist in jedem Punkt links- und rechtsseitig differenzierbar.
Die Ableitung als Konvexitätskriterium[Bearbeiten | Quelltext bearbeiten]
Die erste Ableitung lässt sich auf zweierlei Arten als Konvexitätskriterium verwenden. Eine stetig differenzierbare reelle Funktion ist
- genau dann konvex auf , wenn ihre Ableitung dort monoton wachsend ist.
- genau dann streng konvex auf , wenn ihre Ableitung dort streng monoton wachsend ist.
- genau dann konkav auf , wenn ihre Ableitung dort monoton fallend ist.
- genau dann streng konkav auf , wenn ihre Ableitung dort streng monoton fallend ist.
Dieses Resultat findet sich im Wesentlichen schon 1889 bei Otto Hölder.[3] Mit dem erweiterten Monotoniebegriff für vektorwertige Funktionen lässt sich dies auch für Funktionen erweitern. Dann ist genau dann (strikt/gleichmäßig) konvex, wenn (strikt/gleichmäßig) monoton ist.
Alternativ ist eine differenzierbare Funktion genau dann
- konvex, wenn ist für alle .
- strikt konvex, wenn ist für alle .
- konkav, wenn ist für alle .
- strikt konkav, wenn ist für alle .
Im Falle einer Funktion vereinfacht sich zu .
Beispiel[Bearbeiten | Quelltext bearbeiten]
Betrachtet man als Beispiel den Logarithmus . Er ist auf dem Intervall stetig differenzierbar mit Ableitung .
Nach dem ersten Konvexitätskriterium muss jetzt die Ableitung auf Monotonie untersucht werden. Ist und , so ist , da Zähler und Nenner echt positiv sind. Somit ist streng monoton fallend und folglich ist streng konkav auf .
Nach dem zweiten Monotoniekriterium überprüft man für
- .
Da aber für ist, gilt die Ungleichung, wenn ist und sind. Also ist der Logarithmus streng konkav auf .
Betrachtet man die Funktion
- ,
so sind alle partiellen Ableitungen stetig und für den Gradient gilt
Zur Überprüfung des ersten Konvexitätskriteriums bildet man für
- ,
da die quadratischen Terme immer echt positiv sind, die Positivität der Terme mit folgt aus der Monotonie der e-Funktion. Somit ist die Funktion strikt monoton, also auch strikt konvex.
Tangenten[Bearbeiten | Quelltext bearbeiten]
Die Graphen differenzierbarer konvexer Funktionen liegen oberhalb jeder ihrer Tangenten. Analog dazu liegen konkave Funktionen stets unterhalb ihrer Tangenten. Dies folgt direkt aus dem zweiten Konvexitätskriterium. Dieses lässt sich auch so interpretieren, dass die Taylor-Entwicklung ersten Grades eine konvexe Funktion stets global unterschätzt. Aus diesen Eigenschaften folgt beispielsweise die Verallgemeinerung der bernoullischen Ungleichung:
- für oder
- für .
Konvexität und zweite Ableitung[Bearbeiten | Quelltext bearbeiten]
Konvexitätskriterien und zweimalige Differenzierbarkeit[Bearbeiten | Quelltext bearbeiten]
Für eine zweimal differenzierbare Funktion lassen sich weitere Aussagen treffen. ist genau dann konvex, wenn ihre zweite Ableitung nicht negativ ist. Ist durchweg positiv, also stets linksgekrümmt, dann folgt daraus, dass streng konvex ist. Analog dazu ist genau dann konkav, wenn gilt. Ist durchweg negativ, also stets rechtsgekrümmt, so ist streng konkav.
Ist die mehrdimensionale Funktion zweimal stetig differenzierbar, dann gilt, dass genau dann konvex ist, wenn die Hesse-Matrix von positiv semidefinit ist. Ist die Hesse-Matrix von positiv definit, so ist strikt konvex. Umgekehrt ist genau dann konkav, wenn die Hesse-Matrix von negativ semidefinit ist. Ist die Hesse-Matrix von negativ definit, so ist strikt konkav.
Im Kern basieren die Konvexitätskriterien zweiter Ordnung auf der Überprüfung der Monotonie der Ableitung durch Monotoniekriterien, die wiederum auf Differenzierbarkeit basieren.
Beispiele[Bearbeiten | Quelltext bearbeiten]
Die Funktion mit ist konvex, da für alle . Sie ist sogar streng konvex, was beweist, dass strenge Konvexität nicht impliziert, dass die zweite Ableitung positiv ist ( hat bei 0 eine Nullstelle).
Die oben betrachtete Funktion ist zweimal stetig differenzierbar auf mit zweiter Ableitung für alle . Also ist die Funktion streng konkav.
Betrachtet man die Funktion
- ,
so ist ihre Hesse-Matrix
- .
Sie ist positiv definit, da alle ihre Eigenwerte echt positiv sind. Also ist strikt konvex.
Konvexe Funktionen in der Geometrie[Bearbeiten | Quelltext bearbeiten]
Eine nicht-leere, abgeschlossene Teilmenge eines reellen normierten Vektorraums ist genau dann konvex, wenn die durch
definierte Abstandsfunktion eine konvexe Funktion ist.
Dieselbe Eigenschaft gilt nicht nur für Teilmengen des , sondern auch allgemein für Teilmengen von CAT(0)-Räumen, insbesondere von Riemannschen Mannigfaltigkeit nichtpositiver Schnittkrümmung. Die Konvexität der Abstandsfunktion ist ein wichtiges Hilfsmittel bei der Untersuchung nichtpositiv gekrümmter Räume.[9]
Verallgemeinerungen[Bearbeiten | Quelltext bearbeiten]
Für reellwertige Funktionen[Bearbeiten | Quelltext bearbeiten]
- Eine quasikonvexe Funktion verallgemeinert die Eigenschaft einer konvexen Funktion, dass ihre Subniveaumengen, also Mengen der Form
- ,
- konvex sind. Eine Funktion ist quasikonvex, wenn jede Subniveaumenge konvex ist. Jede konvexe Funktion ist quasikonvex, die Umkehrung gilt nicht.
- Eine pseudokonvexe Funktion ist eine differenzierbare Funktion, für die gilt: Wenn gilt, so folgt . Diese Funktionen verallgemeinern die Eigenschaft konvexer Funktionen, dass an einer Stelle mit verschwindendem Gradienten ein globales Minimum vorliegt. Jede differenzierbare konvexe Funktion ist pseudokonvex.
- Logarithmische Konvexität einer Funktion liegt vor, wenn konvex ist. Streng genommen sind logarithmisch konvexe Funktionen keine Verallgemeinerung, sondern ein Spezialfall von konvexen Funktionen.
Für Funktionen in endlichdimensionalen Vektorräumen[Bearbeiten | Quelltext bearbeiten]
- K-konvexe Funktionen verallgemeinern konvexität von Funktionen, die nach abbilden, auf den Fall, dass die Funktion in den abbildet, also vektorwertig ist. Dies geschieht mittels verallgemeinerter Ungleichungen.
- Ein Spezialfall von K-konvexen Funktionen sind die Matrix-konvexen Funktionen. Sie bilden in den Raum der reellen symmetrischen Matrizen, versehen mit der Loewner-Halbordnung, ab.
Für Abbildungen in allgemeinen reellen Vektorräumen[Bearbeiten | Quelltext bearbeiten]
- Die fast konvexen Funktionen verallgemeinern die Konvexität so, dass für sie möglichst gute Regularitätsvoraussetzungen in der Optimierung gelten.
- Eine konvexe Abbildung ist eine Abbildung zwischen zwei reellen Vektorräumen, für die
- für alle und aus der konvexen Menge gilt. Hierbei ist ein Ordnungskegel auf .
Im Bezug auf Referenzsysteme[Bearbeiten | Quelltext bearbeiten]
- Verallgemeinerte Konvexität definiert die Konvexität einer Funktion im Bezug auf eine Menge von Abbildungen, das sogenannte Referenzsystem.
Siehe auch[Bearbeiten | Quelltext bearbeiten]
Literatur[Bearbeiten | Quelltext bearbeiten]
- Stephen Boyd, Lieven Vandenberghe: Convex Optimization. Cambridge University Press, Cambridge, New York, Melbourne 2004, ISBN 0-521-83378-7 (stanford.edu).
- Peter Kosmol: Optimierung und Approximation (= De Gruyter Studium). 2. Auflage. Walter de Gruyter & Co., Berlin 2010, ISBN 978-3-11-021814-5 (MR2599674).
- Marek Kuczma: An Introduction to the Theory of Functional Equations and Inequalities. Cauchy's Equation and Jensen's Inequality. 2. Auflage. Birkhäuser Verlag, Basel 2009, ISBN 978-3-7643-8748-8 (MR2467621).
- Kurt Leichtweiß: Konvexe Mengen (= Hochschultext). Springer-Verlag, Berlin, Heidelberg, New York 1980, ISBN 3-540-09071-1 (MR0586235).
- Jürg T. Marti: Konvexe Analysis (= Lehrbücher und Monographien aus dem Gebiet der Exakten Wissenschaften, Mathematische Reihe. Band 54). Birkhäuser Verlag, Basel, Stuttgart 1977, ISBN 3-7643-0839-7 (MR0511737).
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Convex Function in Mathworld
- Concave Function in Mathworld
- Convex Function in PlanetMath, Archivlink abgerufen am 24. Dezember 2022
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Ralph Tyrell Rockafellar: Convex Analysis. Princeton University Press, Princeton 1970, ISBN 1-4008-7317-7, Section 4.
- ↑ Heinz H. Bauschke, Patrick L. Combettes: Convex Analysis and Monotone Operator Theory in Hilbert Spaces. In: CMS Books in Mathematics. 2011, ISSN 1613-5237, doi:10.1007/978-1-4419-9467-7.
- ↑ a b Otto Hölder: Ueber einen Mittelwerthssatz. In: Nachrichten von der Königl. Gesellschaft der Wissenschaften und der Georg-Augusts-Universität zu Göttingen. Aus dem Jahre 1889., Nr. 1-21. Dieterichsche Verlags-Buchhandlung, Göttingen 1889, S. 38 ff. (in Wikisource [abgerufen am 24. März 2012]).
- ↑ Earliest Known Uses of Some of the Words of Mathematics, 28. Juli 2006: A. Guerraggio and E. Molho write, „The first modern formalization of the concept of convex function appears in J. L. W. V. Jensen Om konvexe funktioner og uligheder mellem midelvaerdier, Nyt Tidsskr. Math. B 16 (1905), S. 49–69. Since then, at first referring to Jensen’s convex functions, then more openly, without needing any explicit reference, the definition of convex function becomes a standard element in calculus handbooks.“ („The Origins of Quasi-concavity: a Development between Mathematics and Economics“, Historia Mathematica, 31, (2004), 62–75.)
- ↑ z. B. in I. P. Natanson: Theorie der Funktionen einer reellen Veränderlichen, 4. Auflage, Verlag Harri Deutsch, Thun, 1981, ISBN 3-87144-217-8.
- ↑ Jensen, J. L. W. V.: Sur les fonctions convexes et les inégalités entre les valeurs moyennes. In Acta Math. 30, 175–193, 1906.
- ↑ Marek Kuczma: An Introduction to the Theory of Functional Equations and Inequalities. 2009, S. 130 (Fußnote)
- ↑ Kuczma. op. cit., S. 161–162
- ↑ Ballmann, Werner; Gromov, Mikhael; Schroeder, Viktor: Manifolds of nonpositive curvature. Progress in Mathematics, 61. Birkhäuser Boston, Inc., Boston, MA, 1985. ISBN 0-8176-3181-X





![{\displaystyle \theta \in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fead1e7dceab4be5ab2e91f5108144722daa8c36)















































![{\displaystyle \forall x,y\in C,\ \theta \in [0,1]:\quad f(\theta x+(1-\theta )y)\geq \theta f(x)+(1-\theta )f(y),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93e60e526141dc5f2ef785c2f802dfb5ce355182)







![{\displaystyle \phi \colon [0,\infty )\to [0,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97eb895ae471ed1997d4fc15dc7ddca05bbdec85)


















































































![{\displaystyle t\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31a5c18739ff04858eecc8fec2f53912c348e0e5)







































































![{\displaystyle \lambda \in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/010c0ee88963a09590dd07393d288edd83786b91)


