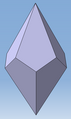
Trapezoeder

Ein Trapezoeder ist ein Polyeder, das von deckungsgleichen „schiefen“ Vierecken begrenzt ist – also von solchen, bei denen keine Seite einer anderen parallel ist (Trapezoide oder Trapeze im älteren Sinn.[1]) Ein Trapezoeder kann man sich als eine Bipyramide vorstellen, bei der die obere gegen die untere Pyramide um einen beliebigen Winkel verdreht ist. Ein Trapezoeder wird n-gonal genannt, wobei n die Hälfte der Anzahl seiner Flächen ist. (Zwei sich berührende Kanten der Vierecke haben notwendigerweise die gleiche Länge.)
Trapezoeder kommen in der Natur als Kristallform vor: Sie sind die allgemeine Flächenform der enantiomorphen Kristallklassen 32 (trigonal-trapezoedrische), 422 (tetragonal-trapezoedrische) und 622 (hexagonal-trapezoedrische Klasse).
Symmetrie[Bearbeiten | Quelltext bearbeiten]
Trapezoeder sind punktsymmetrisch. Der Symmetriepunkt ist der Schnittpunkt der Raumdiagonalen. Eine der Raumdiagonalen stellt eine n-zählige Drehachse dar.
Trapezoeder mit höherer Symmetrie[Bearbeiten | Quelltext bearbeiten]
Ein Trapezoeder mit höherer Symmetrie entsteht, wenn die Flächen der oberen Pyramide genau in der Mitte zwischen denen der unteren liegen. Der Winkel der Verdrehung ist dann 180°/m bei einer m-zähligen Pyramide. Die Flächen solcher Körper sind Drachenvierecke („Deltoide“). Diese höhersymmetrischen Trapezoeder werden auch Deltoeder oder Antipyramide genannt; ihre dualen Polyeder sind gerade Antiprismen.
-
trigonales Trapezoeder
-
tetragonales Trapezoeder
-
Pentagonales Trapezoeder
-
pentagonales Trapezoeder als zehnseitiger Spielwürfel
-
hexagonales Trapezoeder
Deltoidalikositetraeder[Bearbeiten | Quelltext bearbeiten]
Daneben wird gelegentlich auch das kubische Deltoidalikositetraeder, ein Körper mit 24 drachenförmigen Flächen, Trapezoeder genannt.
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Brockhaus’ Kleines Konversations-Lexikon. 5. Aufl. 1911, Artikel „Trapez“.
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Eric W. Weisstein: Trapezohedron. In: MathWorld (englisch).