Eulersche Winkel

Die eulerschen Winkel (oder Euler-Winkel), benannt nach dem Schweizer Mathematiker Leonhard Euler, sind ein Satz dreier unabhängiger Parameter, mit denen die Orientierung (Drehlage) eines festen Körpers im dreidimensionalen Raum beschrieben werden kann. Die Drehlage wird aus einer beliebigen anderen durch eine Abfolge dreier Drehungen um spezielle Achsen erzeugt, wobei die Drehwinkel die unabhängigen Parameter sind. Die erste Drehachse ist eine raumfeste, die beiden anderen sind vorher mitgedrehte Achsen. Die Drehungen des Körpers (aktive Drehungen) stellen eine geometrische Transformation dar.

Im Besonderen dienen eulersche Winkel dazu, um mit ihnen eine Koordinatentransformation durchzuführen. Die in einem kartesischen Koordinatensystem bekannten Koordinaten eines zu einem Körperpunkt führenden Ortsvektors werden in die zu einem anderen kartesischen Koordinatensystem, das zum ersten im Ursprungspunkt verdreht (passive Drehungen) ist, gehörenden Koordinaten umgerechnet. Gängige Bezeichnungen der beiden Koordinatensysteme sind raumfestes oder Labor-System und körperfestes oder Körper-System.

aktive Drehung:
Drehung eines Körpers als Folge von drei einzelnen Drehungen um seine Körperachsen z,x',z" (eigenes Koordinatensystem: rot)
festes Referenzsystem:blau

Drehungen/Transformationen und Drehmatrizen

Die Transformationen werden mit Hilfe von Drehmatrizen, deren Elemente Sinus- und Cosinus-Werte der Euler-Winkel sind, berechnet.

Koordinatentransformation (passive Drehungen)

Die Drehmatrix für die Koordinatentransformation sei  $M.$ Die körpereigenen XYZ-Koordinaten eines Ortsvektors zu einem Körperpunkt errechnen sich aus seinen raumfesten xyz-Koordinaten mit folgender Multiplikation.

${\begin{aligned}{\begin{pmatrix}X\\Y\\Z\\\end{pmatrix}}&=M{\begin{pmatrix}x\\y\\z\\\end{pmatrix}}\end{aligned}}.$

Der Vektor (Körper) bleibt am Ort. Das Koordinatensystem wird vordergründig mathematisch positiv gedreht.

Die transponierte Drehmatrix  $M^{T}$  drückt den umgekehrten Vorgang aus:

${\begin{aligned}{\begin{pmatrix}x\\y\\z\\\end{pmatrix}}&=M^{T}{\begin{pmatrix}X\\Y\\Z\\\end{pmatrix}}\end{aligned}}.$

Der Vektor (Körper) bleibt am Ort. Das Koordinatensystem wird vordergründig zurück gedreht (tatsächlich Übergang von altem zu neuem Koordinatensystem).

Geometrische Transformation (aktive Drehungen)

Die transponierte Drehmatrix  $M^{T}$  beschreibt auch die Drehung des Vektors (Körpers, geometrische Transformation).

Dabei bleibt das alte Koordinatensystem am Ort. Der Körper (Vektor) wird zusammen mit dem körpereigenen Koordinatensystem mathematisch negativ gedreht.

Drehfolge-Kombinationen

Euler-Winkel werden nicht für Drehungen um raumfeste Achsen, sondern immer für Drehungen um Achsen desjenigen Koordinatensystems angewendet, das schlussendlich das gedrehte System ist.

Es gibt sechs verschiedene Kombinationen für drei aufeinander folgende Drehungen um drei verschiedene Achsen. Sie bilden die Gruppe der sogenannten Tait-Bryan-Drehungen beziehungsweise Tait-Bryan-Winkel oder auch Kardanwinkel.

Da zwei Achsen bei der Drehung um die dritte Achse ihre Richtung ändern, darf die dritte Drehung wieder um die erste Achse mit neuer Richtung erfolgen. Das ergibt sechs weitere Drehfolgen, die als klassische oder reine Drehfolgen mit Euler-Winkeln bezeichnet werden. Von diesen werden die zwei im Folgenden näher vorgestellten vorzugsweise verwendet und als sogenannte Standardkonventionen bezeichnet.

KoordinatenTransformation, Drehfolge in Standard-„x-Konvention“
blau: Koordinatensystem in Ausgangslage
grün: Schnittgerade der xy-Ebenen, Zwischenlage der x-Achse
rot: Koordinatensystem in Ziellage

Standard-x-Konvention (z, x′, z″)

Zuerst wird mit dem Winkel $\alpha$ um die $z$-Achse des Koordinatensystems in Ausgangslage gedreht (Kurzzeichen z). Es folgt eine Drehung mit dem Winkel $\beta$ um die $x$-Achse in deren Lage nach der ersten Drehung (Kurzzeichen x′) und schließlich eine Drehung mit dem Winkel $\gamma$ um die $z$-Achse in deren Lage nach den beiden vorherigen Drehungen (Kurzzeichen z″).

${\begin{aligned}M_{zxz}&={\begin{pmatrix}\cos \gamma &\sin \gamma &0\\-\sin \gamma &\cos \gamma &0\\0&0&1\end{pmatrix}}{\begin{pmatrix}1&0&0\\0&\cos \beta &\sin \beta \\0&-\sin \beta &\cos \beta \end{pmatrix}}{\begin{pmatrix}\cos \alpha &\sin \alpha &0\\-\sin \alpha &\cos \alpha &0\\0&0&1\end{pmatrix}}\\M_{zxz}&={\begin{pmatrix}\cos \alpha \cos \gamma -\sin \alpha \cos \beta \sin \gamma &\sin \alpha \cos \gamma +\cos \alpha \cos \beta \sin \gamma &\sin \beta \sin \gamma \\-\cos \alpha \sin \gamma -\sin \alpha \cos \beta \cos \gamma &-\sin \alpha \sin \gamma +\cos \alpha \cos \beta \cos \gamma &\sin \beta \cos \gamma \\\sin \alpha \sin \beta &-\cos \alpha \sin \beta &\cos \beta \end{pmatrix}}\end{aligned}}$

Die Teilmatrizen beschreiben je eine Drehung um eine Achse.
Die Zeilen von $M_{zxz}$ bestehen aus den im Ausgangssystem xyz angegebenen Koordinaten der drei Einheitsvektoren des Zielsystems XYZ.

Die transponierte Matrix $M_{zxz}^{T}$ wird durch Vertauschen von Zeilen und Spalten in der Matrix $M_{zxz}$ ermittelt.

${\begin{aligned}M_{zxz}^{T}&={\begin{pmatrix}\cos \alpha \cos \gamma -\sin \alpha \cos \beta \sin \gamma &-\cos \alpha \sin \gamma -\sin \alpha \cos \beta \cos \gamma &\sin \alpha \sin \beta \\\sin \alpha \cos \gamma +\cos \alpha \cos \beta \sin \gamma &-\sin \alpha \sin \gamma +\cos \alpha \cos \beta \cos \gamma &-\cos \alpha \sin \beta \\\sin \beta \sin \gamma &\sin \beta \cos \gamma &\cos \beta \\\end{pmatrix}}\end{aligned}}$

• 
  α: Drehung um z-Achse
• 
  β: Drehung um x′-Achse
• 
  γ: Drehung um z″-Achse

Standard-y-Konvention (z, y′, z″)

Zuerst wird um den Winkel $\alpha$ um die $z$-Achse des Koordinatensystems in Ausgangslage gedreht (Kurzzeichen z). Es folgt eine Drehung um den Winkel $\beta$ um die $y$-Achse in deren Lage nach der ersten Drehung (Kurzzeichen y′) und schließlich eine Drehung um den Winkel $\gamma$ um die $z$-Achse in deren Lage nach den beiden vorherigen Drehungen (Kurzzeichen z″).

${\begin{aligned}M_{zyz}&={\begin{pmatrix}\cos \gamma &\sin \gamma &0\\-\sin \gamma &\cos \gamma &0\\0&0&1\end{pmatrix}}{\begin{pmatrix}\cos \beta &0&-\sin \beta \\0&1&0\\\sin \beta &0&\cos \beta \end{pmatrix}}{\begin{pmatrix}\cos \alpha &\sin \alpha &0\\-\sin \alpha &\cos \alpha &0\\0&0&1\end{pmatrix}}\\\end{aligned}}$

${\begin{aligned}M_{zyz}&={\begin{pmatrix}-\sin \alpha \sin \gamma +\cos \alpha \cos \beta \cos \gamma &\cos \alpha \sin \gamma +\sin \alpha \cos \beta \cos \gamma &-\sin \beta \cos \gamma \\-\sin \alpha \cos \gamma -\cos \alpha \cos \beta \sin \gamma &\cos \alpha \cos \gamma -\sin \alpha \cos \beta \sin \gamma &\sin \beta \sin \gamma \\\cos \alpha \sin \beta &\sin \alpha \sin \beta &\cos \beta \end{pmatrix}}\end{aligned}}$

${\begin{aligned}M_{zyz}^{T}&={\begin{pmatrix}-\sin \alpha \sin \gamma +\cos \alpha \cos \beta \cos \gamma &-\sin \alpha \cos \gamma -\cos \alpha \cos \beta \sin \gamma &\cos \alpha \sin \beta \\\cos \alpha \sin \gamma +\sin \alpha \cos \beta \cos \gamma &\cos \alpha \cos \gamma -\sin \alpha \cos \beta \sin \gamma &\sin \alpha \sin \beta \\-\sin \beta \cos \gamma &\sin \beta \sin \gamma &\cos \beta \end{pmatrix}}\end{aligned}}$

• 
  α: Drehung um z-Achse
• 
  β: Drehung um y′-Achse
• 
  γ: Drehung um z″-Achse

Drehfolgen in der Fahrzeugtechnik

Koordinatentransformation in der Flugtechnik, Drehfolge z, y′, x″ (Gier-Nick-Roll)
blau: raumfestes Koordinatensystem (Ausgangslage)
grün: Zwischenlage der y-Achse (Knotenachse N(y′))
rot: körperfestes Koordinatensystem (Ziellage)
Anmerkung: z-Achse zeigt in Praxis der Flugtechnik nach unten zur Erde (s. nächstes Bild)

Gier-, Nick- und Rollwinkel$(\Psi ,\Theta ,\Phi )$ als Lagewinkel eines Flugzeugs
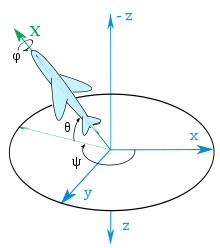
Gier- und Nickwinkel gegenüber erdfestem System,
Rollwinkel gegenüber Flugzeug-Längsachse

Die in der Fahrzeugtechnik angewendeten und genormten (Luftfahrt: DIN 9300; Automobilbau: DIN 70000 (mittlerweile DIN 8855); Schifffahrt) Drehfolgen gehören in die Gruppe der Tait-Bryan-Drehungen (Drehung um die drei Koordinatenachsen). In den Normen sind die Verwendung der Formelzeichen $\Psi$, $\Theta$ und $\Phi$ (Psi, Theta, Phi) und die Namen Gier-, Nick- und Roll-Winkel (engl. yaw, pitch and roll angle) für die drei Euler-Winkel vorgeschrieben. Durch die drei Drehungen wird das erdfeste System (engl. world frame) xyz in das körperfeste Koordinatensystem (engl. body frame) XYZ oder umgekehrt gedreht.

Gier-Nick-Roll: X-Y'-Z''-Konvention(S. 72)

Die Drehfolge ist:

• Mit dem im erdfesten System gemessenen Gierwinkel $\Psi$ (auch Steuerkurs oder Azimut genannt) wird um die $z$-Achse gedreht. Die $y$-Achse wird zur Knotenachse $N(y')$.
  Hauptwertebereich: $-\pi <\Psi \leq \pi$
• Mit dem gegen die Erdoberfläche ($x$-$y$-Ebene) gemessenen Nickwinkel $\Theta$ wird um die Knotenachse $N(y')$ gedreht. Es entsteht die fahrzeugfeste $X$-Achse.
  Hauptwertebereich: $-{\frac {\pi }{2}}\leq \Theta \leq {\frac {\pi }{2}}$
• Der Rollwinkel $\Phi$ (auch Wankwinkel genannt) beschreibt die Drehung um die fahrzeugfeste $X$-Achse. Es entstehen die fahrzeugfesten Achsen $Y$ und $Z$.
  Hauptwertebereich: $-\pi <\Phi \leq \pi$

${\begin{aligned}M_{GNR}&={\begin{pmatrix}1&0&0\\0&\cos \Phi &\sin \Phi \\0&-\sin \Phi &\cos \Phi \end{pmatrix}}{\begin{pmatrix}\cos \Theta &0&-\sin \Theta \\0&1&0\\\sin \Theta &0&\cos \Theta \end{pmatrix}}{\begin{pmatrix}\cos \Psi &\sin \Psi &0\\-\sin \Psi &\cos \Psi &0\\0&0&1\end{pmatrix}}\end{aligned}}$

${\begin{aligned}M_{GNR}&={\begin{pmatrix}\cos \Theta \cos \Psi &\cos \Theta \sin \Psi &-\sin \Theta \\\sin \Phi \sin \Theta \cos \Psi -\cos \Phi \sin \Psi &\sin \Phi \sin \Theta \sin \Psi +\cos \Phi \cos \Psi &\sin \Phi \cos \Theta \\\cos \Phi \sin \Theta \cos \Psi +\sin \Phi \sin \Psi &\cos \Phi \sin \Theta \sin \Psi -\sin \Phi \cos \Psi &\cos \Phi \cos \Theta \end{pmatrix}}\end{aligned}}$

• 
  Ψ: Drehung um z-Achse
• 
  Θ: Drehung um y′-Achse
• 
  Φ: Drehung um x″-Achse

Anwendungsbeispiel

Der Gewichtsvektor G_E hat im erdfesten Koordinatensystem xyz nur eine z-Komponente (in Richtung Erdmittelpunkt):

$G_{E}={\begin{pmatrix}0\\0\\mg\end{pmatrix}}$

Die Transformation ins flugzeugfeste Koordinatensystem geschieht dann durch Linksmultiplikation des erdfesten Gewichtsvektors $G_{E}$ mit der Transformationsmatrix $M_{GNR}$:

${\begin{aligned}G_{F}&=M_{GNR}G_{E}\\&={\begin{pmatrix}\cos \Theta \cos \Psi &\cos \Theta \sin \Psi &-\sin \Theta \\\sin \Phi \sin \Theta \cos \Psi -\cos \Phi \sin \Psi &\sin \Phi \sin \Theta \sin \Psi +\cos \Phi \cos \Psi &\sin \Phi \cos \Theta \\\cos \Phi \sin \Theta \cos \Psi +\sin \Phi \sin \Psi &\cos \Phi \sin \Theta \sin \Psi -\sin \Phi \cos \Psi &\cos \Phi \cos \Theta \end{pmatrix}}{\begin{pmatrix}0\\0\\mg\end{pmatrix}}\\&={\begin{pmatrix}\ldots &\ldots &-\sin \Theta \\\ldots &\ldots &\sin \Phi \cos \Theta \\\ldots &\ldots &\cos \Phi \cos \Theta \end{pmatrix}}{\begin{pmatrix}0\\0\\mg\end{pmatrix}}\\&={\begin{pmatrix}-\sin \Theta \\\sin \Phi \cos \Theta \\\cos \Phi \cos \Theta \end{pmatrix}}mg\end{aligned}}$

Physikalisch richtig wirkt das Gewicht G_E bei vorhandenem Nickwinkel $\Theta$ im Flugzeug beispielsweise auch nach hinten (in negative $X$-Richtung).

Roll-Nick-Gier: x, y′, z″-Konvention

Mit Hilfe der transponierten Drehmatrix $M_{GNR}^{T}$ = $M_{RNG}$ können die im Flugzeug gemessenen, auf das bordeigene Koordinatensystem bezogenen vektoriellen Größen (z. B. Beschleunigungen) in ein erdfestes Koordinatensystem umgerechnet werden.

${\begin{aligned}M_{GNR}^{T}=M_{RNG}&={\begin{pmatrix}\cos \Theta \cos \Psi &\sin \Phi \sin \Theta \cos \Psi -\cos \Phi \sin \Psi &\cos \Phi \sin \Theta \cos \Psi +\sin \Phi \sin \Psi \\\cos \Theta \sin \Psi &\sin \Phi \sin \Theta \sin \Psi +\cos \Phi \cos \Psi &\cos \Phi \sin \Theta \sin \Psi -\sin \Phi \cos \Psi \\-\sin \Theta &\sin \Phi \cos \Theta &\cos \Phi \cos \Theta \end{pmatrix}}\end{aligned}}$

Matrix-Herleitung im allgemeinen Fall

Für eine beliebige Wahl der Drehachsenreihenfolge kann die sich ergebende Drehmatrix durch die Zuhilfenahme des folgenden Zusammenhangs einfach hergeleitet werden:

Die Drehmatrizen um die globalen Achsen sind bekannt. Wenn nun um eine bereits gedrehte Achse erneut gedreht werden soll, dann entspricht das der Drehmatrix um die entsprechende globale Achse, allerdings in einer transformierten Vektorbasis. Die Transformationsmatrix (Basiswechselmatrix) ist dabei gerade die vorhergehende Drehung.

Seien $A$ und $B$ zwei Drehmatrizen um die beiden globalen Achsen $G$ und $H$. Zur Berechnung der Drehmatrix zu der Reihenfolge $(G,H^{\prime })$ beobachtet man, dass die Drehmatrix für die zweite Drehung um $H$ der basistransformierten Matrix ${\tilde {B}}=ABA^{-1}$ entsprechen muss. Dadurch erhält man für die resultierende Gesamtdrehmatrix $C={\tilde {B}}A=ABA^{-1}A=AB$. Für eine größere Anzahl von Drehungen erfolgt der Nachweis analog.

Durch diese Darstellung ergibt sich, dass sich die Drehmatrix für eine beliebige Drehreihenfolge in nacheinander gedrehten Achsen durch die einfache Multiplikation von Drehmatrizen um globale Koordinatenachsen ergibt – allerdings in umgekehrter Reihenfolge.

Ergebnis, Interpretation

Das erhaltene Koordinatensystem mit den Achsen $X''$, $Y''$ und $Z''$ ist das sogenannte körperfeste System. Die Winkel $\phi$ und $\theta$ geben dabei die Lage der $Z''$-Achse gegenüber dem körperfesten System an („Drehung“ und „Kippung“); der Winkel $\psi$ beschreibt die Eigendrehung des Körpers um sie. Dem entsprechen folgende Namenskonventionen:

• Flugsteuerung (Rollwinkel, Nickwinkel, Gierwinkel)
• Kreiseltheorie: Präzession, Nutation und Spin oder Eigenrotation
• Azimut, Höhenwinkel oder Elevation und Rotation

Mathematische Eigenschaften

Die Abbildung, die den Euler-Winkeln die zugehörige Drehmatrix zuordnet, besitzt kritische Punkte, in denen diese Zuordnung nicht lokal umkehrbar ist und man von einer kardanischen Blockade (englisch gimbal lock) spricht. Im Fall der og. x- oder y-Konvention tritt dieser stets dann auf, wenn der zweite Rotationswinkel gleich null wird und der Drehvektor der ersten Drehung damit derselbe ist wie der Drehvektor der zweiten Drehung. Das aber bedeutet, dass es für eine Rotation um die $z$-Achse beliebig viele Euler-Winkel mit $\alpha =Z+Z'$ gibt.

Bei der Definition der Lagewinkel nach der Luftfahrtnorm liegen die kritischen Punkte bei $\textstyle \Theta =\pm {\frac {\pi }{2}}$.

Nachteile, Alternativen

Zur Darstellung von Drehungen haben Euler-Winkel mehrere Nachteile:

• Die oben erwähnte Singularität führt dazu, dass eine einzige Drehung durch unterschiedliche Euler-Drehungen ausgedrückt werden kann. Dies führt zu einem Phänomen, das als Gimbal Lock bekannt ist.
• Die korrekte Kombination von Drehungen im Euler-System ist nicht intuitiv anzugeben, da sich die Drehachsen verändern.

Eine andere Möglichkeit, die Orientierung zu beschreiben und teils diese Nachteile zu umgehen, sind Quaternionen.

Anwendungen

Textur Polfiguren von gamma-TiAl in einer alpha2-gamma Zweiphasenlegierung.

Roll-Nick-Gier-Winkel (Eulerwinkel)
0 Rotationsachsen:	Bewegung:
↙ Längsachse (Roll-/Wankachse):	Rollen, Wanken
↖ Querachse (Nickachse):	Nicken, Stampfen
↓ Vertikalachse (Gierachse):	Gieren (Schlingern)

In der Theoretischen Physik werden die eulerschen Winkel zur Beschreibung des Starren Körpers benutzt. Eine praktische Anwendung ergibt die bekannte kardanische Aufhängung der technischen Mechanik.

Bei Fahrzeugen bezeichnet man die Euler-Winkel der Hauptlagen als Roll-Nick-Gier-Winkel.

In der Kristallographie werden die eulerschen Winkel zur Beschreibung der Kreise des Einkristalldiffraktometers (mit einer kardanischen Aufhängung aus zwei senkrecht aufeinander stehenden Drehkreisen, die den Euler-Winkeln entspricht und Euler-Wiege genannt wird) und zur Beschreibung der Orientierungsdichteverteilungsfunktion von Texturen verwendet.

In der Astronomie sind die eulerschen Winkel unter anderen Bezeichnungen als Bahnelement eines Objekts geläufig.

In der Computergrafik werden die eulerschen Winkel zur Beschreibung der Orientierung eines Objektes verwendet.

In der Festkörper-NMR werden die eulerschen Winkel zur theoretischen Beschreibung und zur Simulation von Spektren benutzt.

Literatur

• Georg Rill, Thomas Schaeffer: Grundlagen und Methodik der Mehrkörpersimulation. Vieweg + Teubner, Wiesbaden 2010, ISBN 978-3-658-16009-8.

Weblinks

Commons: Euler angles – Album mit Bildern, Videos und Audiodateien

Wikibooks: Die Mechanik starrer Körper, Die eulerschen Winkel – Lern- und Lehrmaterialien

• Eric Weisstein: Euler Angles. In: MathWorld (englisch).