Ortsvektor

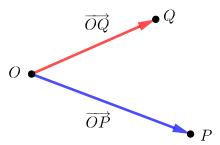
Als Ortsvektor (oder Radiusvektor) eines Punktes bezeichnet man in der Mathematik und in der Physik einen Vektor, der von einem festen Bezugspunkt zu diesem Punkt (Ort) zeigt. In der elementaren und der synthetischen Geometrie können diese Vektoren als Klassen von verschiebungsgleichen Pfeilen oder gleichwertig als Parallelverschiebungen definiert werden.

Ortsvektoren ermöglichen es, für die Beschreibung von Punkten, von Punktmengen und von Abbildungen die Vektorrechnung zu benutzen. Legt man ein kartesisches Koordinatensystem zu Grunde, dann wählt man in der Regel den Koordinatenursprung als Bezugspunkt für die Ortsvektoren der Punkte. In diesem Fall stimmen die Koordinaten eines Punktes bezüglich dieses Koordinatensystems mit den Koordinaten seines Ortsvektors überein.

In der analytischen Geometrie werden Ortsvektoren verwendet um Abbildungen eines affinen oder euklidischen Raums zu beschreiben und um Punktmengen (wie zum Beispiel Geraden und Ebenen) durch Gleichungen und Parameterdarstellungen zu beschreiben.

In der Physik werden Ortsvektoren verwendet um die Bewegung eines (oft als punktförmig) gedachten Körpers zu beschreiben.

Schreibweisen

In der Geometrie wird der Bezugspunkt (Ursprung) in der Regel mit $O$ (für lat. origo) bezeichnet. Die Schreibweise für den Ortsvektor eines Punktes $P$ ist dann

$\overrightarrow{OP}$ .

Gelegentlich werden auch die Kleinbuchstaben mit Vektorpfeil benutzt, die den Großbuchstaben entsprechen, mit denen die Punkte bezeichnet werden, zum Beispiel

$\vec p = \overrightarrow{OP},\ \vec q = \overrightarrow{OQ},\ \vec{a} = \overrightarrow{OA},\ \vec{b} = \overrightarrow{OB},\ \dots,\ \vec x = \overrightarrow{OX}$ .

In der Physik wird der Ortsvektor Radiusvektor  genannt und als $\vec r$ oder $\mathbf r$ geschrieben.

Beispiele und Anwendungen in der Geometrie

Verbindungsvektor

Für den Verbindungsvektor $\overrightarrow{PQ}$ zweier Punkte $P$ und $Q$ mit den Ortsvektoren $\vec p = \overrightarrow{OP}$ und $\vec q = \overrightarrow{OQ}$ gilt

$\overrightarrow{PQ} = \overrightarrow{OQ} - \overrightarrow{OP} = \vec q - \vec p$

Kartesische Koordinaten

Der Ortsvektor $\overrightarrow{OP}$ des Punkts $P(p_1| p_2| p_3)$ hat die Koordinaten

$\overrightarrow{OP} = \begin{pmatrix} p_1 \\ p_2 \\ p_3 \end{pmatrix}$

Verschiebung

Eine Verschiebung um den Vektor $\vec v$ bildet den Punkt $X$ auf den Punkt $X^\prime$ ab. Dann gilt für die Ortsvektoren:

$\overrightarrow{OX'} = \overrightarrow{OX} + \vec v$

$\vec x\,' = \vec x + \vec v$

Drehung um den Ursprung

Eine Drehung in der Ebene mit Drehzentrum O um den Winkel $\phi$ gegen den Uhrzeigersinn kann in kartesischen Koordinaten wie folgt mit Hilfe einer Drehmatrix beschrieben werden: Ist $\vec x = \tbinom{x_1}{ x_2} = \overrightarrow{OX}$ der Ortsvektor eines Punktes $X$ und $\vec x\,' = \tbinom{ x_1{}'}{ x_2{}'} = \overrightarrow{OX'}$ der Ortsvektor des Bildpunkts $\,X '$, so gilt:

$\begin{pmatrix} x_1{}' \\ x_2{}' \end{pmatrix} = \begin{pmatrix} \cos \varphi & -\sin \varphi \\ \sin \varphi & \cos\varphi \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}$

Affine Abbildung

Eine allgemeine affine Abbildung, die den Punkt $X$ auf den Punkt $X'$ abbildet, kann mit Ortsvektoren wie folgt dargestellt werden:

$\vec x' = L(\vec x) + \vec v$.

Hierbei ist $\vec x$ der Ortsvektor von $X$, $\vec x'$ der Ortsvektor von $X'$, $L$ eine lineare Abbildung und $\vec v$ ein Vektor, der eine Verschiebung beschreibt. In kartesischen Koordinaten kann die lineare Abbildung $L$ durch eine Matrix $A$ dargestellt werden und es gilt:

$\vec x = A \cdot \vec x + \vec v$.

Im dreidimensionalen Raum ergibt dies:

$\begin{pmatrix} x_1' \\ x_2' \\x_3' \end{pmatrix} = \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix} \, \begin{pmatrix} x_1 \\ x_2 \\x_3 \end{pmatrix} + \begin{pmatrix} v_1 \\ v_2 \\v_3 \end{pmatrix}$.

Entsprechende Darstellung gelten in andern Dimensionen.

Parameterdarstellung einer Geraden

Die Gerade durch die Punkte $P$ und $Q$ enthält genau die Punkte $X$, deren Ortsvektor $\vec x$ eine Darstellung

$\vec x = \overrightarrow{OP} + t \,\overrightarrow{PQ}$ mit $t \in \R$

besitzt.

Normalenform der Ebenengleichung

Die Ebene durch den Punkt $P$ (Stützpunkt) mit Normalenvektor $\vec n$ enthält genau die Punkte $X$, deren Ortsvektor $\vec x$ die Gleichung

$\vec x \cdot \vec n = \vec p \cdot \vec n$

erfüllt. Dabei ist $\vec p$ der Ortsvektor des Stützpunkts $P$ (Stützvektor), der Malpunkt bezeichnet das Skalarprodukt.

Ortsvektor in verschiedenen Koordinatensystemen

Kartesisches Koordinatensystem

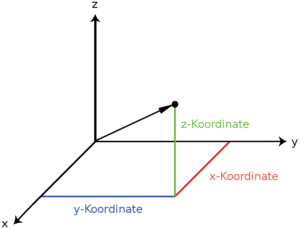
Der durch einen Ortsvektor beschriebene Punkt kann durch die Koordinaten eines Koordinatensystems ausgedrückt werden, wobei der Bezugspunkt des Ortsvektors normalerweise in den Koordinatenursprung gelegt wird.

Kartesische Koordinaten

Üblicherweise wird der Ortsvektor in kartesischen Koordinaten in der Form

$\vec r = \vec r\,(x,y,z) = \begin{pmatrix} x \\ y \\ z\end{pmatrix}$

definiert. Daher sind die kartesischen Koordinaten gleichzeitig die Komponenten des Ortsvektors.

Zylinderkoordinaten

Der Ortsvektor als Funktion von Zylinderkoordinaten ergibt sich durch Umrechnen der Zylinderkoordinaten in die entsprechenden kartesischen Koordinaten zu

$\vec r = \vec r\,(R,\varphi,z) = \begin{pmatrix} R\,\cos\varphi \\ R\,\sin\varphi \\ z\end{pmatrix}.$

Hier bezeichnet $R$ den Abstand des Punktes von der $z$-Achse, der Winkel $\phi$ wird von der $x$-Achse in Richtung der $y$-Achse gezählt. $R$ und $\phi$ sind als die Polarkoordinaten des orthogonal auf die $x$-$y$-Ebene projizierten Punkts.

Kugelkoordinaten

Der Ortsvektor als Funktion von Kugelkoordinaten ergibt sich durch Umrechnen der Kugelkoordinaten in die entsprechenden kartesischen Koordinaten zu

$\vec r = \vec r\,(r,\vartheta,\varphi) = \begin{pmatrix} r\,\sin\vartheta\,\cos\varphi \\ r\,\sin\vartheta\,\sin\varphi \\ r\,\cos\vartheta\end{pmatrix}.$

Hierbei bezeichnet $r$ den Abstand des Punkts vom Ursprung (also die Länge des Ortsvektors), der Winkel $\phi$ wird in der $x$-$y$-Ebene von der $x$-Achse aus in Richtung der $y$-Achse gemessen, der Winkel $\theta$ ist der Winkel zwischen der $z$-Achse und dem Ortsvektor.

Basisvektoren

Die Basisvektoren in den verschiedenen Koordinatensystemen ergeben sich durch Normierung der partiellen Ableitungen des Ortsvektors nach den jeweiligen Koordinaten. Allgemein ergibt sich der zur Koordinate k gehörende Basisvektor zu

$\vec e_k = \frac{\frac{\partial \vec r}{\partial k}}{\left|\frac{\partial \vec r}{\partial k}\right|}\,.$

Kartesische Koordinaten

$\vec e_x = \frac{\frac{\partial \vec r}{\partial x}}{\left|\frac{\partial \vec r}{\partial x}\right|} = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix},\quad \vec e_y = \frac{\frac{\partial \vec r}{\partial y}}{\left|\frac{\partial \vec r}{\partial y}\right|} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix},\quad \vec e_z = \frac{\frac{\partial \vec r}{\partial z}}{\left|\frac{\partial \vec r}{\partial z}\right|} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}.$

Die Basisvektoren $\vec e_x$, $\vec e_y$ und $\vec e_z$ sind zueinander orthonormal und bilden in dieser Reihenfolge ein Rechtssystem.

Zylinderkoordinaten

$\vec e_R = \frac{\frac{\partial \vec r}{\partial R}}{\left|\frac{\partial \vec r}{\partial R}\right|} = \begin{pmatrix} \cos\varphi \\ \sin\varphi \\ 0 \end{pmatrix},\quad \vec e_\varphi = \frac{\frac{\partial \vec r}{\partial \varphi}}{\left|\frac{\partial \vec r}{\partial \varphi}\right|} = \begin{pmatrix} -\sin\varphi \\ \cos\varphi \\ 0 \end{pmatrix},\quad \vec e_z = \frac{\frac{\partial \vec r}{\partial z}}{\left|\frac{\partial \vec r}{\partial z}\right|} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}.$

Die Basisvektoren $\vec e_R$, $\vec e_\varphi$ und $\vec e_z$ sind zueinander orthonormal und bilden in dieser Reihenfolge ein Rechtssystem.

Kugelkoordinaten

$\vec e_r = \frac{\frac{\partial \vec r}{\partial r}}{\left|\frac{\partial \vec r}{\partial r}\right|} = \begin{pmatrix} \sin\vartheta\,\cos\varphi \\ \sin\vartheta\,\sin\varphi \\ \cos\vartheta \end{pmatrix},\quad \vec e_\vartheta = \frac{\frac{\partial \vec r}{\partial \vartheta}}{\left|\frac{\partial \vec r}{\partial \vartheta}\right|} = \begin{pmatrix} \cos\vartheta\,\cos\varphi \\ \cos\vartheta\,\sin\varphi \\ -\sin\vartheta \end{pmatrix},\quad \vec e_\varphi = \frac{\frac{\partial \vec r}{\partial \varphi}}{\left|\frac{\partial \vec r}{\partial \varphi}\right|} = \begin{pmatrix} -\sin\varphi \\ \cos\varphi \\ 0\end{pmatrix}.$

Die Basisvektoren $\vec e_r$, $\vec e_\vartheta$ und $\vec e_\varphi$ sind zueinander orthonormal und bilden in dieser Reihenfolge ein Rechtssystem.

Wegelement

Ein Wegelement oder Linienelement $\mathrm{d} \vec s$ kann als totales Differential $\mathrm{d} \vec r$ des Ortsvektors dargestellt werden. Allgemein ergibt sich für das vektorielle Wegelement bei Verwendung der Koordinaten $k_i\,$:

$\mathrm{d}\vec s = \mathrm{d}\vec r = \sum_i \frac{\partial \vec r}{\partial k_i} \,\mathrm{d}k_i\,.$

Mit der obenstehenden Gleichung für die Basisvektoren kann man auch schreiben

$\mathrm{d}\vec s = \mathrm{d}\vec r = \sum_i \vec e_{k_i} \left| \frac{\partial \vec r}{\partial k_i} \right| \,\mathrm{d}k_i\,.$

Die Beträge der Ableitungen des Ortsvektors $\vec r$ nach den Koordinaten $k_i\,$ heißen metrische Koeffizienten

$g_{k_i} = \left| \frac{\partial \vec r}{\partial k_i} \right|.$

Damit kann man das vektorielle Wegelement in der Form

$\mathrm{d}\vec s = \mathrm{d}\vec r = \sum_i \vec e_{k_i}\,g_{k_i}\,\mathrm{d}k_i$

darstellen. Für die bisher betrachteten Koordinatensysteme ergeben sich daraus die folgenden Darstellungsformen:

• Kartesische Koordinaten:

$\mathrm{d}\vec s = \mathrm{d}\vec r = \vec e_x\,\mathrm{d}x + \vec e_y\,\mathrm{d}y + \vec e_z\,\mathrm{d}z \,,$

• Zylinderkoordinaten:

$\mathrm{d}\vec s = \mathrm{d}\vec r = \vec e_R\,\mathrm{d}R + \vec e_\varphi\,R\,\mathrm{d}\varphi + \vec e_z\,\mathrm{d}z \,,$

• Kugelkoordinaten:

$\mathrm{d}\vec s = \mathrm{d}\vec r = \vec e_r\,\mathrm{d}r + \vec e_\vartheta\,r\,\mathrm{d}\vartheta + \vec e_\varphi\,r\,\sin\vartheta\,\mathrm{d}\varphi \,.$

Relativistische Koordinaten

In der speziellen Relativitätstheorie (SRT) werden Raum und Zeit als eine zusammenhängende, vierdimensionale pseudoriemannsche Mannigfaltigkeit, der sogenannten Raumzeit, beschrieben. Ein Punkt auf dieser Mannigfaltigkeit, der durch 3 Raumkoordinaten und eine Zeitkoordinate festgelegt wird, wird als Ereignis bezeichnet. Für jeweils zwei Ereignisse kann durch die Minkowski-Metrik ein Linienelement ds definiert werden, welches zur Eigenzeit proportional ist.

$\mathrm ds^2=\eta_{\mu\nu}\mathrm dx^\mu \mathrm dx^\nu = c^2 \mathrm dt^2 - \mathrm dx^2 - \mathrm dy^2 - \mathrm dz^2$.

Hierbei bezeichnet $\eta_{\mu\nu}=diag(1,-1,-1,-1)$ die Minkowski-Metrik und $dx^\mu$ das Vierervektordifferential.

Physik

Trajektorie

In der Physik wird die Bewegung eines Punktes (zum Beispiel eines Massenpunkts oder des Schwerpunkts eines Körpers) durch eine Funktion beschrieben, die jedem Zeitpunkt $t$ den Ortsvektor $\vec r(t)$ des Massenpunkts zum Zeitpunkt $t$ zuordnet. Die so beschriebene Kurve heißt auch Trajektorie oder Bahnkurve.

Die Ableitung dieser vektorwertigen Funktion $\vec r(t)$ nach der Zeit t ergibt den Geschwindigkeitsvektor

$\vec v(t) = \dot {\vec r}(t) = \frac{\mathrm d}{\mathrm dt} \vec r(t)$.

Durch nochmalige Ableitung ergibt sich der Beschleunigungsvektor

$\vec a(t) = \dot {\vec v}(t) = \ddot {\vec r}(t) = \frac{\mathrm d^2}{\mathrm dt^2} \vec r(t)$.

Für die Länge des zwischen den Zeitpunkten $t_1$ und $t_2$ zurückgelegten Weges gilt

$s_{1,2} = \int_{t_1}^{t_2} \left|\dot{\vec r}(t)\right|\,\mathrm{d}t = \int_{t_1}^{t_2} \left|\vec v(t)\right|\,\mathrm{d}t \,.$

Himmelsmechanik

Um die Position eines Himmelskörpers, der sich auf einer Umlaufbahn um ein Schwerezentrum bewegt, anzugeben, wird in der Himmelsmechanik als Ursprung des Ort- oder Radiusvektors dieses Schwerezentrum gewählt. Der Radiusvektor liegt dann stets in Richtung der Gravitationslinie. Die Strecke des Ortsvektors wird Fahrstrahl genannt. Der Fahrstrahl spielt eine zentrale Rolle beim zweiten keplerschen Gesetz (Flächensatz).

Siehe auch

• Einheitsvektor
• Stützvektor
• Frenetsche Formeln
• Hodograph

Literatur

• Alexander Heigl: Mathematische Einführung in die Elektrizitätslehre (PDF, 634 kB). Lehrstuhl für Technische Elektrophysik, Technische Universität München. 18. Oktober 2006.
• Klaus Desch: Mathematische Ergaenzungen zur Physik II, Kapitel 11: Vektoranalysis (PDF, 210 kB). Institut für Experimentalphysik, Hamburg.