Heyting-Algebra
In der Mathematik sind Heyting-Algebren spezielle partielle Ordnungen; gleichzeitig ist der Begriff der Heyting-Algebra eine Verallgemeinerung des Begriffs der Booleschen Algebra. Heyting-Algebren entstehen als Modelle intuitionistischer Logik, einer Logik, in der der Satz vom ausgeschlossenen Dritten im Allgemeinen nicht gilt. Vollständige Heyting-Algebren sind ein zentraler Gegenstand der punktfreien Topologie.
Die Heyting-Algebra ist nach Arend Heyting benannt.
Formale Definition[Bearbeiten | Quelltext bearbeiten]
Eine Heyting-Algebra ist ein beschränkter Verband mit der Eigenschaft, dass es für alle und in ein größtes Element in gibt mit
Dieses Element wird das relative Pseudokomplement von bezüglich genannt und geschrieben.
Eine äquivalente Definition kann mittels folgender Abbildungen gegeben werden:
definiert als
für festes in . Ein beschränkter Verband ist eine Heyting-Algebra genau dann, wenn alle Abbildungen Linksadjungierte einer Galoisverbindung sind. In diesem Fall ist der jeweilige Rechtsadjungierte gegeben durch , wobei wie oben definiert wird.
Eine vollständige Heyting-Algebra ist eine Heyting-Algebra, die ein vollständiger Verband ist.
In jeder Heyting-Algebra kann man das Pseudokomplement eines Elements definieren durch , wobei 0 das kleinste Element der Heyting-Algebra ist. Es gilt , und zudem ist das größte Element mit dieser Eigenschaft. Jedoch gilt im Allgemeinen nicht , so dass nur ein Pseudokomplement und kein echtes Komplement ist.
Beispiele[Bearbeiten | Quelltext bearbeiten]
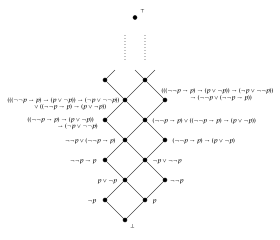
- Jede totale Ordnung, die ein beschränkter Verband ist, ist auch eine Heyting-Algebra mit
- Jede Boolesche Algebra ist eine Heyting-Algebra, mit definiert als .
- Jeder vollständige Verband , in dem für alle gilt ist bereits eine vollständige Heyting-Algebra mit . Endliche, beschränkte, distributive Verbände gehören in diese Klasse.
- Die einfachste Heyting-Algebra, die nicht schon eine Boolesche Algebra ist, ist die linear geordnete Menge { 0, ½, 1 } mit folgenden Operationen:
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
- Man sieht, dass den Satz vom ausgeschlossenen Dritten verletzt.
- Der Verband der offenen Mengen eines topologischen Raums ist eine vollständige Heyting-Algebra. In diesem Fall ist das Innere der Vereinigung von und , wobei das Komplement der offenen Menge bezeichnet. Nicht alle vollständigen Heyting-Algebren sind auf diese Weise erzeugbar. Damit zusammenhängende Fragen werden in der punktfreien Topologie untersucht, in der vollständige Heyting-Algebren auch Frames oder Locales genannt werden.
- Die Lindenbaum-Algebra der intuitionistischen Aussagenlogik ist eine Heyting-Algebra. Sie ist definiert als die Menge aller aussagenlogischen Formeln, geordnet durch die logische Folgerungsrelation: für zwei Formeln und sei genau dann, wenn . Dabei ist allerdings nur eine Quasiordnung, die eine partielle Ordnung induziert, welche dann die gewünschte Heyting-Algebra ist.
- Die globalen Elemente des Unterobjekt-Klassifikators eines Elementartopos bilden eine Heyting-Algebra; es ist die Heyting-Algebra der Wahrheitswerte der von dem Topos induzierten intuitionistischen Logik höherer Stufe.
- Die Heytingalgebra mit dem Hassediagramm ist ein minimales Beispiel mit Elementen , für die gilt, aber nicht (nämlich: L und R), wie auch ein minimales Beispiel mit Elementen , für die nicht gilt (nämlich:).
1 | M / \ L R \ / 0
Eigenschaften[Bearbeiten | Quelltext bearbeiten]
Heyting-Algebren sind stets distributiv, d. h.
- und
- .
Die Distributivität wird manchmal als Axiom postuliert, aber sie folgt schon aus der Existenz relativer Pseudokomplemente. Der Grund für das Gelten von 1) ist, dass als unterer Adjungierter einer Galois-Verbindung alle existierenden Suprema bewahrt. 1) ist aber nichts anderes als die Bewahrung binärer Suprema durch .
Mit einem ähnlichen Argument lässt sich folgendes infinitäres Distributivgesetz in vollständigen Heyting-Algebren zeigen:
für alle aus und Teilmengen von .
Ein Verband mit einer binären Operation ist eine Heyting-Algebra genau dann, wenn:
- ,
- ,
- ,
- .
Nicht jede Heyting-Algebra erfüllt die beiden De Morganschen Gesetze. Allerdings sind folgende Aussagen über eine beliebige Heyting-Algebra äquivalent:
- erfüllt beide De Morganschen Gesetze.
- , für alle .
- , für alle .
- , für alle .
Das Pseudokomplement eines Elements aus ist das Supremum der Menge , und es gehört zu dieser Menge (d. h. es gilt ).
Ein Element einer Heyting-Algebra heißt regulär, wenn eine der folgenden äquivalenten Bedingungen gilt:
- .
- für ein aus .
Eine Heyting-Algebra ist eine Boolesche Algebra genau dann, wenn eine der folgenden äquivalenten Bedingungen gilt:
In diesem Fall ist das Element gleich .
In jeder Heyting-Algebra sind das kleinste und das größte Element, 0 und 1, regulär.
Die regulären Elemente einer Heyting-Algebra bilden eine Boolesche Algebra. Wenn nicht alle Elemente der Heyting-Algebra regulär sind, ist diese Boolesche Algebra kein Unterverband der Heyting-Algebra, weil die Supremums-Operationen verschieden sind.
Ist eine Heyting-Algebra, so kann es sein, dass der dazu duale Verband ebenfalls eine Heyting-Algebra ist. Falls das so ist, kann man zu einem Element in das Pseudokomplement bilden und dieses als Element von auffassen. Es gilt dann immer . In der anderen Richtung gilt die Ungleichung im Allgemeinen nicht: ist äquivalent zu und zu .
Im Unterschied zu manchen mehrwertigen Logiken teilen Heyting-Algebren mit Booleschen Algebren die folgende Eigenschaft: Wenn die Negation einen Fixpunkt hat (also für ein ), dann ist die Heyting-Algebra trivial: sie besteht nur aus einem Element.
Bedeutung für intuitionistische Logik[Bearbeiten | Quelltext bearbeiten]
Arend Heytings Motivation, diesen Begriff einzuführen, war die Klärung der Bedeutung von intuitionistischer Logik für die Grundlagen der Mathematik. Das Peircesche Gesetz illustriert die Rolle, die Heyting-Algebren für die Semantik intuitionistischer Logik spielen. Das Peircesche Gesetz ist in klassischer Logik gültig, nicht aber in intuitionistischer Logik.
Eine Heyting-Algebra ist vom logischen Standpunkt aus gesehen eine Verallgemeinerung der üblichen Menge von Wahrheitswerten. Unter anderen entspricht dem größten Element 1 einer Heyting-Algebra der Wahrheitswert wahr; das kleinste Element 0 entspricht falsch. Die übliche zweiwertige Logik ist das einfachste Beispiel einer Heyting-Algebra – sie besteht nur aus diesen beiden Elementen. Abstrakt gesagt ist die zwei-elementige Boolesche Algebra auch (wie jede Boolesche Algebra) eine Heyting-Algebra.
Klassisch gültige Formeln sind solche, die unter jeden möglichen Belegung der aussagenlogischen Variablen in der zweiwertigen Booleschen Algebra den Wert 1 (wahr) ergeben, d. h. die üblichen aussagenlogischen Tautologien. (Äquivalent dazu können auch alle Belegungen in allen Booleschen Algebren betrachtet werden.) Intuitionistisch gültige Formeln sind hingegen solche, die für alle Heyting-Algebren und alle Belegungen den Wert 1 ergeben. In der oben angegebenen dreielementigen Heyting-Algebra ist der Wert von Peirces Gesetz nicht immer 1: wenn man mit ½ und mit 0 belegt, dann ist der Wert nicht 1, sondern nur ½. Nach oben Gesagtem bedeutet das, dass das Peircesche Gesetz intuitionistisch nicht gültig ist – klassisch ist es aber schon gültig.
Literatur[Bearbeiten | Quelltext bearbeiten]
- Marcello Bonsangue, Bart Jacobs, Joost N. Kok: Duality Beyond Sober Spaces. Topological Spaces and Observation Frames (= Faculteit der Wiskunde en Informatica. Informatica Rapport. IR-350, ZDB-ID 777097-2). Vrije Universiteit – Faculteit der Wiskunde en Informatica, Amsterdam 1994.
- Francis Borceux: Handbook of Categorical Algebra. Band 3: Categories of Sheaves (= Encyclopedia of Mathematics and its Applications. 52). Cambridge University Press, Cambridge u. a. 1994, ISBN 0-521-44180-3.
- Gerhard Gierz, Karl H. Hofmann, Klaus Keimel, Jimmie D. Lawson, Michael W. Mislove, Dana S. Scott: Continuous Lattices and Domains (= Encyclopedia of Mathematics and its Applications. 93). Cambridge University Press, Cambridge u. a. 2003, ISBN 0-521-80338-1.
- Peter T. Johnstone: Stone Spaces. (= Cambridge Studies in Advanced Mathematics. 3). Cambridge University Press, Cambridge u. a. 1986, ISBN 0-521-33779-8.
- Daniel E. Rutherford: Introduction to Lattice Theory. Oliver and Boyd, Edinburgh u. a. 1965.










































































