Morphismus (Varietät)
Ein Morphismus von Varietäten ist in der algebraischen Geometrie eine Abbildung von Varietäten mit bestimmten Regularitätseigenschaften. Ein Morphismus affiner Varietäten ist eine polynomiale Abbildung. Morphismen affiner Varietäten entsprechen eindeutig Homomorphismen ihrer Koordinatenringe. Die Definition kann auf quasiaffine, projektive und quasiprojektive Varietäten verallgemeinert werden, indem man Morphismen mit Hilfe regulärer Funktionen lokal definiert.
Morphismen abstrakter Varietäten sind lokale Garbenmorphismen.
(Bemerkung: Die Bezeichnung ist in der Literatur nicht einheitlich. Zum Teil wird auch für einen Morphismus der Ausdruck reguläre Abbildung verwendet, nicht zu verwechseln mit regulären Funktionen.)[1]
Definitionen[Bearbeiten | Quelltext bearbeiten]
Affine Varietäten[Bearbeiten | Quelltext bearbeiten]
bezeichne den n-dimensionalen affinen Raum über einem Körper k.
Eine Teilmenge ist eine algebraische Menge, wenn sie durch ein Ideal bestimmt wird:
Eine algebraische Menge ist eine affine Varietät, wenn sie sich nicht als echte Vereinigung zweier algebraischer Mengen schreiben lässt.
Sind und algebraische Mengen bzw. affine Varietäten, so heißt eine Abbildung
Morphismus, wenn es Polynome gibt, sodass für die Abbildung
gilt, dass
Ein Isomorphismus ist ein bijektiver Morphismus, dessen Umkehrabbildung ebenfalls ein Morphismus ist. Es gibt bijektive Morphismen, die keine Isomorphismen sind.
Die Morphismen von nach bilden eine -Algebra, den Koordinatenring, der mit bezeichnet wird. Es gibt einen kanonischen Isomorphismus
wobei das Verschwindungsideal von ist:
Zusammenhang mit Algebrenhomomorphismen[Bearbeiten | Quelltext bearbeiten]
Ist ein Morphismus
dann ist
definiert durch
ein Homomorphismus von -Algebren.
Diese Zuordnung ist ein kontravarianter Funktor von der Kategorie der algebraischen Mengen in die Kategorie der reduzierten -Algebren von endlichen Typ. Jede reduzierte -Algebra ist isomorph zu einem . Der Funktor ist eine Äquivalenz von Kategorien.
Die Zuordnung ist auch ein kontravarianter Funktor von der Kategorie der affinen Varietäten in die Kategorie der nullteilerfreien -Algebren von endlichen Typ. Auch dies ist eine Äquivalenz von Kategorien.
Affine, quasiaffine, projektive und quasiprojektive Varietäten[Bearbeiten | Quelltext bearbeiten]
Um die Definition auf quasiaffine, projektive und quasiprojektive Varietäten zu erweitern, werden zunächst reguläre Funktionen definiert, um dann einen Morphismus lokal zu definieren.
Reguläre Funktionen[Bearbeiten | Quelltext bearbeiten]
Ist eine quasiaffine Varietät, so ist eine Funktion regulär in einem Punkt , wenn es eine offene Umgebung mit gibt und Polynome gibt, sodass nirgendwo auf Nullstellen hat und
Ist eine quasiprojektive Varietät, so ist eine Funktion regulär in einem Punkt , wenn es eine offene Umgebung mit gibt und homogene Polynome mit demselben Grad gibt, sodass nirgendwo auf Nullstellen hat und
und sind keine Funktionen auf dem , aber ist eine wohldefinierte Funktion, da und homogen vom gleichen Grad sind.
Ist eine quasiaffine oder eine quasiprojektive Varietät, so ist eine Funktion regulär, wenn sie auf jedem Punkt in regulär ist.
Wird der Körper mit dem affinen Raum identifiziert, so ist eine reguläre Funktion stetig in der Zariski-Topologie. (Umgekehrt ist aber nicht jede stetige Abbildung eine reguläre Funktion.)
Morphismen[Bearbeiten | Quelltext bearbeiten]
Im Folgenden sind und affine, quasiaffine, projektive oder quasiprojektive Varietäten.
Diese Objekte tragen auf natürliche Weise eine Topologie, nämlich die Zariski-Topologie, in der die abgeschlossenen Mengen genau die algebraischen Mengen sind.
Ein Morphismus von nach ist eine stetige Funktion , die reguläre Funktionen von auf reguläre Funktionen von zurückholt. Genauer:
- Eine stetige Funktion ist ein Morphismus, wenn für alle offenen Teilmengen gilt, dass, falls eine reguläre Funktion ist, dann auch regulär auf ist.
Rationale Abbildung[Bearbeiten | Quelltext bearbeiten]
Eine rationale Abbildung ist ein Morphismus von einer offenen Menge nach , sodass keine Fortsetzung auf einer echten Obermenge von hat. Ist , so wird regulär in genannt. Ein Morphismus wird daher auch reguläre Abbildung genannt.
Beispiele[Bearbeiten | Quelltext bearbeiten]
Neilsche Parabel[Bearbeiten | Quelltext bearbeiten]
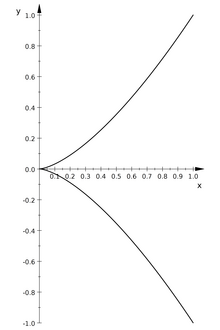
Ein Isomorphismus ist bijektiv und ein Homöomorphismus, aber ein bijektiver Homöomorphismus ist nicht unbedingt ein Isomorphismus: Ist die Neilsche Parabel,
so ist die Abbildung
ein bijektiver Homöomorphismus, der kein Isomorphismus ist, da die Umkehrabbildung kein Morphismus ist.
Quasiaffine Varietäten[Bearbeiten | Quelltext bearbeiten]
Es ist nicht immer möglich, Morphismen von quasiaffinen Varietäten durch Einschränkungen ihrer affinen Obervarietät zu definieren, da nicht jeder Morphismus einer quasiaffinen Varietät eine Einschränkung eines Morphismus der Obervarietät ist. Die Varietät ist quasiaffin. Der Morphismus:
ist ein Isomorphismus, für den es keinen Morphismus gibt mit
Es gilt
- und
Für den Morphismus mit , also und gilt hingegen .
Es lässt sich ein Isomorphismus von zu einer affinen Varietät angeben. Ist nämlich allgemein ein irreduzibles Polynom und
die entsprechende quasiaffine Varietät, außerdem die Hyperfläche
so ist die Abbildung
ein Isomorphismus.
Entfernt mal aber aus einer affinen Varietät eine Untervarietät der Kodimension größer als 1, so ist diese Varietät nicht affin.
Bilder von Morphismen[Bearbeiten | Quelltext bearbeiten]
Bilder quasiprojektiver Varietäten unter Morphismen sind im Allgemeinen keine quasiprojektiven Varietäten. Betrachtet man etwa den Morphismus
so erhält man als Bild . Dies ist keine lokalabgeschlossene Menge in . Das Bild ist jedoch stets eine konstruierbare Menge. Allgemein gilt, dass Morphismen konstruierbare Mengen auf konstruierbare Mengen abbilden.[2]
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Harris, Joe: Algebraic geometry. A first course. Corrected reprint of the 1992 original. Graduate Texts in Mathematics, 133. Springer-Verlag, New York, 1995. ISBN 0-387-97716-3
- ↑ Joe Harris: Algebraic Geometry. A First Course. Springer, New Your 1992, ISBN 3-540-97716-3, Theorem 3.16.
Literatur[Bearbeiten | Quelltext bearbeiten]
- Brüske, Ischebeck, Vogel: Kommutative Algebra, Bibliographisches Institut (1989), ISBN 978-3411140411
- Klaus Hulek: Elementare Algebraische Geometrie. Vieweg, Braunschweig/Wiesbaden 2000, ISBN 3-528-03156-5.
- Robin Hartshorne: Algebraic Geometry, Springer-Verlag, New York/Berlin/Heidelberg 1977, ISBN 3-540-90244-9


![{\displaystyle I\subset k[x_{1},\ldots ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/adadfaa2ece8cb5229e383d8170d88a24039cbb7)



![{\displaystyle f_{1},\ldots ,f_{m}\in k[x_{1},\ldots ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ea74fc730c5b75358788778ea6b5152695c4974)





![{\displaystyle k[V]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1741d36e6904bb3d9bb000011dfe16bfe78cc0a1)
![{\displaystyle k(x_{1},\ldots ,x_{n})/I(V)\to k[V]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bec8ab10c021772e7c3a27be283d9cc51ef44021)

![{\displaystyle I(V):=\{f\in k[x_{1},\ldots ,x_{n}]|f(x_{1},\ldots ,x_{n})=0{\text{ für alle }}(x_{1},\ldots ,x_{n})\in V\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/942c2a782def9795cdb5c07aa4bd80deed2a3806)



![{\displaystyle \alpha ^{*}\colon k[W]\to k[V]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc7b96d887cd822fbdbb3ad6e9b3e5b74b38a995)






![{\displaystyle g,h\in k[x_{1},\ldots ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db5e89e95909ab10eb059305c3a5368212a970f8)



![{\displaystyle g,h\in k[x_{0},x_{1},\ldots ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d30b842fb80b4ce3dc3a582465948ba2ca871d8)






























![{\displaystyle h\in k[x_{1},\ldots ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd01c8b493e947c1c4bc2941f2b576e3d7816915)







