Bandpass

Als Bandpass (auch Bandbreitenfilter) wird in der Elektrotechnik, Tontechnik und Optik ein Filter bezeichnet, das nur Signale eines Frequenzbands passieren lässt. Die Frequenzbereiche unterhalb und oberhalb des Durchlassbereiches werden dabei gesperrt oder deutlich abgeschwächt. Ein Bandpass stellt das Gegenstück zur Bandsperre dar.
Je nach Anwendungsbereich handelt es sich dabei um optische, akustische oder elektrische Bandpassfilter. Ein spezieller, schmalbandiger elektrischer Bandpass ist das Bandfilter, welches unter anderem zur Kanaltrennung in Überlagerungsempfängern eingesetzt wird.
Eigenschaften[Bearbeiten | Quelltext bearbeiten]
Ein Bandpass lässt sich auf folgende Arten erzeugen:
- Reihenschaltung eines Hochpasses mit einem Tiefpass mit deutlich unterschiedlichen Grenzfrequenzen ('uneigentlicher Bandpass'), wenn ein relativ breiter Durchlassbereich erwünscht ist. Die Flankensteilheit wird dann allein über die Charakteristik des Hoch- und Tiefpasses definiert. Ein Beispiel dafür ist der Lautsprecherweichen-Zweig für den Mitteltöner in einer Dreiwege-Lautsprecherbox.
- ein oder mehrere mehr oder weniger gedämpfte Schwingkreise mit Induktivität (Spule) und Kapazität (Kondensator). Dabei wirken Reihenschwingkreise in der Leitung (geringe Impedanz bei Resonanz) und Parallelschwingkreise zwischen Leitung und Bezug/Masse (hohe Impedanz bei Resonanz).
- zwei oder mehrere entweder elektrisch oder magnetisch gekoppelte Schwingkreise. Charakteristisch ist dabei eine leicht überkritische Kopplung, die zur Aufspaltung der Resonanzfrequenz in zwei nahe beieinanderliegende Maxima führt. Damit kann eine meist erwünschte, hutförmige Übertragungsfunktion gut angenähert werden. Beispiele sind die Bandfilter aller klassischen Zwischenfrequenzverstärker in Fernseh- und Rundfunkempfängern nach dem Superhet-Prinzip sowie auch Filter in Streifenleiter-Technik (z. B. Haarnadelfilter, siehe weiter unten).
- aktive Filter, etwa Sallen-Key-Filter, enthalten aktive Elemente (Verstärker) und eine Rückführung. Sie können ohne Spulen hohe Filtersteilheiten erreichen.
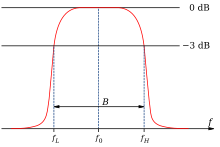
Der Durchlassbereich, welcher mit der Übertragungsfunktion dargestellt wird, ist durch die Bandbreite B um die Mittenfrequenz f0 charakterisiert. Die Mittenfrequenz ist definiert als das geometrische Mittel von fH und fL:
Die Bandbreite B des Filters ist die Differenz zwischen der oberen und der unteren Grenzfrequenz (fH und fL). Die Grenzfrequenzen sind durch eine Reduktion des Pegels um 3 dB gegenüber dem Maximalwert definiert.
Bandpässe weisen mindestens eine Filterordnung von zwei auf. Bandpässe mit symmetrischer Übertragungsfunktion um die Mittenfrequenz f0 weisen eine gerade Filterordnung auf.
Bandpass 2. Ordnung[Bearbeiten | Quelltext bearbeiten]


Der einfachste Bandpass mit Schwingkreis ist ein Bandpass 2. Ordnung, wie er als elektrisch passiver Filter in nebenstehender Abbildung skizziert ist. Bandpässe 2. Ordnung weisen abseits des Durchlassbereichs eine Flankensteilheit von 20 dB pro Dekade auf und die Übertragungsfunktion mit den Werten der Bauelemente R, L und C lautet:
Allgemein kann die Übertragungsfunktion auch durch einen Dämpfungsgrad D und der Resonanzkreisfrequenz ω0 ausgedrückt werden. Der Zusammenhang zu der Bandbreite B und Resonanzfrequenz f0 ist:
Alternativ kann die Übertragungsfunktion auch mit einem Gütefaktor Q:
ausgedrückt werden. Hohe Gütefaktoren Q ergeben schmalbandige Bandfilter.
Bandpässe höherer Ordnung[Bearbeiten | Quelltext bearbeiten]

Bandpassfilter höher Ordnung weisen zum Sperrbereich hin steilere Filterflanken auf und können im Gegensatz zu den Bandfiltern 2. Ordnung im Durchlassbereich einen flacheren Verlauf des Betragsfrequenzganges aufweisen. Die Übertragungsfunktion für einen Bandpass 4. Ordnung lautet beispielsweise:
mit den allgemeinen Koeffizienten a1, b1, b2 und b3.
Anwendungsbereiche[Bearbeiten | Quelltext bearbeiten]
Elektronik[Bearbeiten | Quelltext bearbeiten]


In der Elektronik werden bei Frequenzen unterhalb etwa 10 MHz kontinuierliche Bandpassfilter als aktive oder passive Filter angewendet. Elektrische Bandpassfilter können als eine rückwirkungsfreie Kombination von einem Hochpass und einem Tiefpass ausgedrückt werden wie in Terzfiltern und Oktavfiltern, die genormte Übertragungsfunktionen mit sehr steilen Flanken besitzen. Typische Bauelemente sind Kondensatoren, Widerstände und Spulen. Bei aktiven Bandpässen im Niederfrequenzbereich werden Filtereigenschaften durch zusätzliche Operationsverstärker verbessert. Die Dimensionierung kann sich an dem Filterentwurf von Tiefpassfiltern orientieren, wobei der Bandpass mit gerader Filterordnung durch eine Tiefpass-Bandpass-Transformation gebildet wird.
Falls das Signal vorher durch Analog-Digital-Umsetzer digitalisiert wurde, bieten die Verfahren der digitalen Signalverarbeitung sehr effektive und wirtschaftliche Methoden, da Bandpässe wie andere Filter auch als zeitdiskrete Filter realisiert werden können. Die quantisierten Filterkoeffizienten für das digitale Bandpassfilter können beispielsweise durch die bilineare Transformation aus dem zeitkontinuierlichen, analogen Filter gewonnen werden.
Im Bereich der Hochfrequenz um 100 MHz nutzt man dagegen die Erscheinung der Resonanz aus, denn Schwingkreise können – abhängig von ihrer Schaltung – hochohmig (Parallelschwingkreis) beziehungsweise niederohmig (Reihenschwingkreis) werden. Deren Eigenschaften werden von den kleineren Akustische-Oberflächenwellen-Filtern und Quarzfiltern erheblich übertroffen. Hauptanwendung ist die Frequenzselektion in Überlagerungsempfängern auf der Zwischenfrequenzebene. Bei aufwändig ausgelegten Empfängern wurden mehrere solcher Bandfilter jeweils mit einer Verstärkerstufe versehen und hintereinander geschaltet, um eine besonders hohe Trennschärfe zu erreichen.
Im Mikrowellenbereich bestehen Bandpässe oft aus Streifenleitern oder auch aus Löchern und Schlitzen in beziehungsweise zwischen Hohlleitern. Dielektrische Resonatoren sind klein und besitzen sehr hohe Gütefaktoren.
Lautsprecher[Bearbeiten | Quelltext bearbeiten]
Als Bandpasslautsprecher wird ein Lautsprechergehäuse bezeichnet, bei dem der Lautsprecher keine direkte Kopplung zum Schallraum aufweist. Er ist also von außen nicht zu sehen, der komplette Schall wird über die „Reflexöffnung(en)“ abgegeben. Im Inneren besteht das System meist aus zwei Kammern, von denen mindestens eine als Bassreflex-Gehäuse ausgeführt ist.
Durch diese Bauweise werden höhere Frequenzanteile (Mittel- und Hochtonbereich) ohne elektrische Frequenzweiche herausgefiltert. Solche Gehäuse dienen zur reinen Basswiedergabe.
Optik[Bearbeiten | Quelltext bearbeiten]
Bandpässe für optische Wellenlängen sind Farbfilter. Sie bestehen häufig aus Interferenzfiltern und können sehr schmalbandig ausgeführt werden. Ein weiterer verstellbarer, schmalbandiger optischer Bandpass ist der Monochromator.
Literatur[Bearbeiten | Quelltext bearbeiten]
- Ulrich Tietze, Christoph Schenk: Halbleiter-Schaltungstechnik. 12. Auflage. Springer, Berlin 2002, ISBN 3-540-42849-6.
- B. A. Shenoi: Introduction to Digital Signal Processing and Filter Design. Wiley-Interscience, Hoboken, NJ 2006, ISBN 0-471-46482-1.




