Bipartiter Graph

K_3,3: vollständig bipartiter Graph mit 3 Knoten pro Teilmenge

Ein einfacher, nicht vollständiger, bipartiter Graph mit Partitionsklassen $U$ und $V$

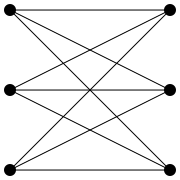
Ein bipartiter oder paarer Graph ist ein mathematisches Modell für Beziehungen zwischen den Elementen zweier Mengen. Es eignet sich sehr gut zur Untersuchung von Zuordnungsproblemen. Des Weiteren lassen sich für bipartite Graphen viele Grapheneigenschaften mit deutlich weniger Aufwand berechnen als dies im allgemeinen Fall möglich ist.

Definitionen

Ein einfacher Graph $G=(V,E)$ heißt bipartit oder paar, falls sich seine Knoten in zwei disjunkte Teilmengen A und B aufteilen lassen, sodass zwischen den Knoten innerhalb beider Teilmengen keine Kanten verlaufen. Das heißt, für jede Kante $\{v,w\}\in E$ gilt entweder $v\in A$ und $w\in B$ oder $v\in B$ und $w\in A$. Die Menge $\{A,B\}$ bezeichnet man dann als Bipartition des Graphen $G$ und die Mengen $A,B$ als Partitionsklassen. Vereinfacht dargestellt, ist ein bipartiter Graph ein Graph, in dem zwei Gruppen von Knoten existieren, innerhalb derer keine Knoten miteinander verbunden sind.

Der Graph $G$ heißt vollständig bipartit, falls eine Bipartition $\{A,B\}$ existiert, sodass jeder Knoten aus $A$ mit jedem Knoten aus $B$ verbunden ist. Einen solchen Graphen bezeichnet man auch als $K_{m,n}$, wobei $m$ und $n$ jeweils die Anzahl der Knoten von $A$ und $B$ sind. Ein vollständig bipartiter Graph, bei dem $m=1$ oder $n=1$ ist, heißt Sterngraph.

Eigenschaften

Für alle bipartiten Graphen gilt:

• Die Paarungszahl entspricht der Knotenüberdeckungszahl.
• Die Partitionsklassen $A,B$ sind schon nach Definition stabile Mengen.
• Der chromatische Index entspricht seinem Maximalgrad. Eine gültige Kantenfärbung lässt sich in $O(n\cdot m)$ bestimmen.
• Jeder bipartite Graph ist 2-knotenfärbbar. Jede Partitionsklasse bekommt also eine Farbe zugewiesen. Umgekehrt ist auch jeder 2-färbbare Graph bipartit.
• Ein ${\textstyle k}$-regulärer bipartiter Graph besitzt ${\textstyle k}$ disjunkte perfekte Matchings.
• Ein Graph ist genau dann bipartit, wenn er keinen Kreis ungerader Länge enthält.
• Die kantenchromatische Zahl entspricht seinem Maximalgrad.
• Der Listenchromatische Index ist gleich dem chromatischen Index. Damit sind bipartite Graphen eine Klasse von Graphen, für welche die Listenfärbungsvermutung zutrifft.
• Es gilt $\chi _{T}(G)\leq \Delta (G)+2$, wobei $\chi _{T}(G)$ die totalchromatische Zahl ist und $\Delta (G)$ der Maximalgrad. Für bipartite Graphen gilt also die Totalfärbungsvermutung.
• Alle bipartiten Graphen sind perfekte Graphen, somit stimmt für jeden induzierten Teilgraphen die Cliquenzahl mit der chromatischen Zahl überein.

Nach dem Satz von König entspricht in bipartiten Graphen die Größe der minimalen Knotenüberdeckung der Größe des maximalen Matchings. Eine alternative und äquivalente Form dieses Satzes besteht darin, dass die Größe der maximalen unabhängigen Menge plus die Größe des maximalen Matchings gleich der Anzahl der Knoten ist. In jedem Graphen ohne isolierte Knoten entspricht die Größe der minimalen Kantenüberdeckung plus der Größe eines maximalen Matchings der Anzahl der Knoten. Aus der Kombination dieser Gleichung mit dem Satz von König folgt, dass in bipartiten Graphen die Größe der minimalen Kantenüberdeckung gleich der Größe der maximalen unabhängigen Menge ist und dass die Größe der minimalen Kantenüberdeckung plus der Größe der minimalen Knotenüberdeckung gleich der Anzahl der Knoten ist.

Außerdem gilt: Jeder bipartite Graph, das Komplement jedes bipartiten Graphen, der Kantengraph jedes bipartiten Graphen und das Komplement des Kantengraphen jedes bipartiten Graphen sind alle perfekte Graphen. Dies war eines der Ergebnisse, die die Definition perfekter Graphen motivierten.

Nach dem Satz der starken perfekten Graphen haben die perfekten Graphen eine verbotene Charakterisierung, die der von bipartiten Graphen ähnelt: Ein Graph ist genau dann bipartit, wenn er keinen ungeraden Zyklus als Teilgraph hat, und ein Graph ist genau dann perfekt, wenn er keinen ungerader Zyklus oder sein Komplementgraphen als induzierten Teilgraphen hat. Die bipartiten Graphen, Kantengraphen von bipartiten Graphen und ihre Komplementgraphen bilden vier der fünf Grundklassen perfekter Graphen, die für den Beweis des Satzes der starken perfekten Graphen verwendet werden.

Für einen Knoten wird die Anzahl benachbarter Knoten als Grad des Knoten bezeichnet und als $\deg(v)$ bezeichnet. Die Gradsummenformel für einen bipartiten Graphen besagt, dass

$\sum _{v\in A}\deg(v)=\sum _{u\in B}\deg(u)=|E|$

Die Gradfolge eines bipartiten Graphen ist das Paar von Listen, das jeweils die Knotengrade der beiden Partitionsklassen $A$ und $B$ enthält. Beispielsweise hat der vollständige bipartiten Graph $K_{3,5}$ die Gradfolge $(5,5,5),(3,3,3,3,3)$. Isomorphe bipartite Graphen haben die gleiche Gradfolge. Die Gradfolge identifiziert jedoch im Allgemeinen einen bipartiten Graphen nicht eindeutig. In einigen Fällen können nicht-isomorphe zweigliedrige Graphen die gleiche Gradfolge aufweisen.

Kombinatorik

Die Anzahl der bipartiten Graphen steigt schneller als exponentiell mit der Anzahl $n$ der Knoten. Die folgende Tabelle zeigt die mit Hilfe eines Computers bestimmten Anzahlen für $n\leq 12$:

Anzahl der bipartiten Graphen
n	alle	zusammenhängend
1	1	1
2	2	1
3	3	1
4	7	3
5	13	5
6	35	17
7	88	44
8	303	182
9	1119	730
10	5479	4032
11	32303	25598
12	251135	212780

Algorithmen

Siehe auch: Graphpartitionierung

Mit dem Algorithmus von Hopcroft und Karp lässt sich in der Laufzeit $O(m{\sqrt {n}})$ ein maximales Matching finden und darüber auch die Stabilitätszahl bestimmen.

Mit einem einfachen Algorithmus, der auf Tiefensuche basiert, lässt sich in linearer Laufzeit bestimmen, ob ein Graph bipartit ist, und eine gültige Partition bzw. 2-Färbung ermitteln. Dabei wird einem beliebigen Knoten eine Farbe, und seinen Kindern die jeweils komplementäre Farbe zugewiesen. Wird beim Färben festgestellt, dass zwei benachbarte Knoten die gleiche Farbe haben, ist der Graph nicht bipartit.

Die Hauptidee besteht darin, jedem Knoten die Farbe zuzuweisen, die sich von der Farbe des übergeordneten Knotens in der Tiefensuche unterscheidet, und Farben in der Hauptreihenfolge der Tiefensuche zuzuweisen. Dies führt zwangsläufig zu einer 2-Färbung des aufspannenden Waldes, der aus den Kanten besteht, die die Knoten mit ihren übergeordneten Knoten verbinden, aber möglicherweise werden einige Kanten, die nicht zum Wald gehören, nicht richtig gefärbt. Einer der beiden Endknoten jeder Kante, die nicht zum Wald gehört, ist ein Vorfahr des anderen Endknotens. Wenn bei der Tiefensuche eine Kante dieses Typs entdeckt wird, sollte überprüft werden, ob diese beiden Knoten unterschiedliche Farben haben. Wenn dies nicht der Fall ist, bildet der Pfad im Wald vom Vorfahren zum Nachkommen zusammen mit der falsch gefärbten Kante einen ungeraden Zyklus, der vom Algorithmus zusammen mit dem Ergebnis zurückgegeben wird, dass der Graph nicht bipartit ist. Wenn der Algorithmus jedoch beendet wird, ohne einen ungeraden Zyklus dieses Typs zu finden, muss jede Kante richtig gefärbt sein, und der Algorithmus gibt die Färbung zusammen mit dem Ergebnis zurück, dass der Graph bipartit ist.

Alternativ kann ein ähnlicher Algorithmus mit Breitensuche anstelle der Tiefensuche verwendet werden. Wiederum erhält jeder Knoten die entgegengesetzte Farbe zu seinem übergeordneten Knoten im Suchbaum in der Reihenfolge der Breitensuche. Wenn beim Färben eines Knotens eine Kante vorhanden ist, die ihn mit einem zuvor gefärbten Knotens mit derselben Farbe verbindet, bildet diese Kante zusammen mit den Pfaden im Suchbaum der Breitensuche ihrer beiden Endpunkte mit ihrem letzten gemeinsamen Vorfahren einen ungeraden Zyklus. Wenn der Algorithmus beendet wird, ohne auf diese Weise einen ungeraden Zyklus zu finden, muss er eine korrekte Färbung gefunden haben und kann daraus schließen, dass der Graph bipartit ist.

Für die Schnittgraphen mit $n$ Strecken oder andere einfache Formen in der euklidischen Ebene ist es möglich, mit einer Laufzeit von ${\mathcal {O}}(n\cdot \log(n))$ zu testen, ob der Graph bipartit ist und entweder eine 2-Färbung oder einen ungeraden Zyklus zu finden, obwohl der Graph selbst bis zu ${\mathcal {O}}(n^{2})$ Kanten haben kann.

Matchings

→ Hauptartikel: Matching (Graphentheorie)

Ein Matching in einem Graphen ist eine Teilmenge seiner Kanten, von denen keine zwei einen Knoten gemeinsam haben. Algorithmen mit polynomieller Laufzeit sind für viele Anwendungen mit Matchings bekannt, einschließlich maximaler Matchings, dem Maximum Weight Matching und dem Stable Marriage Problem.

In vielen Fällen sind Matching-Probleme für bipartite Graphen einfacher zu lösen als für nicht bipartite Graphen, und viele Matching-Algorithmen wie der Algorithmus von Hopcroft und Karp für maximale Matchings funktionieren nur für bipartite Graphen korrekt.

Nehmen wir als einfaches Beispiel an, dass eine Gruppe $P$ von Personen Jobs aus einer Menge $J$ von Jobs sucht, wobei nicht alle Personen für alle Jobs geeignet sind. Diese Situation kann als bipartiter Graph $(P,J,E)$ modelliert werden, bei dem eine Kante jeden Arbeitssuchenden mit jedem geeigneten Job verbindet. Eine perfektes Matching beschreibt eine Möglichkeit, alle Arbeitssuchenden gleichzeitig zufrieden zu stellen und alle Jobs zu besetzen. Der Heiratssatz liefert eine Charakterisierung der bipartiten Graphen, die eine perfektes Matching ermöglichen. Das National Resident Matching Program in den Vereinigten Staaten verwendet Matching-Algorithmen, um dieses Problem für Medizinstudenten und Jobs in Krankenhäusern zu lösen.

Verallgemeinerung

Ein k-partiter Graph ist ein Graph, dessen Knotenmenge in $k$ Partitionen unterteilt werden kann, sodass es keine Kante zwischen zwei Knoten einer Partition gibt.

Programmierung

Das folgende Beispiel in der Programmiersprache C# zeigt die Implementierung eines Algorithmus, der prüft, ob ein ungerichteter Graph bipartit ist. Der ungerichtete Graph wird als zweidimensionales Array für die Adjazenzmatrix deklariert. Der Algorithmus weist benachbarten Knoten alternierende Farben zu. Bei der Ausführung des Programms wird die Methode Main verwendet, die das Ergebnis auf der Konsole ausgibt.

using System;
using System.Collections.Generic;

class BipartiteGraph
{
	// Diese Methode gibt true zurück, wenn der Graph bipartit ist, sonst false. Benachbarten Knoten werden alternierende Farben zugewiesen.
	private static bool IsBipartite(int[,] graph, int startIndex, int[] coloredVertices)
	{
		coloredVertices[startIndex] = 1; // Weist dem Startknoten eine Farbe zu
		Queue<int> queue = new Queue<int>(); // Deklariert eine Queue für die Knotenindexe
		queue.Enqueue(startIndex); // Fügt den Startknoten der Queue hinzu
		while (queue.Count != 0) // Solange die Queue nicht leer ist
		{
			int index = queue.Peek(); // Index des vordersten Knotens
			queue.Dequeue(); // Entfernt den vordersten Knoten
			if (graph[index, index] == 1) // Wenn der Graph eine Schleife enthält, wird false zurückgegeben
			{
				return false;
			}
			for (int i = 0; i < coloredVertices.Length; i++) // for-Schleife, die die Knoten durchläuft
			{
				if (graph[index, i] == 1 && coloredVertices[i] == -1) // Wenn die Knoten verbunden sind und der Zielknoten nicht gefärbt ist
				{
					coloredVertices[i] = 1 - coloredVertices[index]; // Weist dem benachbarten Knoten die alternierende Farbe zu
					queue.Enqueue(i); // Fügt den Knoten der Queue hinzu
				}
				else
				{
					if (graph[index, i] == 1 && coloredVertices[i] == coloredVertices[index]) // Wenn die Knoten verbunden sind und dieselbe Farbe haben, wird false zurückgegeben
					{
						return false;
					}
				}
			}
		}
		return true; // Wenn alle benachbarten Knoten alternierende Farben haben, wird true zurückgegeben
	}
	
	// Diese Methode gibt true zurück, wenn der Graph bipartit ist, sonst false
	private static bool IsBipartite(int[,] graph, int numberOfVertices)
	{
		int[] coloredVertices = new int[numberOfVertices]; // Deklariert ein Array für die Farben der Knoten
		for (int i = 0; i < numberOfVertices; i++) // for-Schleife, die die Knoten durchläuft
		{
			coloredVertices[i] = -1; // Initialisiert die Knoten mit -1, sodass die Knoten am Anfang nicht gefärbt sind
		}
		// Prüfung für die Komponenten des Graphen
		for (int i = 0; i < numberOfVertices; i++) // for-Schleife, die die Knoten durchläuft
		{
			if (coloredVertices[i] == -1 && !IsBipartite(graph, i, coloredVertices)) // Wenn der Knoten noch nicht gefärbt ist und die Komponente mit diesem Startknoten nicht bipartit ist, wird false zurückgegeben
			{
				return false;
			}
		}
		return true; // Wenn alle Komponenten bipartit sind, wird true zurückgegeben
	}
	
	// Hauptmethode, die das Programm ausführt
	public static void Main(String[] args)
	{
		// Deklariert und initialisiert ein zweidimensionales Array für die Adjazenzmatrix eines ungerichteten Graphen mit 4 Knoten
		int[,] graph = {{ 0, 1, 0, 1 },
			{1, 0, 1, 0},
			{0, 1, 0, 1},
			{1, 0, 1, 0},
		};
		int numberOfVertices = (int) graph.GetLongLength(0); // Variable für die Anzahl der Knoten
		if (IsBipartite(graph, numberOfVertices)) // Aufruf der Methode
		{
			Console.WriteLine("Der Graph ist bipartit."); // Ausgabe auf der Konsole
		}
		else
		{
			Console.WriteLine("Der Graph ist nicht bipartit."); // Ausgabe auf der Konsole
		}
		
		Console.ReadLine();
	}
}

Siehe auch

• Matching (Graphentheorie)
• Petri-Netz
• Sekretärinnenproblem

Literatur

• Frank Gurski, Irene Rothe, Jörg Rothe, Egon Wanke: Exakte Algorithmen für schwere Graphenprobleme, Springer-Verlag, Berlin Heidelberg, 2010, ISBN 978-3-642-04499-1.
• Sven Krumke, Hartmut Noltemeier: Graphentheoretische Konzepte und Algorithmen, Vieweg+Teubner Verlag, 2012, ISBN 978-3-8348-1849-2.

Weblinks

Wikiversity: Eine Vorlesung über bipartite Graphen im Rahmen eines Kurses zur diskreten Mathematik – Kursmaterialien

Commons: Bipartiter Graph – Sammlung von Bildern, Videos und Audiodateien

• Bipartiter Graph. In: Springer Lexikon der Mathematik.