Frequenzspektrum
Das Frequenzspektrum, meist einfach Spektrum, eines Signals gibt dessen Zusammensetzung aus verschiedenen Frequenzen an. Im Allgemeinen ist das Frequenzspektrum eine komplexwertige Funktion. Ihr Betrag heißt Amplitudenspektrum, sein Phasenwinkel heißt Phasen(winkel)spektrum.
Der Begriff Frequenzspektrum umfasst viele unterschiedliche Phänomene aus allen Bereichen der Physik wie aus der Optik, der Akustik, der Elektrodynamik oder der Mechanik.
- Licht besteht aus Wellen verschiedener Frequenzen. Mit dem Spektrum des Lichts verändert sich meist seine Farbe, siehe Farbwahrnehmung.
- Die Frequenz eines Tones bestimmt seine Tonhöhe. Unter anderem das Frequenzspektrum des Schalls charakterisiert den Klang eines Musikinstruments oder einer menschlichen Stimme.
- Das Frequenzgemisch eines Rundfunksignals enthält die Bild- und Toninformation.
- Die Frequenz einer mechanischen Schwingung bestimmt, wie oft sich die Schwingung in einer bestimmten Zeit wiederholt. Eine komplizierte mechanische Schwingung ist beispielsweise die Auslenkung eines Seismographen bei einem Erdbeben. Sie setzen sich aus Schwingungen verschiedener Frequenzen zusammen.
Das Frequenzspektrum eines Signals lässt sich aus dem zugrundeliegenden Signal durch Anwendung der Fouriertransformation berechnen. Die Darstellung im Frequenzbereich dient in Physik und Technik dazu, physikalische Vorgänge einfacher zu beschreiben als durch Funktionen der Zeit oder des Ortes.
Frequenzspektrum eines Zeitsignals[Bearbeiten | Quelltext bearbeiten]
Aufgrund der häufigen Verwendung wird zunächst die Klasse der sogenannten Zeitsignale beschrieben. Dem Frequenzspektrum eines Zeitsignals liegt die Anschauung zugrunde, dass sich ein von der Zeit abhängiges Signal x(t) mithilfe der Transformationsregeln von Fourierreihe bzw. Fouriertransformation als eine Summe oder ein Integral von komplexen Exponentialfunktionen verschiedener Frequenzen zusammensetzen lässt. Die komplexen Exponentialfunktionen heißen in diesem Zusammenhang „Aufbaufunktionen“[1]. Das Frequenzspektrum beschreibt, mit welcher Wichtung (d. h. Stärke) die zu der jeweiligen Frequenz zugehörige Aufbaufunktion in das Gesamtsignal eingeht. Zur rechnerischen Darstellung der Signalsynthese werden die Formeln zur Fourier-Rücktransformation dargestellt. Dazu ist es erforderlich zu unterscheiden, welche Art von Signal vorliegt.
Periodisches Signal mit diskretem Spektrum[Bearbeiten | Quelltext bearbeiten]
Ist das Signal eine zeitkontinuierliche periodische Funktion mit der Periodendauer , so lautet die zugehörige Gleichung:
Die Gleichung beschreibt das Signal x(t) als eine Summe von komplexen Exponentialschwingungen der Frequenzen . Als Spektrum des Signals x bezeichnet man die Funktion
mit der Grundfrequenz . Die Zahl steht stellvertretend für das n-fache der Grundfrequenz. Die komplexe Exponentialschwingung kann durch die Gleichung beschrieben werden. Da das Spektrum nur für die diskreten Frequenzen definiert ist, spricht man von einem diskreten Spektrum bzw. von einem Linienspektrum.
Nichtperiodisches Signal mit kontinuierlichem Spektrum[Bearbeiten | Quelltext bearbeiten]
Ist das Signal x(t) eine nichtperiodische zeitkontinuierliche Funktion mit endlicher Signalenergie, so lautet die zugehörige Transformationsgleichung:
Als Spektrum des Signals bezeichnet man in diesem Fall die Funktion
Da das Spektrum für alle reellwertigen Frequenzen definiert ist, spricht man auch von einem sogenannten kontinuierlichen Spektrum. Das Spektrum der kontinuierlichen Fouriertransformation lässt sich als Grenzfall des Linienspektrums der Fourierreihe für den Grenzübergang einer unendlich großen Signal-Periodendauer darstellen.
Erläuterungen und weitere Signalklassen[Bearbeiten | Quelltext bearbeiten]
Beide Frequenzspektren sind sowohl für positive, als auch für negative Frequenzen definiert. Für reellwertige Signale x(t) sind die Spektren für positive und negative Frequenzen jedoch voneinander abhängig, und es gilt: . Der Stern kennzeichnet die komplexe Konjugation. In der Regel wird daher das Spektrum negativer Frequenzen nur für komplexwertige Signale angezeigt.
Im Rahmen der Theorie der Fourieranalyse sind auch für weitere Klassen von Signalen Transformationsformeln definiert, beispielsweise für zeitdiskrete, wertkontinuierliche Signale, d. h. abgetastete Analogsignale. Die Begriffe Frequenzspektrum, Amplitudenspektrum und Phasenspektrum werden dabei analog als komplexe Funktion sowie deren Beträge und Phasen definiert. Die Details werden im Artikel über die Fouriertransformation und den darin enthaltenen Verlinkungen dargestellt.
Im Zusammenhang mit nichtperiodischen Leistungssignalen wie Rauschsignalen existiert der Begriff der spektralen Leistungsdichte, der ähnlich wie das Frequenzspektrum ebenfalls die spektrale Zusammensetzung eines Signals beschreibt. Die Besonderheit von nichtperiodischen Leistungssignalen besteht darin, dass sie nicht fouriertransformierbar sind. Das ist daran zu erkennen, dass die zugehörigen Transformationsintegrale divergieren. Trotzdem kann ein Zusammenhang mit dem Begriff der Fouriertransformation hergestellt werden, der für die messtechnische Praxis bedeutend ist. Falls dem Signal ein ergodischer Entstehungsprozess zugrunde liegt, kann man die spektrale Leistungsdichte näherungsweise dadurch ermitteln, dass man ein Teilsignal endlicher Dauer des eigentlich unendlich langen Signals einer Fouriertransformation unterzieht. Das Quadrat der Fouriertransformierten ist dann näherungsweise proportional zur spektralen Leistungsdichte.
Beispiele[Bearbeiten | Quelltext bearbeiten]
Elementare Signale[Bearbeiten | Quelltext bearbeiten]
Die Spektren elementarer Signale sind in den Beschreibungen der zugehörigen Signaltransformationen enthalten, siehe Beispiele zur Fourierreihe und Beispiele zur Fouriertransformation. Beispielhaft sollen mehrere Spektren einfacher Signale angezeigt werden. Das vierte Beispiel zeigt den Einfluss des Phasenspektrums auf ein schmalbandiges Signal.
 |
 |
 |
 |
Amplitudenspektrum eines Audiosignals[Bearbeiten | Quelltext bearbeiten]
Als Beispiel soll das Amplitudenspektrum des folgenden Geigentons betrachtet werden
Das Spektrum des Geigentons ist abhängig von dem Zeitabschnitt, den man zur Analyse wählt. Betrachtet man einen Signalausschnitt, der während des Streichens der Saiten aufgenommen wurde, so erkennt man außer der Grundfrequenz von f0 = 294 Hz deutliche Frequenzanteile der ganzzahligen Vielfachen . Diese lassen sich dadurch erklären, dass die Saite nicht nur in ihrer Grundwelle schwingt, bei der die Saite auf ihrer gesamten Länge eine Auslenkung erfährt, sondern sich außer am Rand zusätzliche Knotenpunkte bei 1/2, 1/3, 2/3, 1/4, 2/4, 3/4, … der Saitenlänge ausbilden. Die Schwingung bei einem Vielfachen des Grundtons heißt im musikalischen Sprachgebrauch Oberton. Die Ausprägung der einzelnen Obertöne wird nicht nur durch die Schwingung der Saite allein, sondern durch die Gesamtanordnung des Instruments (Saite, Resonanzkörper, Saitendruck beim Streichen bzw. Auslenkung beim Zupfen) bestimmt. Im Gegensatz zum Signalausschnitt während des Streichens zeigt der Signalausschnitt, der das Ausklingen des Tones berücksichtigt, keine markanten Obertonanteile auf.

Frequenzspektrum von Licht[Bearbeiten | Quelltext bearbeiten]
Während im Radiobereich des elektromagnetischen Spektrums das Frequenzspektrum noch aus dem zeitlichen Verlauf der elektrischen Feldstärke ermittelt werden kann, ist das im spektralen Bereich von Licht nicht mehr möglich, denn die Frequenzen liegen bei über 100 Terahertz. Übliche Auftragungen optischer Spektren (siehe Spektroskopie) haben als x-Achse oft die Wellenlänge des Lichts oder die Energie der Lichtquanten. Ist es dagegen die Frequenz, so spricht man von einem Frequenzspektrum. Wellenlängenspektren sind am roten Ende breiter, Frequenzspektren am blauen Ende – breiter und flacher, falls das Spektrum als spektrale Intensität pro Einheit der x-Achse dargestellt ist.
Ortsfrequenzspektren[Bearbeiten | Quelltext bearbeiten]
Hängt das zugrundeliegende Signal s nicht von der Zeit t, sondern von Koordinaten des Ortes ab, so spricht man von einem sogenannten Ortsfrequenzspektrum. Ortsfrequenzspektren können ein-, zwei- oder dreidimensional sein, je nachdem, ob ein-, zwei- oder dreidimensionale Strukturen analysiert werden. Sie können sowohl einen kontinuierlichen, als auch einen diskreten Definitionsbereich aufweisen.
Beispiele für Strukturen mit kontinuierlichem Definitionsbereich sind
- der Grauwertverlauf entlang einer Linie (eindimensional)
- der Grauwertverlauf einer Schwarz-Weiß-Photographie (zweidimensional)
- die Intensitätsverteilung einer physikalischen Größe im Raum (dreidimensional)
Beispiele für Strukturen mit diskretem Definitionsbereich sind
- der Grauwertverlauf auf diskreten Punkten entlang einer Linie (eindimensional)
- der Grauwertverlauf auf diskreten Punkten einer Schwarz-Weiß-Photographie (zweidimensional), z. B. Pixelgraphik
- die Punktverteilung eines Kristallgitters im Raum
Analog wie bei dem Frequenzspektrum einer Zeitfunktion liegt dem Ortsfrequenzspektrum die Anschauung zugrunde, dass sich das Gesamtsignal s(x,y,z) mithilfe der Transformationsregeln der Fourierreihe bzw. der Fouriertransformation als eine Summe oder ein Integral von komplexen Exponentialfunktionen der Ortsfrequenzen , und zusammensetzen lässt.
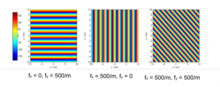
Die Exponentialfunktion lässt sich durch die vom Ort abhängige Signalphase veranschaulichen. Dies wird für den Fall einer zweidimensionalen Transformation in dem nebenstehenden Bild für verschiedene Ortsfrequenzen angezeigt. Man erkennt, dass im Allgemeinen der Vektor die Richtung der maximalen Phasenänderung angibt.
Nichtperiodisches Signal mit kontinuierlichem Spektrum[Bearbeiten | Quelltext bearbeiten]
Ist das Signal s(x,y,z) eine nichtperiodische zeitkontinuierliche Funktion der drei Ortskoordinaten x, y und z, so lautet die zugehörige Transformationsgleichung:
Als Ortsfrequenzspektrum des Signals bezeichnet man die Funktion
Messen des Frequenzspektrums[Bearbeiten | Quelltext bearbeiten]
Das Frequenzspektrum eines elektrischen Signals kann mit einem Spektrumanalysator oder Signalanalysator gemessen werden. Das Spektrum wird dann z. B. mit Hilfe der Fourieranalyse (siehe auch Fouriertransformation) oder nach dem Prinzip des Überlagerungsempfängers aus dem Zeitsignal bestimmt. Als Ergebnis dieser Transformation erhält man die Amplituden der jeweiligen Frequenzanteile A(f) als Funktion der Frequenz f und im Falle zeitlich veränderlicher Amplitudenverteilungen eine Verteilung A(f,t) als Funktion der Frequenz f und der Zeit t.
Charakteristische Spektren[Bearbeiten | Quelltext bearbeiten]
Abhängig von der Anzahl und der Harmonik der enthaltenen Frequenzen ergibt das Spektrum eines (eindimensionalen) Audiosignals einen Klang (Harmonisch), ein Klanggemisch (wenige unharmonische Frequenzen), ein Geräusch (unharmonisch) oder ein Rauschen (alle Frequenzen, statistisch auftretend).
Periodische Signale haben in der Regel ein Linienspektrum, während nichtperiodische Signale, wie Impulse, ein kontinuierliches Frequenzspektrum haben.

Beispiele[Bearbeiten | Quelltext bearbeiten]
- Eine reine Sinusschwingung hat als Frequenzspektrum nur die eine Linie ihrer Frequenz.
- Ein Rechtecksignal der Frequenz f hat ein Linienspektrum mit den Frequenzen f, 3·f, 5·f, …
- Mit einem Impulsgenerator kann man lückenlos alle Oberwellen bis zu extrem hohen Frequenzen erzeugen.
- Ein Ton auf einem Musikinstrument erklingt immer zusammen mit seinen Oberschwingungen. Die Menge aller klingenden Frequenzen ist das Frequenzspektrum dieses Tones.
- Ein amplitudenmodulierter Radio-Sender (z. B. auf Mittelwelle), der Sprache und Musik bis 8 kHz auf 1 MHz überträgt, besitzt ein Frequenzspektrum von 0,992 bis 1,008 MHz.
- Sendet das System elektromagnetische Strahlung aus, so spricht man vom elektromagnetischen Spektrum.
Weitere Bedeutungen[Bearbeiten | Quelltext bearbeiten]
Im erweiterten Sinne bezeichnet Frequenzspektrum eine Auflistung von Frequenzen, die in Bezug auf eine bestimmte Betrachtungsweise zusammen gesehen werden müssen, z. B. das Frequenzspektrum der Radio- und Fernseh-Kanäle; siehe Frequenzband.
Ein Antwortspektrum dient der Bemessung von Bauwerken gegen die Belastung durch Erdbeben.
Siehe auch[Bearbeiten | Quelltext bearbeiten]
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Rüdiger Hoffmann: Signalanalyse und -erkennung: Eine Einführung für Informationstechniker, Springer, 1998, S. 69. Zitat im Zusammenhang mit der komplexen Fourierreihe: „Die Reihe kann als orthogonale Entwicklung der Funktion x nach dem System von Aufbaufunktionen interpretiert werden, […]“
Literatur[Bearbeiten | Quelltext bearbeiten]
- Curt Rint: Handbuch für Hochfrequenz- und Elektro-Techniker, Band 2. 13. Auflage, Hüthig und Pflaum Verlag GmbH, Heidelberg 1981, ISBN 3-7785-0699-4.
- Gregor Häberle, Heinz Häberle, Thomas Kleiber: Fachkunde Radio-, Fernseh- und Funkelektronik. 3. Auflage, Verlag Europa-Lehrmittel, Haan-Gruiten 1996, ISBN 3-8085-3263-7.
- Horst Stöcker: Taschenbuch der Physik. 4. Auflage, Verlag Harry Deutsch, Frankfurt am Main 2000, ISBN 3-8171-1628-4.
- Thomas Görne: Tontechnik. 1. Auflage, Carl Hanser Verlag, Leipzig 2006, ISBN 3-446-40198-9.





























