Katalytisch perfekte Enzyme
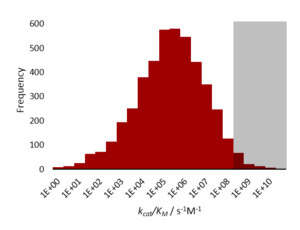
Ein katalytisch perfektes Enzym oder auch kinetisch perfektes Enzym ist ein Enzym, das so effizient katalysiert, dass bei fast jedem Zusammentreffen von Enzym und entsprechendem Substrat eine katalytische Reaktion abläuft. Der kcat/Km-Faktor eines solchen Enzyms liegt in der Größenordnung von 108 bis 109 M−1 s−1. Somit ist die Reaktion von Substrat und Enzym nur noch durch die Diffusionsgeschwindigkeit begrenzt.
Beispiele für katalytisch perfekte Enzyme sind zum Beispiel Triosephosphatisomerase, Carboanhydrase, Acetylcholinesterase, Katalase, Fumarase, β-Lactamase und Superoxiddismutase.
Geschichte[Bearbeiten | Quelltext bearbeiten]
Eine Theorie, die eine diffusionskontrollierte Reaktion beschreibt, wurde von Robert A. Alberty, Gordon Hammes und Manfred Eigen aufgegriffen, um den Höchstwert für die katalytische Effizienz einer Enzym-Substrat-Reaktion herauszufinden. Dieser Wert wird durch den kcat/Km-Faktor beschrieben. Laut deren Untersuchungen lag der Höchstwert bei 109 M−1 s−1.[2][3]
Im Jahr 1972 wurde beobachtet, dass die Dehydratation von Kohlensäure durch die α-Carboanhydrase katalysiert wird, wobei der kcat/Km-Faktor bei 1,5·1010 M−1 s−1 lag, welches den experimentell bestimmten Wert von Alberty, Hammes und Eigen deutlich übertraf.
Kuo-Chen Chou und seine Mitarbeiter perfektionierten das vorherige Modell von Alberty, Hammes und Eigen, indem sie den Spatial-Faktor und den Kraftfeld-Faktor zwischen dem Enzym und seinem Substrat mit berücksichtigten. Somit lag der genauere Höchstwert nun bei 1010 M−1 s−1.[4][5][6] Mit diesem Modell kann die überraschend hohe Reaktionsrate erklärt werden.
Mechanismus[Bearbeiten | Quelltext bearbeiten]
Manche Enzyme jedoch zeigen eine Kinetik, die schneller abläuft, als die Diffusionsgeschwindigkeit, was auf den ersten Blick unmöglich erscheint. Um dieses Phänomen zu erklären, wurden verschiedene Mechanismen vorgeschlagen:
Von einigen Enzymen nimmt man an, dass sie die Katalyse beschleunigen, indem sie ihre Substrate an sich „heranziehen“ und sie mit elektrischen Feldern ausrichten. In Anlehnung an Circe, eine Zauberin aus der griechischen Mythologie, die der Sage nach Odysseus’ Männer in ihr Haus lockte und dort in Schweine verwandelte, hat William P. Jencks hierfür den Begriff Circe-Effekt geprägt.[7] Eine andere Theorie schlägt einen quantenmechanischen Ansatz vor, wobei mithilfe des Tunneleffektes ein Proton oder ein Elektron eine Potentialhürde durchqueren kann, jedoch wird dieser Ansatz zumindest für Protonen widersprüchlich betrachtet.[8][9] Jedoch wurde ein Tunneleffekt für Protonen bei Tryptamin beobachtet.[10] Aufgrund dieser Tatsache drängt sich die Vermutung auf, der Vorgang der Enzymkatalyse könnte besser beschrieben werden, wenn man den Durchtritt durch eine Potentialhürde annimmt, im traditionellen Modell muss ein Substrat eine bestimmte Aktivierungsenergie überschreiten, um seinen Potentialtopf zu verlassen.
Alberty-Hammes-Eigen-Modell (AHE-Modell)[Bearbeiten | Quelltext bearbeiten]

(b) Chou-Modell
E = Enzym
S = Substrat
Zur Berechnung der Geschwindigkeitskonstante beim AHE-Modell wird folgende Gleichung verwendet, die auf der Debye-Smoluchowski-Theorie basiert:
| Geschwindigkeitskonstante im AHE-Modell | |
| Diffusionskoeffizient, | |
| Avogadro-Konstante | |
| Reaktionsradius (Summe aus dem Radius der „aktiven Halbkugel“ und einem Substratmolekül, dabei ist r0 = 5 Å) | |
| Interaktionspotenzial zwischen einem Substratmolekül und dem aktiven Zentrum eines Enzyms | |
| Boltzmann-Konstante | |
| Absolute Temperatur |
Das aktive Zentrum wird als Halbkugel betrachtet. Es beschreibt, dass alle Substrate, die sich in entgegengesetzter Richtung des Enzyms bewegen, durch ein elektrisches Feld in Richtung des außerhalb lokalisierten aktiven Zentrums ausgerichtet und angezogen werden. Das Hauptprotein, welches als „aktive Halbkugel“ repräsentiert wird, stellt eine Diffusionsbarriere dar, das den Diffusionsstrom und die molekularen Kräfte reguliert. Somit stellt dieses Modell eine besondere Form der diffusionskontrollierten Reaktion dar, und zwar die halbkugelsymmetrische Diffusion. Es wurde bewiesen, dass nach dem Alberty-Hammes-Eigen-Modell die Van-der-Waals-Kräfte zu gering sind (U0 < 3 kT), da sich das aktive Zentrum außerhalb befindet und die Wechselwirkungen zwischen dem aktiven Zentrum und dem Substrat dezimiert werden, was dazu führt, dass das Hauptprotein als eine Art „Mauer“ fungiert und somit den Durchfluss der Substratmoleküle zum aktiven Zentrum blockiert und die enzymatische Umsetzung verlangsamt wird.[11]
Chou-Modell[Bearbeiten | Quelltext bearbeiten]
Zur Berechnung der Geschwindigkeitskonstante beim Chou-Modell wurde folgende Gleichung hergeleitet:
| Geschwindigkeitskonstante im Chou-Modell | |
| Diffusionskoeffizient, | |
| Avogadro-Konstante | |
| Hydrodynamischer Radius des Enzyms | |
| Enzymeinheit | |
| Boltzmann-Konstante | |
| Absolute Temperatur | |
| Verhältnis der Konzentration der Substratmoleküle auf der ganzen Oberfläche eines Enzymmoleküls zur Massenkonzentration |
Beim Chou-Modell wird das Kraftfeld und der geometrische Effekt mit einkalkuliert. Der Geschwindigkeitsfaktor beim Chou-Modell ist höher als beim Alberty-Hammes-Eigen-Modell, da die Van-der-Waals-Kräfte größer sind. Beim Chou-Modell liegen die Van-der-Waals-Kräfte bei über 3 kT, da sich das aktive Zentrum innerhalb des Enzyms befindet und somit eine erhöhte Wechselwirkung mit dem Substrat induziert, was dazu führt, dass das Hauptprotein als „Beschleuniger“ fungiert und somit die Strömung der Substratmoleküle zum aktiven Zentrum beschleunigt wird. Dabei werden alle Substrate, die sich in der Nähe des Enzyms befinden, durch das elektrische Feld in Richtung des innerhalb lokalisierten aktiven Zentrums ausgerichtet und angezogen.[11]
Evolution[Bearbeiten | Quelltext bearbeiten]
Aufgrund der natürlichen Selektion existieren nicht viele katalytisch perfekte Enzyme. Eine Erhöhung der katalytischen Reaktionsgeschwindigkeit wäre nur vorteilhaft, wenn diese nicht die Diffusionsgeschwindigkeit übertrifft. Somit stellt die Diffusionsgeschwindigkeit des Enzyms eine physische Einschränkung der Evolution dar und lässt sich in einer Fitnesslandschaft als globales Maximum darstellen. Eine Fitnesslandschaft stellt den Zusammenhang zwischen dem Genotyp und der reproduktiven Fitness, also der Anzahl der Nachkommen eines Individuums in seiner gesamten Lebenszeit (reproductive success), dar. Je höher die Landschaft ist, desto höher ist die Replikationsrate und somit auch die Fitness. Bei Lebewesen korreliert die Replikationsrate mit der Reproduktionsrate. Daher geht man davon aus, dass perfekte Enzyme durch zufällige Mutationen entstanden sind und sich anschließend ausgebreitet haben oder die erhöhte Reaktionsgeschwindigkeit war für einen „Vorfahren“ des Enzyms als Teil von einem anderen Reaktionsmechanismus von Vorteil.[1][12]
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ a b Arren Bar-Even, Elad Noor: The Moderately Efficient Enzyme: Evolutionary and Physicochemical Trends Shaping Enzyme Parameters. In: Biochemistry. 50. Jahrgang, Nr. 21, 31. Mai 2011, S. 4402–4410, doi:10.1021/bi2002289, PMID 21506553 (englisch).
- ↑ Robert A. Alberty, Gordon G. Hammes: Application of the Theory of Diffusion-controlled Reactions to Enzyme Kinetics. In: The Journal of Physical Chemistry. 62. Jahrgang, Nr. 2, Februar 1958, S. 154–159, doi:10.1021/j150560a005 (englisch).
- ↑ Manfred Eigen, Gordon G. Hammes: Advances in Enzymology and Related Areas of Molecular Biology. Wiley-Blackwell, Hoboken (New Jersey) 1963, ISBN 978-0-470-12270-9, S. 1–38.
- ↑ Kuo-Chen Chou, Shou-Ping Jiang: Studies on the rate of diffusion-controlled reactions of enzymes. Spatial factor and force field factor. In: Scientia Sinica. 27. Jahrgang, Nr. 5, 6. März 1974, S. 664–680, PMID 4219062 (englisch, Fehler (Seite nicht mehr abrufbar. Suche in Webarchiven)). Info: Der Link wurde automatisch als defekt markiert. Bitte prüfe den Link gemäß Anleitung und entferne dann diesen Hinweis.
- ↑ Kuo-Chen Chou: The kinetics of the combination reaction between enzyme and substrate. In: Scientia Sinica. 19. Jahrgang, Nr. 4, 276, S. 505–528, PMID 824728 (englisch, Fehler ( des vom 30. Januar 2016 im Internet Archive) [abgerufen am 30. Januar 2016]). Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.
- ↑ Zi-Cai Li, Guo-Cheng Zhou: The quantitative relations between diffusion-controlled reaction rate and characteristic parameters in enzyme-substrate reaction systems. I. Neutral substrates. In: Scientia Sinica. 19. Jahrgang, Nr. 1, S. 117–136, PMID 1273571 (englisch, Fehler ( des vom 30. Januar 2016 im Internet Archive) [abgerufen am 30. Januar 2016]). Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.
- ↑ Stryer: Biochemie. 7. Auflage. Springer-Verlag, Berlin/Heidelberg 2013, ISBN 978-3-8274-2988-9, S. 238.
- ↑ Mireia Garcia-Viloca, Jiali Gao, Martin Karplus und Donald G. Truhlar: In: Science. 9. Januar 2004, Band 303, Nr. 5655, S. 186–195.
- ↑ Mats M. H. Olsson, Per E. M. Siegbahn und A. Warshel: In: Journal of the American Chemical Society. 10. März 2004. Band 126, Nr. 9, S. 2820–2828.
- ↑ L. Masgrau, A. Roujeinikova, L. O. Johannissen, P. Hothi, J. Basran, K. E. Ranaghan, A. J. Mulholland, M. J. Sutcliffe, N. S. Scrutton und D. Leys: Atomic Description of an Enzyme Reaction Dominated by Proton Tunneling. In: Science. 312. Jahrgang, Nr. 5771, 2006, S. 237–241, PMID 16614214.
- ↑ a b Gua-Qiang Zhou, Wei-Zhu Zhong: Diffusion-controlled reactions of enzymes. A comparison between Chou's model and Alberty-Hammes-Eigen's model. In: Eur J Biochem. 128. Jahrgang, Nr. 2–3, 15. November 1982, S. 383–387, doi:10.1111/j.1432-1033.1982.tb06976.x, PMID 7151785 (englisch).
- ↑ Kostyčev Sergej Pavlovič: Lehrbuch der Pflanzenphysiologie: Erster Band: Chemische Physiologie. Springer-Verlag, 2013, S. 567 (Volltext in der Google-Buchsuche).
![{\displaystyle \mathrm {{\mathit {k}}_{AHE}={\frac {2\pi {\mathit {D}}{\mathit {N}}_{A}}{1000\int \limits _{{\mathit {r}}_{0}}^{\infty }\exp \,[{\mathit {U}}\!({\mathit {l)}}/{\mathit {kT}}]\,{\frac {d{\mathit {l}}}{{\mathit {l}}^{2}}}}}\,(M^{-1}\,s^{-1})} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a24463700ad29e0b91a999779a4c540b17abb94)








![{\displaystyle \mathrm {{\mathit {k}}_{lim}={\frac {4\pi {\mathit {D}}{\mathit {N}}_{A}}{1000\int \limits _{{\mathit {R}}_{0}}^{x}e^{\mathit {U/kT}}\,{\frac {d{\mathit {r}}}{{\mathit {r}}^{2}}}}}[1-{\tilde {g}}e^{{\mathit {U}}({\mathit {R}}_{0})/{\mathit {kT}}}]\,(M^{-1}\,s^{-1})} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1ea295db6f9b824aacd35adfff0193bca8f3515)



