Kreisevolvente

Kreisevolvente

Ineinander greifende Zahnradzähne
Autor: Claudio Rocchini

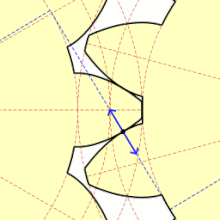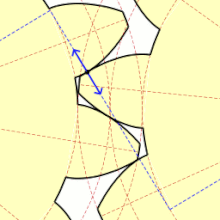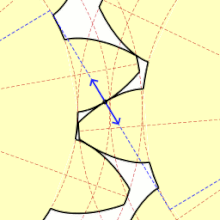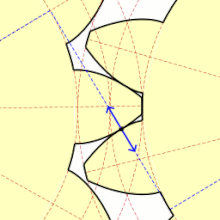
Eine Kreisevolvente ist eine ebene geometrische Kurve, eine spezielle Evolvente mit einem Kreis als Evolute. Sie hat erhebliche Bedeutung bei der Evolventenverzahnung im Maschinenbau, wo sie als Zahnflanke von Zahnrädern auftritt. Anschaulich ist sie die Bahn eines Fadenendes, wenn man den Faden gestrafft vom Umfang eines Kreises abwickelt.

Eigenschaften

Die Kreisevolvente ist eine Spirale mit konstantem Windungsabstand. Diese Eigenschaft wird oft fälschlicherweise der archimedischen Spirale zugeschrieben. Die Kreisevolvente ist damit ihre eigene Parallelkurve.

Mathematische Darstellung

Die Parameterdarstellung der Kreisevolvente des Einheitskreises, die bei $(1,0)$ mit Anfangssteigung ${\tfrac {\mathrm {d} y}{\mathrm {d} x}}|_{(1,0)}=0$ startet, lautet mit $t\in \mathbb {R} _{0}^{+}$:

$x(t)=\cos(t)+t\sin(t)$

$y(t)=\sin(t)-t\cos(t)$

Dabei ist der Parameter $t$ die Länge des abgewickelten Stück Fadens, also die (abgewickelte) Bogenlänge auf dem zugrunde liegenden Einheitskreis. Für die Bogenlänge der konstruierten Evolvente gilt

$s={\tfrac {1}{2}}t^{2}$

und für ihre Krümmung

$\kappa ={\tfrac {1}{t}}$,

womit der Parameter $t$ auch gleichzeitig ihr Krümmungsradius ist. In Polarkoordinaten lautet ihre Darstellung:

$r(t)={\sqrt {1+t^{2}}}$

$\varphi (t)=t-\arctan(t)$

Alle anderen geometrisch kongruenten Kreisevolventen gehen aus ihr durch Drehung um den Koordinatenursprung und Verschiebung hervor. Ferner lässt sich die Kurvendefinition auch auf alle $t<0$ natürlich fortsetzen, wobei alle Formeln zur Kurvengeometrie bis auf die der Bogenlänge gültig bleiben, welche zu $s={\tfrac {\operatorname {sgn}(t)}{2}}t^{2}$ verallgemeinert wird. Geometrisch erhält die ursprüngliche Kurve einen weiteren Ast, der durch Spiegelung ihrer selbst an der x-Achse erzeugt wird.

Siehe auch

Commons: Kreisevolvente – Sammlung von Bildern, Videos und Audiodateien

• Involut-Funktion

Literatur

• Mark Ja. Vygodskij: Höhere Mathematik griffbereit: Definitionen Theoreme Beispiele. Springer, 2013, ISBN, S. 729–731
• Joachim Erven, Dietrich Schwägerl: Mathematik für Ingenieure. Walter de Hruyter, 4. Auflage 2011, ISBN 978-3-486-70796-0, S. 216-217

Weblinks

• Nora Rebecca Thomas: Geometrische Eigenschaften von Kurven. Staatsexamensarbeit, Uni Main, 2010, S. 22–28