Processing (Seismik)

Das Processing ist die Aufbereitung seismischer Daten bei reflexionsseismischen Untersuchungen. Sie wird durchgeführt, um aus den Rohdaten eines seismischen Experiments ein sinnvolles geologisches Abbild des Untergrundes zu erhalten. Bei einem seismischen Experiment werden Zweiwegelaufzeiten (Two Way Travel Time, TWT) aufgezeichnet, also die Zeit von der Abgabe des Impulses an der seismischen Quelle hinunter zum Reflektor und zurück an die Erdoberfläche zum Geophon. Die Daten müssen so bearbeitet werden, dass aus den Zeitmessungen Informationen zur Tiefe der Reflektoren werden, um erfolgreiche Bohrungen (z. B. bei der Kohlenwasserstoff-Exploration) oder tiefenbezogene Erkenntnisse in der geologischen und geophysikalischen Grundlagenforschung zu ermöglichen.
Preprocessing[Bearbeiten | Quelltext bearbeiten]
Für die anschließende Bearbeitung werden die gemessenen Daten zunächst in Common Midpoint-Gather sortiert.
Das daran anschließende Preprocessing umfasst die analoge Bandpassfilterung des Signals, statische Korrekturen und die Dekonvolution des Signals.
Bandpassfilterung[Bearbeiten | Quelltext bearbeiten]
Der Bandpassfilter besteht aus einem Hochpassfilter und einem Tiefpassfilter. Bei der Digitalisierung des analogen seismischen Signals kann es zu Alias-Effekten kommen. Dazu kommt es, wenn das Abtasttheorem verletzt wurde und man eine zu niedrige Abtastfrequenz gewählt hat. Um dies zu verhindern setzt man einen analogen Tiefpassfilter vor der Abtastung des Signals ein. Außerdem wendet man einen Hochpassfilter an, um Rauschen, Netzbrummen und langperiodische Anteile von Oberflächenwellen zu unterdrücken.
Statische Korrektur[Bearbeiten | Quelltext bearbeiten]
Durch die statische Korrektur wird das seismische Experiment auf ein Bezugsniveau reduziert, da die oberste Schicht des Untergrundes (Verwitterungsschicht) Höhenunterschiede und starke Geschwindigkeitsinhomogenitäten aufweist. Zur Berechnung der statischen Korrektur benötigt man die Mächtigkeit und die seismische Geschwindigkeit der Schicht zwischen dem Bezugsniveau und der Oberfläche. Diese lassen sich mittels Refraktionsseismik an den oberflächennahen Schichten oder einer seismischen Quelle in einem Bohrloch ermitteln. In der marinen Seismik sind statische Korrekturen notwendig um den Einfluss der Gezeiten sowie unterschiedliche Tiefen von Empfängern und Quelle auszugleichen.
Geschwindigkeitsanalyse[Bearbeiten | Quelltext bearbeiten]
| Modell | Geschwindigkeitsinkrement |
|---|---|
| Horizontaler Reflektor | |
| n horizontale Reflektoren | |
| Geneigter Reflektor | |
| Beliebiges Modell |
Der Normal MoveOut (NMO) ist die Abweichung der Laufzeiten von der Einsatzzeit. Die Geschwindigkeitsanalyse muss vor der weiteren Bearbeitung der seismischen Daten erfolgen, um den Normal MoveOut zu bestimmen und zu korrigieren. Die Laufzeitkurve einer seismischen Welle ergibt sich aus . Die MoveOut-Geschwindigkeit beinhaltet sowohl die Art der Welle, als auch die Modellannahme (siehe Tabelle).
Geschwindigkeitsbestimmung[Bearbeiten | Quelltext bearbeiten]
t–Δt-Methode[Bearbeiten | Quelltext bearbeiten]
Die --Methode basiert auf der parabolischen Näherung. Die zugrundeliegende Gleichung ist . Nun trägt man gegen auf und kann aus der Steigung die MoveOut-Geschwindigkeit berechnen.
t2–x2-Methode[Bearbeiten | Quelltext bearbeiten]
Die --Methode ist genauer als die --Methode, da sie auf der Hyperbelnäherung basiert. Man kann die Laufzeitkurve in ein --Diagramm eintragen und die Geschwindigkeit bestimmen. Wie bei der --Methode beträgt die Steigung der Gerade .
Dynamische Korrektur[Bearbeiten | Quelltext bearbeiten]
Die dynamische NMO-Korrektur reduziert die Laufzeitkurve offsetabhängig auf die Einsatzzeit. Für jedes CMP-Gather wird für jedes eine NMO-Korrektur durchgeführt. Dies gibt eine grobe Abschätzung der seismischen Geschwindigkeiten im Untergrund, birgt allerdings Probleme. Die NMO-Korrektur ist eine nicht-lineare Streckung der Zeitachse entlang des Offsets. Entsprechend wird das Signal mit zunehmenden Offset gestreckt (NMO-Stretch) und die Frequenz wird gemindert.
Die Daten werden um den NMO-Stretch korrigiert, indem man einen linearen Filter anwendet, der die Anteile im Gather Null setzt. Die Daten sind nun bereit gestapelt zu werden.
Durchschnittsgeschwindigkeit[Bearbeiten | Quelltext bearbeiten]
Um die Durchschnittsgeschwindigkeit zu ermitteln, versenkt man Geophone in ein Bohrloch und zündet eine seismische Quelle neben dem Bohrloch (vertical seismic profiling). Die Durchschnittsgeschwindigkeit bezeichnet den geometrisch kürzesten Weg von der Quelle zum Reflexionspunkt.
Effektivgeschwindigkeit[Bearbeiten | Quelltext bearbeiten]
Die Effektivgeschwindigkeit (Root Mean Square) bezeichnet den quadratischen Mittelwert der Geschwindigkeit.
Intervallgeschwindigkeit[Bearbeiten | Quelltext bearbeiten]
Die Intervallgeschwindigkeit ergibt sich aus der Dix-Dürbaum-Krey-Formel:
ist die Geschwindigkeit der Schicht zwischen und . Für eine homogene Schicht ist die Schichtgeschwindigkeit und für einen geschichteten Bereich ist die Effektivgeschwindigkeit
Stapelgeschwindigkeit[Bearbeiten | Quelltext bearbeiten]
Die Stapelgeschwindigkeit ergibt zusammen mit der Pseudoeinsatzzeit die Laufzeitkurve
.
Diese Hyperbel nähert sich an die wahre Laufzeitkurve in der Art an, dass die Flächen der positiven und negativen Abweichung sich balancieren. Die Stapelgeschwindigkeit und die Pseudoeinsatzzeit variieren mit dem Offset der Laufzeitkurve.
Automatische Geschwindigkeitsanalyse[Bearbeiten | Quelltext bearbeiten]
Die --Methode muss von Hand ausgeführt werden, sie lässt sich weder automatisieren noch ist sie objektiv. Diese Ansprüche werden jedoch an moderne Processing-Algorithmen gestellt.
Constant Velocity Scan[Bearbeiten | Quelltext bearbeiten]
Es werden konstante Geschwindigkeiten aus einem adäquaten Geschwindigkeitsbereich verwendet, um eine NMO-Korrektur anzuwenden. Anschließend wird für jede Reflexion die Geschwindigkeit ausgewählt, die die MoveOut-Zeiten auf die Einsatzzeit verschiebt. Dies Verfahren muss visuell ausgewertet werden und ist besonders bei schlechtem Rauschabstand sehr subjektiv.
Constant Velocity Stack[Bearbeiten | Quelltext bearbeiten]
Beim Constant Velocity Stack oder Brute Stack werden wieder konstante Geschwindigkeiten aus einem Geschwindigkeitsbereich verwandt um die NMO-Korrektur auf das CMP-Gather anzuwenden. Anschließend werden die einzelnen Spuren des CMP aufsummiert. Durch destruktive Überlagerungen werden Laufzeitkurven, die mit der falschen NMO-Geschwindigkeit korrigiert werden, bei der Summation (Stapelung) ausgelöscht. Sind alle MoveOut-Zeiten in Phase mit der Einsatzzeit, ist die Amplitude der resultierenden Spur am größten und die gewählte Geschwindigkeit optimal.
Dieses Verfahren muss trotzdem noch visuell ausgewertet werden und unterliegt einer gewissen Subjektivität.
Geschwindigkeitsspektrum[Bearbeiten | Quelltext bearbeiten]

Die Berechnung von Geschwindigkeitsspektren automatisiert die Auswahl der Geschwindigkeitsfunktion .
Für jede Einsatzzeit wird für eine Geschwindigkeit die NMO-Korrektur angewandt. Daraufhin wird der Semblance-Koeffizient für ein Zeitfenster um berechnet.
Hierbei bezeichnet N die Anzahl der Spuren im CMP-Gather und M die Anzahl der diskreten Werte in der j-ten Spur. Der Semblance-Koeffizient normiert die Energie der eingehenden Spur auf die Energie aller Spuren, weswegen er nur Werte zwischen 1 und 0 annehmen kann. Diese Berechnung wird für alle and alle wiederholt und in ein -Diagramm eingetragen. Man erhält die Funktion für das Geschwindigkeitsspektrum. Nun kann automatisiert für jede Reflexion der höchste Semblance-Koeffizient ausgewählt werden, der die optimale Stapelgeschwindigkeit charakterisiert.
Der Semblance-Koeffizient ist ein Maß für die Kohärenz und wird wegen der hohen Auflösung in Zeit und Geschwindigkeit verwendet.
Ergebnis der Geschwindigkeitsanalyse[Bearbeiten | Quelltext bearbeiten]
Aus der Geschwindigkeitsanalyse und NMO-Korrektur der CMP-Gather mit anschließender Stapelung erhält man eine Zeitsektion aus Lotzeiten, auch Zero-Offset-Sektion oder Stapelsektion genannt. Diese simulieren einen vertikalen Strahleinfall von der Quelle zum Reflektor. Das Datenvolumen wird um den Faktor des Überdeckungsgrades des CMP-Gathers reduziert.
Migration[Bearbeiten | Quelltext bearbeiten]
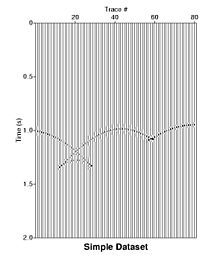
Migration (von lateinischen: migratio, Wanderung, Übersiedlung) in der Seismik bezeichnet Verfahren zur Erstellung eines Untergrundbildes aus dem gemessenen Wellenfeld an der Oberfläche.
Ziel der Migration ist es, aus den Reflexionen im Untergrund ein geologisches Abbild des Untergrundes mit den korrekten Neigungen, Längen und Positionen der Reflektoren zu erstellen.
Motivation[Bearbeiten | Quelltext bearbeiten]
CMP-Gather können Triplikationen und andere kreuzende Schichten beinhalten, die geologisch nicht vorkommen. Zudem werden diese Zeiten in Tiefen migriert um exakte Bohrungen zu ermöglichen.
Migrationsarten[Bearbeiten | Quelltext bearbeiten]
Man kann verschiedene Kriterien zur Unterscheidung der Migration heranziehen.
Zum einen wird zwischen der Zeitmigration in den -Raum und der Tiefenmigration in den -Raum unterschieden. Die Tiefenmigration reagiert dabei empfindlicher auf Fehler im Geschwindigkeitsmodell des Untergrundes, liefert im Gegensatz zur Zeitmigration dafür ein authentisches Abbild des Untergrundes. Zum anderen kann man zwischen der Prestack- und der Poststack-Migration unterscheiden. Die Poststack-Migration wird nach der Geschwindigkeitsanalyse und Stapelung gemacht. Die Prestack-Migration findet vor der Geschwindigkeitsanalyse und der Stapelung statt, um auch Amplituden der eingehenden Signale zu berücksichtigen.
Durch speziellere Prestack-Migrationen können Aussagen über die Reflexionskoeffizienten im Untergrund getroffen werden.
Siehe auch[Bearbeiten | Quelltext bearbeiten]
Literatur[Bearbeiten | Quelltext bearbeiten]
- O. Yilmaz: Seismic data processing. Society of Exploration Geophysicists, Tulsa 2001, ISBN 0-931830-40-0.
- Dirk Gajewski: Vorlesungsskript: Angewandte Geophysik II. (PDF; 32,5 MB) Hamburg 2010, abgerufen am 26. Februar 2010.
- Claudia Vanelle: Vorlesungsskript: Migration. Hamburg 2009; Kapitel 1 (PDF) Kapitel 2 (PDF) Kapitel 3 (PDF); abgerufen am 26. Februar 2010.




























