„Baryzentrische Koordinaten“ – Versionsunterschied
| [gesichtete Version] | [gesichtete Version] |
→Baryzentrische Koordinaten in der Dreiecksgeometrie: Tippfehler korrigiert Markierungen: Mobile Bearbeitung Bearbeitung von einer mobilen Anwendung Bearbeitung mit Android-App |
Neue Version |
||
| Zeile 2: | Zeile 2: | ||
{{QS-Mathematik}} |
{{QS-Mathematik}} |
||
[[Datei:Baryzentr-ko-def-2d.svg|mini|hochkant=1.25|Baryzentrische Koordinaten eines Punktes (blau) als Verhältnis dreier Massen in den Ecken eines Dreiecks (rot), deren [[Massenmittelpunkt|Schwerpunkt]] (Massenmittelpunkt) der Punkt ist.<br>Sind alle Massen gleich, ist der Punkt der [[Geometrischer Schwerpunkt|geometrische Schwerpunkt]] des Dreiecks und hat die Koordinaten <math>(1:1:1)</math>]] |
|||
'''Baryzentrische Koordinaten''' (auch '''homogene baryzentrische Koordinaten''') dienen in der [[Lineare Algebra|linearen Algebra]] und in der [[Geometrie]] dazu, die Lage von [[Punkt (Geometrie)|Punkten]] in Bezug auf eine gegebene [[Strecke (Geometrie)|Strecke]], ein gegebenes [[Dreieck]], ein gegebenes [[Tetraeder]] oder allgemeiner ein gegebenes [[Simplex (Mathematik)|Simplex]] zu beschreiben. |
|||
{{Überarbeiten}} |
|||
Ebene baryzentrische Koordinaten eines Punktes <math>P</math> kann man sich als Verhältnisse von drei Massen <math>m_1,m_2,m_3</math> vorstellen, die sich in den Ecken eines vorgegeben Dreiecks befinden und deren [[Massenmittelpunkt|Schwerpunkt]] <math>P</math> ist (siehe Bild). Da es dabei nur auf Verhältnisse ankommt, schreibt man <math>(m_1:m_2:m_3)</math>. |
|||
{{Belege fehlen}} |
|||
Baryzentrische Koordinaten wurden zuerst von [[August Ferdinand Möbius|A.F. Möbius]] 1827 in seinem Buch ''Der baryzentrische Calcul'' eingeführt.<ref>Max Koecher, Aloys Krieg: ''Ebene Geometrie.'' Springer-Verlag, Berlin 2007, ISBN 978-3-540-49328-0, S. 76.</ref> Sie sind ein Spezialfall [[Homogene Koordinaten|homogener Koordinaten]]. Ein wesentlicher Unterschied zu den üblichen homogenen Koordinaten, z. B. in der Ebene, ist die Beschreibung der Ferngerade durch die Gleichung <math>x_1+x_2+x_3=0</math> statt durch <math>x_3=0</math>. |
|||
'''Baryzentrische Koordinaten''' (auch '''homogene baryzentrische Koordinaten''') dienen in der [[Lineare Algebra|linearen Algebra]] und in der [[Geometrie]] dazu, die Lage von [[Punkt (Geometrie)|Punkten]] in Bezug auf eine gegebene [[Strecke (Geometrie)|Strecke]], ein gegebenes [[Dreieck]], ein gegebenes [[Tetraeder]] oder allgemeiner ein gegebenes [[Simplex (Mathematik)|Simplex]] zu beschreiben. Der Punkt wird dargestellt durch die Koeffizienten einer Affinkombination (also einer [[Linearkombination]] von Punkten, bei der die Summe der Koeffizienten 1 ist). |
|||
Insbesondere in der [[Dreiecksgeometrie]] spielen die baryzentrischen Koordinaten, neben den [[Trilineare Koordinaten|trilinearen Koordinaten]], eine wesentliche Rolle. Überall, wo es um Verhältnisse von Strecken geht, wie zum Beispiel in dem [[Satz von Ceva]], sind sie ein hervorragendes Werkzeug. Aber nicht nur in der Geometrie, sondern auch im Bereich des [[Computer-aided design|Computer-aided Design]] verwendet man sie zur Erzeugung von dreieckigen Flächenstücken, den dreieckigen [[Bézierfläche|Bezierflächen]]. |
|||
Sie sind ein Spezialfall [[Homogene Koordinaten|homogener Koordinaten]]. |
|||
<ref>Josef Hoschek, Dieter Lasser: ''Grundlagen der geometriechen Datenverarbeitung.'' Teubner-Verlag,, 1989, ISBN 3-519-02962-6, S. 243.</ref><ref>Gerald Farin: ''Curves and Surfeces for Computer Aided Geometric Design.'' Academic Press, 1990, ISBN 0-12-249051-7, S. 20.</ref> |
|||
In dem Abschnitt ''Einführung baryzentrischer Koordinaten'' werden die Koordinaten mit <math>(m_1:m_2), (m_1:m_2:m_3)</math> bezeichnet, um immer wieder an ihre Beziehung zu Massen und deren Schwerpunkt zu erinnern, was oft eine Hilfe ist. Erst im Abschnitt ''Allgemeine baryzentrische Koordinaten'' werden die in der Mathematik üblichen Bezeichnungen benutzt. |
|||
== Beispiele == |
|||
== Einführung baryzentrischer Koordinaten == |
|||
=== Punkte einer Geraden === |
|||
=== 2 Massen auf einer Gerade === |
|||
[[Datei:BaryzKoord1.png|Normierte baryzentrische Koordinaten einiger Punkte in Bezug auf die Strecke [AB]|center]] |
|||
[[Datei:Baryzentr-ko-mechanik.svg|mini|hochkant=1.5|Schwerpunkt zweier Massen]] |
|||
Der Schwerpunkt zweier Massen <math>m_1,m_2</math>, die auf der x-Achse an den Stellen <math>x_1,x_2</math> platziert sind, ist der Punkt <math>x_s</math>, an dem die Masse <math>m_1+m_2</math> angebracht werden muss, so dass sie dasselbe [[Drehmoment]] bezüglich irgendeines Punktes bewirkt. Bezgl. des Nullpunktes muss also gelten <ref>Christian Gerthsen: ''Physik'', Springer-Verlag, 1963, S. 37</ref>. |
|||
:'''(G1)''' <math>\ (m_1+m_2)x_s=m_1x_1+m_2x_2 \; .</math> Auflösen ergibt |
|||
:'''(S1)''' <math>\ x_s=\frac{m_1x_1+m_2x_2}{m_1+m_2} \; .</math> |
|||
;Eigenschaften des Schwerpunkts |
|||
Gegeben sei eine Strecke <math>\left[AB\right]</math>. Für jeden Punkt der [[Gerade]]n <math>AB</math> lassen sich baryzentrische Koordinaten angeben, wobei diese allerdings nicht eindeutig festgelegt sind. Um Eindeutigkeit zu erreichen, verwendet man oft ''normierte baryzentrische Koordinaten,'' das heißt baryzentrische Koordinaten, deren Summe gleich 1 ist. Die in der Skizze für einige Beispielpunkte angegebenen baryzentrischen Koordinaten sind normiert. Verzichtet man auf die Normierung, so könnte man beispielsweise den Punkt <math>A</math> durch <math>(5,0)</math> ausdrücken oder den Mittelpunkt von <math>\left[AB\right]</math> durch <math>(1,1)</math>. Allgemein führt die Multiplikation aller Koordinaten mit derselben reellen Zahl (ungleich 0) wieder zu baryzentrischen Koordinaten. |
|||
#Die Lage des Schwerpunkts hängt nicht von der zufälligen Wahl des Nullpunktes und einer Skalierung ab. |
|||
#Die Lage des Schwerpunktes hängt nur von dem Verhältnis <math>m_1:m_2</math> ab. D.h.: Die Massen <math>c m_1,c m_2</math> besitzen denselben Schwerpunkt. |
|||
#Lässt man negative Massen zu, z.B. <math>m_1=1, m_2=-1+\tfrac 1 n</math>, so ergibt sich für <math>n \to \infty</math> die Gesamtmasse <math>m_1+m_2=0</math> und <math>x_s=\infty</math>. |
|||
=== |
=== Baryzentrische Koordinaten einer Gerade === |
||
[[Datei:Baryzentr-ko-gerade.svg|mini|hochkant=2|Baryzentrische Koordinaten auf einer Gerade (unten). Der Mittelpunkt der Strecke <math>X_1,X_2</math> hat die baryzentrischen Koordinaten <math>(1:1)=(\tfrac 1 2:\tfrac 1 2)</math>]] |
|||
Die Beziehung eines Schwerpunktes zu zwei gegebenen Massen erlaubt es, einen beliebigen Punkt <math> x_s </math> der x-Achse als Schwerpunkt zweier in <math>x_1,x_2</math> platzierten Massen <math>m_1,m_2</math> aufzufassen. Allerdings ist diese Zuordnung nicht eindeutig. Die Eindeutigkeit kann man aber mit der Forderung <math>\; m_1+m_2=1\; </math> erzwingen. |
|||
Paare <math>m_1,m_2 </math> von Massen in den fest vorgegebenen Punkten <math>x_1,x_2</math> kann man also als [[homogene Koordinaten]] <math>(m_1:m_2) </math> eines Punktes <math>x_s</math> (des Schwerpunktes der Massen) der x-Achse auffassen. Aufgrund dieser Beziehung, nennt man diese Koordinaten '''baryzentrische Koordinaten''' des Punktes <math>x_s</math>. Der Punkt <math>x_1</math> bzw. <math>x_2</math> hat die homogenen Koordinaten <math>(1:0)</math> bzw. <math>(0:1)</math>. Für den Fernpunkt <math>\infty</math> gilt <math>\;m_1+m_2=0\;</math>. Er hat die baryzentrischen Koordinaten <math>(1:-1)</math>. Man beachte: Bei der üblichen (nicht baryzentrischen) homogenen Koordinatisierung wird der Fernpunkt durch (1:0) beschrieben ! |
|||
In einer [[Ebene (Mathematik)|Ebene]] beziehen sich die baryzentrischen Koordinaten auf ein gegebenes Dreieck. Die in der Skizze eingetragenen Koordinaten sind normiert. |
|||
Falls die Eindeutigkeit durch die Gleichung |
|||
[[Datei:BaryzKoord2.png|Normierte baryzentrische Koordinaten einiger Punkte in Bezug auf ein Dreieck ABC|center]] |
|||
:'''(N1)''' <math>\quad m_1+m_2=1\;</math> |
|||
erzwungen wird, spricht man von '''normierten baryzentrischen Koordinaten'''. |
|||
Ist ein Punkt <math>x_s</math> gegeben, so erhält man seine baryzentrischen Koordinaten durch Auflösen der Gleichgewichtsgleichung '''(G1)''' nach <math>m_1,m_2</math>, was als unterbestimmtes lineares Gleichungssystem nicht eindeutig möglich ist: |
|||
== Allgemeine Definition == |
|||
[[Datei:Baryzentr-ko-gerade-l1l2.svg|mini|hochkant=1.2|baryzentrische Koordinaten als Verhältnis von Strecken]] |
|||
{{Überarbeiten}} |
|||
:'''(B1)''' <math>\;(m_1:m_2)= (x_2-x_s:x_s-x_1)= (l_{\color{red}2}:l_{\color{red}1})\; .</math> |
|||
<math>x_1,\ldots,x_n</math> seien die Eckpunkte eines [[Simplex (Mathematik)|Simplex]] im Vektorraum <math>A</math>. Wenn für einen Punkt <math>p</math> aus <math>A</math> folgende Gleichung erfüllt ist, |
|||
Dabei ist <math>\; l_1=x_s-x_1,\; l_2=x_2-x_s\; .</math> Dieser einfache Zusammenhang der baryzentrischen Koordinaten mit Verhältnissen von Strecken ist der Grund für ihre große Bedeutung in der Dreiecksgeometrie. |
|||
Im normierten Fall wird zur Gleichung '''(G1)''' die Normierungsgleichung '''(N1)''' hinzugenommen, wodurch das LGS für <math>m_1,m_2</math> eindeutig wird. Lösung mit der [[Cramersche Regel|Cramerschen Regel]] liefert |
|||
:<math>(a_1 + \dotsb + a_n) \cdot p = a_1 x_1 + \dotsb + a_n x_n,</math> |
|||
:<math>m_1=\frac{x_2-x_s}{x_2-x_1}, \ m_2=\frac{x_s-x_1}{x_2-x_1}\; </math> und damit die normierten baryzentrischen Koordinaten |
|||
:'''(NB1)''' <math>\ \big(\frac{x_2-x_s}{x_2-x_1}\; :\; \frac{x_s-x_1}{x_2-x_1}\big)=\big(\frac{l_2}{l_1+l_2}:\frac{l_1}{l_1+l_2}\big)\; .</math> |
|||
Der Mittelpunkt <math>\tfrac{x_1+x_2}{2}</math> der Punkte <math>x_1,x_2</math> besitzt die baryzentrischen Koordinaten <math>(1:1)</math> und in normierter Darstellung <math> (\tfrac 1 2:\tfrac 1 2) \; .</math> |
|||
=== 3 Massen in einer Ebene === |
|||
so nennen wir die Koeffizienten <math>(a_1,\ldots,a_n)</math> ''baryzentrische Koordinaten'' von <math>p</math> zu <math>x_1,\ldots,x_n</math>. Die Eckpunkte haben die Koordinaten <math>(1, 0, 0, \ldots, 0), (0, 1, 0, \ldots, 0), \ldots, (0, 0, 0, \ldots, 1)</math>. Baryzentrische Koordinaten sind nicht eindeutig: Für jedes von Null verschiedene <math>b</math> sind <math>(b a_1, \ldots, b a_n)</math> ebenfalls baryzentrische Koordinaten von <math>p</math>. |
|||
Sind in den Ecken eines Dreiecks <math>\; X_1=(x_1,y_1),\;X_2=(x_2,y_2),\;X_3=(x_3,y_3),\;</math> drei Massen <math>m_1,m_2,m_3</math> platziert, so sind die Gleichgewichtsgleichungen für die Drehmomente um die Koordinatenachsen: |
|||
:'''(G)'''<math>\ \begin{array}{c} |
|||
Erfüllen die Koordinaten <math>(a_1,\ldots,a_n)</math> zusätzlich die ''Normierungsbedingung'' |
|||
(m_1+m_2+m_3)x_s = m_1x_1+m_2x_2 +m_3x_3\\ |
|||
(m_1+m_2+m_3)y_s = m_1y_1+m_2y_2 +m_3y_3 |
|||
\end{array}</math> |
|||
[[Datei:Baryzentr-ko-ebene.svg|mini|hochkant=1.8|Baryzentrische Koordinaten in der Ebene: In den Punkten <math>X_1,X_2,X_3</math> befinden sich die Massen <math>m_1,m_2,m_3</math>. Die lila farbigen parallelen Geraden haben die jeweils angegebenen Gleichungen. Ihr gemeinsamer Fernpunkt hat die Koordinaten <math>(1:-1:0)</math>]] |
|||
und der Schwerpunkt hat die Koordinaten |
|||
:'''(S)'''<math>\ \begin{array}{c} |
|||
x_s=\displaystyle \frac{m_1x_1+m_2x_2+m_3x_3}{m_1+m_2+m_3} \\ |
|||
y_s=\displaystyle \frac{m_1y_1+m_2y_2+m_3y_3}{m_1+m_2+m_3} |
|||
\end{array}</math> |
|||
=== Baryzentrische Koordinaten einer Ebene === |
|||
:<math>a_1 + \ldots + a_n = 1</math>, |
|||
Wie im 1-dimensionalen Fall kann man die Massen als (homogene) ''baryzentrische Koordinaten'' <math>(m_1:m_2:m_3) </math> von Punkten in der Ebene auffassen. |
|||
* Die ''Ecken'' des Dreiecks haben die homogenen Koordinaten |
|||
:<math>X_1=(1\!:\!0\!:\!0),\;X_2=(0\!:\!1\!:\!0),\;X_3=(0\!:\!0\!:\!1)\;</math>. |
|||
* Die Gerade durch die Punkte <math>X_1,X_2</math> wird durch die Gleichung <math>m_3=0</math> beschrieben und hat den ''Fernpunkt'' <math>(1:-1:0)</math>. ... |
|||
* Die ''Ferngerade'' ist durch die Gleichung <math>\;m_1+m_2+m_3=0\;</math> festgelegt. |
|||
* Eine beliebige ''Gerade'' wird durch eine Gleichung <math>\; am_1+bm_2+cm_3=0\;</math> beschrieben (s. homogene Koordinaten). |
|||
* Drei Geraden <math>\; a_1m_1+b_1m_2+c_1m_3=0,\; a_2m_1+b_2m_2+c_2m_3=0,\; a_3m_1+b_3m_2+c_3m_3=0\;\ </math> haben einen ''Punkt gemeinsam'', wenn |
|||
<math>\qquad\quad \left|\begin{matrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{matrix}\right| = 0</math>. |
|||
* Zwei Geraden <math>\; a_1m_1+b_1m_2+c_1m_3=0,\; a_2m_1+b_2m_2+c_2m_3=0</math> sind ''parallel'', wenn sie sich auf der Ferngerade schneiden, d.h., wenn |
|||
<math>\qquad \quad \left|\begin{matrix}a_1&b_1&c_1\\a_2&b_2&c_2\\1&1&1\end{matrix}\right| = 0</math>. |
|||
* Drei Punkte <math>(m_1:m_2:m_3)</math>, <math>(m'_1:m'_2:m'_3)</math> und <math>(m''_1:m''_2:m''_3)</math> liegen genau dann auf einer Geraden, wenn |
|||
<math>\qquad \quad\left|\begin{matrix}m_1&m_2&m_3\\m'_1&m'_2&m'_3\\m''_1&m''_2&m''_3\end{matrix}\right| = 0</math> |
|||
*Hieraus ergibt sich die Gleichung <math>\; am_1+bm_2+cm_3=0 \;</math> einer Gerade durch zwei vorgegebene Punkte <math>(u_1:v_1:w_1),(u_2:v_2:w_2)</math> in Determinantenform : |
|||
<math>\qquad \quad\left|\begin{matrix}m_1&m_2&m_3\\u_1&v_1&w_1\\u_2&v_2&w_2\end{matrix}\right| = 0</math> |
|||
* Baryzentrische Koordinaten eines Punktes <math>\color{red}(x_s,y_s)</math>, erhält man durch Auflösen der beiden Gleichgewichtsgleichungen '''(G)''' (unterbestimmtes lineares Gleichungssystem) nach <math>m_1,m_2,m_3</math>. Nimmt man die Normierungs-Gleichung |
|||
::'''(N)''' <math>\quad m_1+m_2+m_3=1\; </math> |
|||
hinzu, ist das LGS eindeutig und mit Hilfe der Cramerschen Regel lösbar. Es ergibt sich |
|||
'''(NB)''' |
|||
so spricht man von ''normierten baryzentrischen Koordinaten''. Diese sind eindeutig bestimmt. Normierte baryzentrische Koordinaten lassen sich einfach ermitteln, indem man jede einzelne Koordinate durch die Summe der Koordinaten dividiert. |
|||
<math>\qquad \begin{array}{l} |
|||
m_1=\displaystyle\frac{(y_2-y_3)({\color{red}x_s}-x_3)+(x_3-x_2)({\color{red}y_s}-y_3)}{(y_2-y_3)(x_1-x_3)+(x_3-x_2)(y_1-y_3)}\\ |
|||
m_2=\displaystyle\frac{(y_3-y_1)({\color{red}x_s}-x_3)+(x_1-x_3)({\color{red}y_s}-y_3)}{(y_2-y_3)(x_1-x_3)+(x_3-x_2)(y_1-y_3)}\\ |
|||
m_3=1-m_1-m_2 |
|||
\end{array}</math> |
|||
'''Spezialfall: Koordinatendreieck:''' |
|||
Hinweis: Die Begriffe werden nicht einheitlich verwendet. Viele Autoren sprechen nur dann von baryzentrischen Koordinaten, wenn die Normierungsbedingung erfüllt ist. |
|||
Für das spezielle rechtwinklige Dreieck <math>\;X_3=(0,0),X_1=(1,0),X_2=(0,1)\;</math> als Bezugsdreieck hat ein Punkt <math>(x,y)</math> die einfachen baryzentrischen Koordinaten <math>(x:y:1-x-y)</math>. |
|||
Falls die Koordinaten positiv sind, so liegt der Punkt <math>p</math> in der [[Konvexe Hülle|konvexen Hülle]] von <math>x_1,\ldots,x_n</math>, also dem Simplex mit diesen Eckpunkten. Die Darstellung eines Punktes innerhalb einer konvexen Hülle als Summe von Eckpunkten eines Simplex wird ''affine Kombination'' oder ''baryzentrische Kombination'' genannt. |
|||
=== Beziehung zu Dreiecksflächen und trilinearen Koordinaten === |
|||
Wie man aus der Umstellung |
|||
[[Datei:Baryzentr-ko-Flaeche.svg|mini|hochkant=1.5|Das Drehmoment um die Gerade durch <math>X_1,X_2</math> von <math>m_3</math> mit Hebel <math>h_3</math> ist gleich dem Moment der Gesamtmasse im Punkt <math>S </math> mit Hebel <math>d_3</math>, da die Hebel der Massen <math>m_1,m_2</math> bei dieser Drehung gleich 0 sind.]] |
|||
:<math>p = \frac{a_1 x_1 + \dotsb + a_n x_n}{a_1 + \dotsb + a_n}</math> |
|||
Setzt man die Drehmomente um die Dreiecksseiten der Gesamtmasse im Schwerpunkt <math>S</math> und der Einzelmassen gleich, ergeben sich die folgenden Gleichungen (s. Bild, i=1,2,3): |
|||
der Definitionsgleichung sieht, ist <math>p</math> der [[Massenmittelpunkt]] (das [[Baryzentrum]]) einer Anordnung von Massen <math>a_1,\ldots,a_n</math> an den Eckpunkten des Simplex <math>x_1,\ldots,x_n</math>. Dies ist der Ursprung des Begriffs ''baryzentrisch,'' der 1827 von [[August Ferdinand Möbius]] eingeführt wurde. |
|||
:'''(GS)''' <math>\ m_ih_i=(m_1+m_2+m_3)\; d_i\ .</math> |
|||
Dabei bedeuten <math>h_1,h_2,h_3</math> die drei Höhen des Dreiecks und <math>d_1,d_2,d_3</math> die Abstände des Schwerpunktes von den einzelnen Dreiecksseiten. Multipliziert man jede Gleichung mit der zugehörigen halben Dreiecksseite, entsteht links in jeder Gleichung als Faktor die Dreiecksfläche <math>\Delta</math> und rechts die Flächen <math>\Delta_i</math> der Teildreiecke (im Bild grün): |
|||
:'''(DF)''' <math>\ m_i\Delta=(m_1+m_2+m_3)\; \Delta_i\; .</math> |
|||
Hieraus erkennt man <ref>Felix Klein: ''Vorlesungen über höhere Geometrie'', Springer-Verlag, 1926, S. 13</ref> |
|||
:'''(BF)''' <math>\ (m_1:m_2:m_3)=(\Delta_1:\Delta_2:\Delta_3)\ </math> und |
|||
:'''(BT)''' <math> \ (m_1:m_2:m_3)=(\frac{d_1}{s_1}:\frac{d_2}{s_2}:\frac{d_3}{s_3})\ ,</math> |
|||
wobei <math>s_1=|X_2X_3|\; ...</math> die Längen der Dreiecksseiten sind. Damit auch negative Koordinaten (bei Punkten außerhalb des gegebenen Dreiecks) auftreten können, müssen die Dreieckflächen bzw. Abstände ''orientiert'' werden. |
|||
Die Beziehung '''(BT)''' zeigt den einfachen Zusammenhang der baryzentrischen Koordinaten mit den [[Trilineare Koordinaten|trilinearen Koordinaten]] <math>(d_1:d_2:d_3)</math> eines Punktes. Für ein [[gleichseitiges Dreieck]] sind die baryzentrischen und trilinearen Koordinaten gleich. |
|||
== Baryzentrische Koordinaten in der Dreiecksgeometrie == |
|||
[[Datei:TriangleBarycentricCoordinates.svg|mini|320px|Baryzentrische Koordinaten <math>(u,v,w)</math> eines gleichseitigen Dreiecks und eines rechtwinkligen Dreiecks.]] |
|||
=== Anwendung: Satz von Ceva === |
|||
In der [[Dreiecksgeometrie]] werden neben [[Trilineare Koordinaten|trilinearen Koordinaten]] häufig baryzentrische Koordinaten verwendet, um die Positionen [[Ausgezeichnete Punkte im Dreieck|ausgezeichneter Punkte]] in Bezug auf ein gegebenes Referenzdreieck <math>ABC</math> zu beschreiben. Neben der [[Tupel|Tripel]]-Schreibweise <math>(u,v,w)</math> ist auch die Notation <math>u:v:w</math> gebräuchlich. |
|||
[[Datei:Baryzentr-ko-ceva.svg|mini|hochkant=1.4|Satz von Ceva]] |
|||
;[[Satz von Ceva]] |
|||
Ist P ein Punkt innerhalb des Dreiecks <math>X_1,X_2,X_3</math> und <math>P_i</math> der Schnittpunkt der Gerade <math>\overline{PX_i}</math> mit der Seite <math>X_jX_k</math> (siehe Bild), so gilt |
|||
:<math>\frac{|X_2P_1|}{|X_3P_1|}\cdot\frac{|X_3P_2|}{|X_1P_2|}\cdot\frac{|X_1P_3|}{|X_2P_3|}=1\; .</math> |
|||
;Beweis |
|||
=== Berechnung === |
|||
Mit denPunkten in baryzentrischen Koordinaten: |
|||
:<math>( |
:<math>X_1=(1:0:0),\; X_2=(0:1:0),\; X_3=(0:0:1), \; </math> |
||
:<math>P=(\mu_1:\mu_2:\mu_3)</math> |
|||
Dabei bedeuten <math>\Delta_{BCP}</math>, <math>\Delta_{CAP}</math> und <math>\Delta_{ABP}</math> orientierte Dreiecksflächen, d. h., die Flächen der genannten Dreiecke erhalten bei positivem Umlaufsinn (Gegenuhrzeiger) ein positives [[Vorzeichen (Zahl)|Vorzeichen]], andernfalls ein negatives. |
|||
ergibt sich die Gleichung der Gerade (s. oben) <math>\overline{X_1P}</math> zu <math>\; \mu_3m_2-\mu_2m_3=0\;</math> und damit der Schnittpunkt mit der Gerade <math>\overline{X_2X_3}</math> (deren Gleichung <math>m_1=0</math> ist): <math>P_1=(0:\mu_2:\mu_3)</math>. Aus '''B1''' erhält man <math>|X_2P_1|:|X_3P_1|=\mu_3:\mu_2\; .</math> Führt man diese Überlegungen auch für die Geraden <math>\overline{X_3X_1},\overline{X_3X_1}</math> durch, ergibt sich |
|||
:<math>\frac{|X_2P_1|}{|X_3P_1|}\cdot\frac{|X_3P_2|}{|X_1P_2|}\cdot\frac{|X_1P_3|}{|X_2P_3|}=\frac{\mu_3}{\mu_2}\cdot \frac{\mu_1}{\mu_3}\cdot \frac{\mu_2}{\mu_1}= 1\; .</math> |
|||
== Allgemeine Definition baryzentrischer Koordinaten == |
|||
Eine explizite Formel, mit der sich aus den kartesischen Koordinaten der Ecken <math>A</math>, <math>B</math>, <math>C</math> und des Punktes <math>P</math> baryzentrische Koordinaten von <math>P</math> berechnen lassen, findet sich im Abschnitt Umrechnungsformeln. |
|||
Es seien <math>\mathbf{x}_1, \ldots, \mathbf{x}_n</math> die Ecken eines Simplex in einem [[Affine Räume|affinen Raum]] ''A''. Falls, für ein Punkt <math>\mathbf{p}</math> in ''A'', |
|||
=== Einfache Beispiele === |
|||
:<math> ( a_1 + \cdots + a_n ) \mathbf{p} = a_1 \, \mathbf{x}_1 + \cdots + a_n \, \mathbf{x}_n </math> |
|||
Die Ecken <math>A</math>, <math>B</math> und <math>C</math> des Referenzdreiecks haben die (normierten) baryzentrischen Koordinaten <math>(1,0,0)</math>, <math>(0,1,0)</math> beziehungsweise <math>(0,0,1)</math>. Der Schwerpunkt des Dreiecks <math>ABC</math> hat baryzentrische Koordinaten <math>(1,1,1)</math> beziehungsweise normiert <math>\left(\tfrac{1}{3}, \tfrac{1}{3}, \tfrac{1}{3}\right)</math>. |
|||
gilt und wenigstens eine der Zahlen <math>a_1, \ldots, a_n</math> nicht verschwindet, dann sagt man, die Koeffizienten <math>(a_1: \ldots: a_n</math>) sind die ''baryzentrischen Koordinaten''von <math>\mathbf{p}</math> bezüglich der Ecken <math>\mathbf{x}_1, \ldots, \mathbf{x}_n</math>. Die Ecken selbst haben die Koordinaten <math>\mathbf{x}_1=(1: 0: 0: \ldots: 0), \mathbf{x}_2=(0: 1: 0: \ldots: 0) \ldots, \mathbf{x}_n=(0: 0: 0: \ldots: 1)</math>. Baryzentrische Koordinaten sind nicht eindeutig: Für jedes ''c'' ungleich Null sind auch (<math>c a_1: \ldots: c a_n</math>) baryzentrische Koordinaten von <math>\mathbf{p}</math>. |
|||
=== Eigenschaften === |
|||
Erfüllen die Koordinaten <math>(a_1:\ldots:a_n)</math> zusätzlich die ''Normierungsbedingung'' |
|||
Drei Punkte mit baryzentrischen Koordinaten <math>(u_1,v_1,w_1)</math>, <math>(u_2,v_2,w_2)</math> und <math>(u_3,v_3,w_3)</math> liegen genau dann auf einer Geraden, wenn |
|||
:<math>a_1 + \ldots + a_n = 1</math>, |
|||
:<math>\left|\begin{matrix}u_1&v_1&w_1\\u_2&v_2&w_2\\u_3&v_3&w_3\end{matrix}\right| = 0</math> |
|||
so spricht man von ''normierten baryzentrischen Koordinaten''. Diese sind eindeutig bestimmt. Normierte baryzentrische Koordinaten lassen sich einfach ermitteln, indem man jede einzelne Koordinate durch die Summe der Koordinaten dividiert. |
|||
gilt. Diese Beziehung ermöglicht auch die Aufstellung von Geradengleichungen für baryzentrische Koordinaten. Solche Gleichungen haben die Form |
|||
Hinweis: Die Begriffe werden nicht einheitlich verwendet. Viele Autoren sprechen nur dann von baryzentrischen Koordinaten, wenn die Normierungsbedingung erfüllt ist. |
|||
:<math>\alpha u + \beta v + \gamma w = 0</math>, |
|||
Falls die Koordinaten positiv sind, so liegt der Punkt <math>\mathbf{p}</math> in der [[Konvexe Hülle|konvexen Hülle]] von <math>\mathbf{x}_1, \ldots, \mathbf{x}_n</math>, also dem Simplex mit diesen Eckpunkten. Die Darstellung eines Punktes innerhalb einer konvexen Hülle als Summe von Eckpunkten eines Simplex wird ''affine Kombination'' oder ''baryzentrische Kombination'' genannt. |
|||
wobei mindestens einer der reellen Koeffizienten <math>\alpha</math>, <math>\beta</math> und <math>\gamma</math> von 0 verschieden sein muss. |
|||
Wie man aus der Umstellung |
|||
Drei Geraden mit den baryzentrischen Gleichungen <math>\alpha_1 u + \beta_1 v + \gamma_1 w = 0</math>, <math>\alpha_2 u + \beta_2 v + \gamma_2 w = 0</math> und <math>\alpha_3 u + \beta_3 v + \gamma_3 w = 0</math> schneiden sich genau dann in einem Punkt oder sind parallel, wenn die Bedingung |
|||
:<math>\mathbf{p} = \frac{a_1 \mathbf{x}_1 + \dotsb + a_n \mathbf{x}_n}{a_1 + \dotsb + a_n}</math> |
|||
der Definitionsgleichung sieht, ist <math>\mathbf{p}</math> der [[Massenmittelpunkt]] (das [[Baryzentrum]]) einer Anordnung von Massen <math>a_1,\ldots,a_n</math> an den Eckpunkten des Simplex <math>\mathbf{x}_1,\ldots,\mathbf{x}_n</math>. Dies ist der Ursprung des Begriffs ''baryzentrisch''. |
|||
:<math>\left|\begin{matrix}\alpha_1&\beta_1&\gamma_1\\\alpha_2&\beta_2&\gamma_2\\\alpha_3&\beta_3&\gamma_3\end{matrix}\right| = 0</math> |
|||
erfüllt ist. |
|||
Die Parallelität zweier Geraden mit den Gleichungen <math>\alpha_1 u + \beta_1 v + \gamma_1 w = 0</math> und <math>\alpha_2 u + \beta_2 v + \gamma_2 w = 0</math> lässt sich überprüfen mit dem Kriterium |
|||
:<math>\left|\begin{matrix}\alpha_1&\beta_1&\gamma_1\\\alpha_2&\beta_2&\gamma_2\\1&1&1\end{matrix}\right| = 0</math>. |
|||
=== Umrechnungsformeln === |
|||
Zwischen [[Trilineare Koordinaten|trilinearen]] und baryzentrischen Koordinaten besteht ein einfacher Zusammenhang: Hat der gegebene Punkt die trilinearen Koordinaten <math>(r,s,t)</math>, so sind <math>(ar,bs,ct)</math> baryzentrische Koordinaten dieses Punktes. <math>a</math>, <math>b</math> und <math>c</math> bezeichnen dabei die Seitenlängen des Dreiecks. |
|||
Die Umrechnung in [[Kartesisches Koordinatensystem|kartesische Koordinaten]] erfolgt durch Bestimmung des gewichteten Mittels. Sind <math>(u,v,w)</math> baryzentrische Koordinaten eines Punktes <math>P(x,y)</math> und <math>(x_A,y_A)</math>, <math>(x_B,y_B)</math>, <math>(x_C,y_C)</math> die kartesischen Koordinaten der Ecken des gegebenen Dreiecks, so gilt: |
|||
:<math>x = \frac{u \cdot x_A + v \cdot x_B + w \cdot x_C}{u+v+w}</math> |
|||
:<math>y = \frac{u \cdot y_A + v \cdot y_B + w \cdot y_C}{u+v+w}</math> |
|||
Umgekehrt erhält man für einen in kartesischen Koordinaten gegebenen Punkt <math>P(x,y)</math> durch folgende Formeln |
|||
baryzentrische Koordinaten: |
|||
:<math>u=\frac{(y_B-y_C)(x-x_C)+(x_C-x_B)(y-y_C)}{(y_B-y_C)(x_A-x_C)+(x_C-x_B)(y_A-y_C)}\, ,</math> |
|||
:<math>v=\frac{(y_C-y_A)(x-x_C)+(x_A-x_C)(y-y_C)}{(y_B-y_C)(x_A-x_C)+(x_C-x_B)(y_A-y_C)}\, ,</math> |
|||
:<math>w=1-u-v.</math> |
|||
=== Anwendung zur Abstandsberechnung === |
|||
Der Abstand zweier Punkte <math>P</math> und <math>Q</math>, die durch normalisierte baryzentrische Koordinaten <math>(u_1,v_1,w_1)</math> und <math>(u_2,v_2,w_2)</math> festgelegt sind, lässt sich folgendermaßen berechnen:<ref>{{Literatur|Autor=Max Schindler, Evan Chen|Titel=Barycentric Coordinates in Olympiad Geometry|Datum=2012-07-13|Seiten=9-11|Online=https://web.evanchen.cc/handouts/bary/bary-full.pdf|Sprache=en}}</ref> Es wird der zugehörige Verschiebungsvektor |
|||
:<math>\overrightarrow{PQ} = (u_2-u_1, v_2-v_1, w_2-w_1)</math> |
|||
gebildet. Bezeichnet man die Koordinaten dieses Vektors mit <math>(x,y,z)</math>, so gilt für den Abstand der gegebenen Punkte: |
|||
:<math>|PQ|^2 = -a^2 y z - b^2 z x - c^2 x y</math> |
|||
== Verallgemeinerte baryzentrische Koordinaten == |
== Verallgemeinerte baryzentrische Koordinaten == |
||
Baryzentrische Koordinaten <math>(a_1,\ldots,a_n)</math>, die mit Bezug auf ein [[Polytop (Geometrie)|Polytop]] statt mit Bezug auf ein Simplex definiert sind, werden ''verallgemeinerte baryzentrische Koordinaten'' genannt. Hierbei wird weiterhin verlangt, dass die Gleichung |
Baryzentrische Koordinaten <math>(a_1,\ldots,a_n)</math>, die mit Bezug auf ein [[Polytop (Geometrie)|Polytop]] statt mit Bezug auf ein Simplex definiert sind, werden ''verallgemeinerte baryzentrische Koordinaten'' genannt. Hierbei wird weiterhin verlangt, dass die Gleichung |
||
:<math>(a_1 + \ |
:<math> ( a_1 + \cdots + a_n ) \mathbf{p} = a_1 \, \mathbf{x}_1 + \cdots + a_n \, \mathbf{x}_n </math> |
||
erfüllt wird, wobei <math> |
erfüllt wird, wobei <math>\mathbf{x}_1,\ldots,\mathbf{x}_n</math> hier die Eckpunkte des gegebenen Polytops sind. Die Definition ist also formal unverändert, allerdings muss ein Simplex mit <math>n</math> Eckpunkten in einem Vektorraum mit einer Dimension von mindestens <math>n-1</math> enthalten sein, während Polytope auch in Vektorräume von niedrigerer Dimension eingebettet sein können. Das einfachste Beispiel ist ein Viereck in der Ebene. Als Konsequenz sind sogar die normierten verallgemeinerten baryzentrischen Koordinaten für ein Polytop im Allgemeinen nicht eindeutig bestimmt, obwohl dies für normierte baryzentrische Koordinaten mit Bezug auf ein Simplex der Fall ist. |
||
Verallgemeinerte baryzentrische Koordinaten werden insbesondere in der [[Computergrafik]] bzw. der [[Geometrische Modellierung|geometrischen Modellierung]] verwendet. Dort können dreidimensionale Objekte oft durch Polyeder approximiert werden, sodass die verallgemeinerten baryzentrischen Koordinaten eine geometrische Bedeutung haben und die weitere Bearbeitung dieser Objekte erleichtern. |
Verallgemeinerte baryzentrische Koordinaten werden insbesondere in der [[Computergrafik]] bzw. der [[Geometrische Modellierung|geometrischen Modellierung]] verwendet. Dort können dreidimensionale Objekte oft durch Polyeder approximiert werden, sodass die verallgemeinerten baryzentrischen Koordinaten eine geometrische Bedeutung haben und die weitere Bearbeitung dieser Objekte erleichtern. |
||
| Zeile 127: | Zeile 158: | ||
== Literatur == |
== Literatur == |
||
* Oswin Aichholzer, Bert Jüttler: ''Einführung in die angewandte Geometrie.'' Springer-Verlag, Basel 2013, {{DOI|10.1007/978-3-0346-0651-6}}, ISBN 978-3-0346-0651-6, S. 59. |
|||
* Gerald Farin, Diane Hansford: ''Lineare Algebra: Ein geometrischer Zugang.'' Springer |
* Gerald Farin, Diane Hansford: ''Lineare Algebra: Ein geometrischer Zugang.'' Springer-Verlag, 2013, {{DOI|10.1007/978-3-642-55841-2}}, ISBN 978-3-540-41854-2, S. 139. |
||
* John Fauvel, Raymond Flood, Robin Wilson: ''Möbius und sein Band: Der Aufstieg von Mathematik und Astronomie im Deutschland des 19. Jahrhunderts.'' Springer-Verlag, 2013, ISBN 978-3-0348-6203-5, S. 106. |
|||
* Peter Knabner, Lutz Angermann: ''Numerik partieller Differentialgleichungen. Eine anwendungsorientierte Einführung.'' Springer 2000, ISBN 3642571816, S. 108–111 ({{Google Buch|BuchID=1xPc6-Ed4PgC|Seite=108|Linktext=Auszug (Google)|KeinText=ja}}). |
|||
* Peter Knabner, Lutz Angermann: ''Numerik partieller Differentialgleichungen. Eine anwendungsorientierte Einführung.'' Springer 2000, ISBN 3-642-57181-6, S. 108–111 ({{Google Buch|BuchID=1xPc6-Ed4PgC|Seite=108|Linktext=Auszug (Google)|KeinText=ja}}).<!-- so etwas bitte nicht das ist kein Auszug das ist ohne jeglichen Seitenzugriff -->([https://books.google.de/books?id=WdgjBgAAQBAJ&pg=PA108 books.google.de]). |
|||
* Abraham A. Ungar: ''Barycentric Calculus in Euclidean and Hyperbolic Geometry.'' World Scientific 2010, ISBN 9789814304931. |
|||
* Abraham A. Ungar: ''Barycentric Calculus in Euclidean and Hyperbolic Geometry.'' World Scientific 2010, ISBN 978-981-4304-93-1. |
|||
* John Vince: ''Mathematics for Computer Graphics.'' Springer 2010, ISBN 9781849960328, S. 208–236. |
|||
* John Vince: ''Mathematics for Computer Graphics.'' Springer 2010, ISBN 978-1-84996-032-8, S. 208–236. |
|||
== Weblinks == |
== Weblinks == |
||
* {{MathWorld|id=BarycentricCoordinates|title=Barycentric Coordinates}} |
* {{MathWorld|id=BarycentricCoordinates|title=Barycentric Coordinates}} |
||
* ''[https://www.encyclopediaofmath.org/index.php/Barycentric_coordinates Barycentric Coordinates.]'' Eintrag in der [[Encyclopaedia of Mathematics]]. |
* ''[https://www.encyclopediaofmath.org/index.php/Barycentric_coordinates Barycentric Coordinates.]'' Eintrag in der [[Encyclopaedia of Mathematics]]. |
||
Version vom 17. August 2020, 09:14 Uhr
 |
Dieser Artikel wurde auf der Qualitätssicherungsseite des Portals Mathematik eingetragen. Dies geschieht, um die Qualität der Artikel aus dem Themengebiet Mathematik auf ein akzeptables Niveau zu bringen.
Bitte hilf mit, die Mängel dieses Artikels zu beseitigen, und beteilige dich bitte an der Diskussion! (Artikel eintragen) |
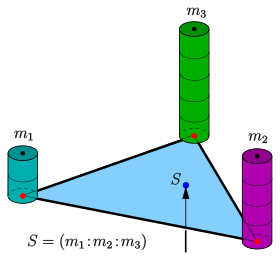
Sind alle Massen gleich, ist der Punkt der geometrische Schwerpunkt des Dreiecks und hat die Koordinaten
Baryzentrische Koordinaten (auch homogene baryzentrische Koordinaten) dienen in der linearen Algebra und in der Geometrie dazu, die Lage von Punkten in Bezug auf eine gegebene Strecke, ein gegebenes Dreieck, ein gegebenes Tetraeder oder allgemeiner ein gegebenes Simplex zu beschreiben.
Ebene baryzentrische Koordinaten eines Punktes kann man sich als Verhältnisse von drei Massen vorstellen, die sich in den Ecken eines vorgegeben Dreiecks befinden und deren Schwerpunkt ist (siehe Bild). Da es dabei nur auf Verhältnisse ankommt, schreibt man .
Baryzentrische Koordinaten wurden zuerst von A.F. Möbius 1827 in seinem Buch Der baryzentrische Calcul eingeführt.[1] Sie sind ein Spezialfall homogener Koordinaten. Ein wesentlicher Unterschied zu den üblichen homogenen Koordinaten, z. B. in der Ebene, ist die Beschreibung der Ferngerade durch die Gleichung statt durch .
Insbesondere in der Dreiecksgeometrie spielen die baryzentrischen Koordinaten, neben den trilinearen Koordinaten, eine wesentliche Rolle. Überall, wo es um Verhältnisse von Strecken geht, wie zum Beispiel in dem Satz von Ceva, sind sie ein hervorragendes Werkzeug. Aber nicht nur in der Geometrie, sondern auch im Bereich des Computer-aided Design verwendet man sie zur Erzeugung von dreieckigen Flächenstücken, den dreieckigen Bezierflächen. [2][3]
In dem Abschnitt Einführung baryzentrischer Koordinaten werden die Koordinaten mit bezeichnet, um immer wieder an ihre Beziehung zu Massen und deren Schwerpunkt zu erinnern, was oft eine Hilfe ist. Erst im Abschnitt Allgemeine baryzentrische Koordinaten werden die in der Mathematik üblichen Bezeichnungen benutzt.
Einführung baryzentrischer Koordinaten
2 Massen auf einer Gerade

Der Schwerpunkt zweier Massen , die auf der x-Achse an den Stellen platziert sind, ist der Punkt , an dem die Masse angebracht werden muss, so dass sie dasselbe Drehmoment bezüglich irgendeines Punktes bewirkt. Bezgl. des Nullpunktes muss also gelten [4].
- (G1) Auflösen ergibt
- (S1)
- Eigenschaften des Schwerpunkts
- Die Lage des Schwerpunkts hängt nicht von der zufälligen Wahl des Nullpunktes und einer Skalierung ab.
- Die Lage des Schwerpunktes hängt nur von dem Verhältnis ab. D.h.: Die Massen besitzen denselben Schwerpunkt.
- Lässt man negative Massen zu, z.B. , so ergibt sich für die Gesamtmasse und .
Baryzentrische Koordinaten einer Gerade

Die Beziehung eines Schwerpunktes zu zwei gegebenen Massen erlaubt es, einen beliebigen Punkt der x-Achse als Schwerpunkt zweier in platzierten Massen aufzufassen. Allerdings ist diese Zuordnung nicht eindeutig. Die Eindeutigkeit kann man aber mit der Forderung erzwingen.
Paare von Massen in den fest vorgegebenen Punkten kann man also als homogene Koordinaten eines Punktes (des Schwerpunktes der Massen) der x-Achse auffassen. Aufgrund dieser Beziehung, nennt man diese Koordinaten baryzentrische Koordinaten des Punktes . Der Punkt bzw. hat die homogenen Koordinaten bzw. . Für den Fernpunkt gilt . Er hat die baryzentrischen Koordinaten . Man beachte: Bei der üblichen (nicht baryzentrischen) homogenen Koordinatisierung wird der Fernpunkt durch (1:0) beschrieben !
Falls die Eindeutigkeit durch die Gleichung
- (N1)
erzwungen wird, spricht man von normierten baryzentrischen Koordinaten.
Ist ein Punkt gegeben, so erhält man seine baryzentrischen Koordinaten durch Auflösen der Gleichgewichtsgleichung (G1) nach , was als unterbestimmtes lineares Gleichungssystem nicht eindeutig möglich ist:

- (B1)
Dabei ist Dieser einfache Zusammenhang der baryzentrischen Koordinaten mit Verhältnissen von Strecken ist der Grund für ihre große Bedeutung in der Dreiecksgeometrie.
Im normierten Fall wird zur Gleichung (G1) die Normierungsgleichung (N1) hinzugenommen, wodurch das LGS für eindeutig wird. Lösung mit der Cramerschen Regel liefert
- und damit die normierten baryzentrischen Koordinaten
- (NB1)
Der Mittelpunkt der Punkte besitzt die baryzentrischen Koordinaten und in normierter Darstellung
3 Massen in einer Ebene
Sind in den Ecken eines Dreiecks drei Massen platziert, so sind die Gleichgewichtsgleichungen für die Drehmomente um die Koordinatenachsen:
- (G)

und der Schwerpunkt hat die Koordinaten
- (S)
Baryzentrische Koordinaten einer Ebene
Wie im 1-dimensionalen Fall kann man die Massen als (homogene) baryzentrische Koordinaten von Punkten in der Ebene auffassen.
- Die Ecken des Dreiecks haben die homogenen Koordinaten
- .
- Die Gerade durch die Punkte wird durch die Gleichung beschrieben und hat den Fernpunkt . ...
- Die Ferngerade ist durch die Gleichung festgelegt.
- Eine beliebige Gerade wird durch eine Gleichung beschrieben (s. homogene Koordinaten).
- Drei Geraden haben einen Punkt gemeinsam, wenn
.
- Zwei Geraden sind parallel, wenn sie sich auf der Ferngerade schneiden, d.h., wenn
.
- Drei Punkte , und liegen genau dann auf einer Geraden, wenn
- Hieraus ergibt sich die Gleichung einer Gerade durch zwei vorgegebene Punkte in Determinantenform :
- Baryzentrische Koordinaten eines Punktes , erhält man durch Auflösen der beiden Gleichgewichtsgleichungen (G) (unterbestimmtes lineares Gleichungssystem) nach . Nimmt man die Normierungs-Gleichung
- (N)
hinzu, ist das LGS eindeutig und mit Hilfe der Cramerschen Regel lösbar. Es ergibt sich
(NB)
Spezialfall: Koordinatendreieck:
Für das spezielle rechtwinklige Dreieck als Bezugsdreieck hat ein Punkt die einfachen baryzentrischen Koordinaten .
Beziehung zu Dreiecksflächen und trilinearen Koordinaten

Setzt man die Drehmomente um die Dreiecksseiten der Gesamtmasse im Schwerpunkt und der Einzelmassen gleich, ergeben sich die folgenden Gleichungen (s. Bild, i=1,2,3):
- (GS)
Dabei bedeuten die drei Höhen des Dreiecks und die Abstände des Schwerpunktes von den einzelnen Dreiecksseiten. Multipliziert man jede Gleichung mit der zugehörigen halben Dreiecksseite, entsteht links in jeder Gleichung als Faktor die Dreiecksfläche und rechts die Flächen der Teildreiecke (im Bild grün):
- (DF)
Hieraus erkennt man [5]
- (BF) und
- (BT)
wobei die Längen der Dreiecksseiten sind. Damit auch negative Koordinaten (bei Punkten außerhalb des gegebenen Dreiecks) auftreten können, müssen die Dreieckflächen bzw. Abstände orientiert werden.
Die Beziehung (BT) zeigt den einfachen Zusammenhang der baryzentrischen Koordinaten mit den trilinearen Koordinaten eines Punktes. Für ein gleichseitiges Dreieck sind die baryzentrischen und trilinearen Koordinaten gleich.
Anwendung: Satz von Ceva

Ist P ein Punkt innerhalb des Dreiecks und der Schnittpunkt der Gerade mit der Seite (siehe Bild), so gilt
- Beweis
Mit denPunkten in baryzentrischen Koordinaten:
ergibt sich die Gleichung der Gerade (s. oben) zu und damit der Schnittpunkt mit der Gerade (deren Gleichung ist): . Aus B1 erhält man Führt man diese Überlegungen auch für die Geraden durch, ergibt sich
Allgemeine Definition baryzentrischer Koordinaten
Es seien die Ecken eines Simplex in einem affinen Raum A. Falls, für ein Punkt in A,
gilt und wenigstens eine der Zahlen nicht verschwindet, dann sagt man, die Koeffizienten ) sind die baryzentrischen Koordinatenvon bezüglich der Ecken . Die Ecken selbst haben die Koordinaten . Baryzentrische Koordinaten sind nicht eindeutig: Für jedes c ungleich Null sind auch () baryzentrische Koordinaten von .
Erfüllen die Koordinaten zusätzlich die Normierungsbedingung
- ,
so spricht man von normierten baryzentrischen Koordinaten. Diese sind eindeutig bestimmt. Normierte baryzentrische Koordinaten lassen sich einfach ermitteln, indem man jede einzelne Koordinate durch die Summe der Koordinaten dividiert.
Hinweis: Die Begriffe werden nicht einheitlich verwendet. Viele Autoren sprechen nur dann von baryzentrischen Koordinaten, wenn die Normierungsbedingung erfüllt ist.
Falls die Koordinaten positiv sind, so liegt der Punkt in der konvexen Hülle von , also dem Simplex mit diesen Eckpunkten. Die Darstellung eines Punktes innerhalb einer konvexen Hülle als Summe von Eckpunkten eines Simplex wird affine Kombination oder baryzentrische Kombination genannt.
Wie man aus der Umstellung
der Definitionsgleichung sieht, ist der Massenmittelpunkt (das Baryzentrum) einer Anordnung von Massen an den Eckpunkten des Simplex . Dies ist der Ursprung des Begriffs baryzentrisch.
Verallgemeinerte baryzentrische Koordinaten
Baryzentrische Koordinaten , die mit Bezug auf ein Polytop statt mit Bezug auf ein Simplex definiert sind, werden verallgemeinerte baryzentrische Koordinaten genannt. Hierbei wird weiterhin verlangt, dass die Gleichung
erfüllt wird, wobei hier die Eckpunkte des gegebenen Polytops sind. Die Definition ist also formal unverändert, allerdings muss ein Simplex mit Eckpunkten in einem Vektorraum mit einer Dimension von mindestens enthalten sein, während Polytope auch in Vektorräume von niedrigerer Dimension eingebettet sein können. Das einfachste Beispiel ist ein Viereck in der Ebene. Als Konsequenz sind sogar die normierten verallgemeinerten baryzentrischen Koordinaten für ein Polytop im Allgemeinen nicht eindeutig bestimmt, obwohl dies für normierte baryzentrische Koordinaten mit Bezug auf ein Simplex der Fall ist.
Verallgemeinerte baryzentrische Koordinaten werden insbesondere in der Computergrafik bzw. der geometrischen Modellierung verwendet. Dort können dreidimensionale Objekte oft durch Polyeder approximiert werden, sodass die verallgemeinerten baryzentrischen Koordinaten eine geometrische Bedeutung haben und die weitere Bearbeitung dieser Objekte erleichtern.
Baryzentrische Interpolation
Auf baryzentrischen Koordinaten basiert ein Interpolationsverfahren, das die lineare Interpolation für Funktionen mehrerer Variablen verallgemeinert.
Im Falle einer Funktion von zwei Variablen und sind für drei Punkte , und die Funktionswerte gegeben. Dabei dürfen , und nicht auf einer Geraden liegen. Sie müssen also ein Dreieck aufspannen. Ist nun ein beliebiger Punkt gegeben, so definiert man
- ,
wobei die normierten baryzentrischen Koordinaten von sind. Diese Interpolation funktioniert auch für Punkte außerhalb des Dreiecks.
Literatur
- Oswin Aichholzer, Bert Jüttler: Einführung in die angewandte Geometrie. Springer-Verlag, Basel 2013, doi:10.1007/978-3-0346-0651-6, ISBN 978-3-0346-0651-6, S. 59.
- Gerald Farin, Diane Hansford: Lineare Algebra: Ein geometrischer Zugang. Springer-Verlag, 2013, doi:10.1007/978-3-642-55841-2, ISBN 978-3-540-41854-2, S. 139.
- John Fauvel, Raymond Flood, Robin Wilson: Möbius und sein Band: Der Aufstieg von Mathematik und Astronomie im Deutschland des 19. Jahrhunderts. Springer-Verlag, 2013, ISBN 978-3-0348-6203-5, S. 106.
- Peter Knabner, Lutz Angermann: Numerik partieller Differentialgleichungen. Eine anwendungsorientierte Einführung. Springer 2000, ISBN 3-642-57181-6, S. 108–111 (Auszug (Google)).(books.google.de).
- Abraham A. Ungar: Barycentric Calculus in Euclidean and Hyperbolic Geometry. World Scientific 2010, ISBN 978-981-4304-93-1.
- John Vince: Mathematics for Computer Graphics. Springer 2010, ISBN 978-1-84996-032-8, S. 208–236.
Weblinks
- Eric W. Weisstein: Barycentric Coordinates. In: MathWorld (englisch).
- Barycentric Coordinates. Eintrag in der Encyclopaedia of Mathematics.
- Barycentric Coordinates. Eintrag auf PlanetMath.
- Philipp B. Laval: Mathematics for Computer Graphics – Barycentric Coordinates. (PDF; 137 kB).
Einzelnachweise
- ↑ Max Koecher, Aloys Krieg: Ebene Geometrie. Springer-Verlag, Berlin 2007, ISBN 978-3-540-49328-0, S. 76.
- ↑ Josef Hoschek, Dieter Lasser: Grundlagen der geometriechen Datenverarbeitung. Teubner-Verlag,, 1989, ISBN 3-519-02962-6, S. 243.
- ↑ Gerald Farin: Curves and Surfeces for Computer Aided Geometric Design. Academic Press, 1990, ISBN 0-12-249051-7, S. 20.
- ↑ Christian Gerthsen: Physik, Springer-Verlag, 1963, S. 37
- ↑ Felix Klein: Vorlesungen über höhere Geometrie, Springer-Verlag, 1926, S. 13


















































































































