Beschränktes Wachstum
Als beschränktes Wachstum (begrenztes Wachstum) wird in der Mathematik ein Wachstum bezeichnet, das durch eine natürliche Schranke (auch Kapazität(-sgrenze) oder Sättigung(-sgrenze/-swert) genannt) begrenzt ist. Das Wachstum kann sowohl nach oben als auch nach unten (beschränkte Schrumpfung) beschränkt sein.
Eigenschaften[Bearbeiten | Quelltext bearbeiten]
Modellbeschreibung[Bearbeiten | Quelltext bearbeiten]
Beim klassischen Wachstumsmodell des beschränkten Wachstums ist die Änderungsrate bzw. proportional zum Sättigungsmanko (auch Restbestand bzw. Sättigungsdefizit genannt). Das Sättigungsmanko selbst nimmt exponentiell ab. Dieser Rest gibt den Fehlbetrag bis zum Erreichen der Schranke an. Der Bestand ergibt sich wiederum aus der Differenz von Sättigungsgrenze und Sättigungsmanko.
Wesentliche Begriffe und Notation[Bearbeiten | Quelltext bearbeiten]
- bezeichnet die Zeit.
- sei die betrachtete Bestandsgröße.
- kennzeichnet den Anfangsbestand (Anfangsbedingung) zum Zeitpunkt .
- bezeichnet die natürliche Schranke, die als Grenzwert von der Bestandsgröße (theoretisch) nicht überschritten werden kann. Sie bildet die Asymptote der Wachstumsfunktion und verhindert, dass der Bestand ins Unendliche wächst wie bei linearem und exponentiellen Wachstum.
- sei die Wachstumskonstante.
- gibt die Wachstumsgeschwindigkeit bzw. die Wachstumsrate an.
Differentialgleichung[Bearbeiten | Quelltext bearbeiten]
Differentialgleichungen (DGL) dienen der Beschreibung des kontinuierlichen (stetigen) Wachstumsmodells.
Die DGL für beschränktes Wachstum lautet:
Dies ist eine lineare inhomogene Differentialgleichung mit konstanten Koeffizienten und kann mittels der Methode „Variablentrennung“ gelöst werden.

Explizite Darstellung (Wachstumsfunktion)[Bearbeiten | Quelltext bearbeiten]
Die spezielle Lösung der DGL bildet die explizite Darstellung und damit gleichzeitig die Wachstumsfunktion.
Für ein beschränktes Wachstum lautet die Funktionsgleichung: Das Wachstum ist degressiv. Die Wachstumsgeschwindigkeit nimmt mit der Zeit ab.
Für ein nach oben beschränktes Wachstum mit steigt der Graph der Funktion streng monoton und beschreibt eine Rechtskurve.
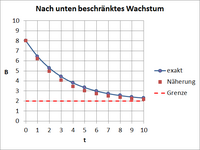
Für ein nach unten beschränktes Wachstum mit fällt der Graph der Funktion streng monoton und beschreibt eine Linkskurve.
Für den Sonderfall hat die Wachstumsfunktion die Gestalt: .
Hier fällt die Schranke mit der x-Achse (Abszisse) zusammen. Dies entspricht dem klassischen Fall einer exponentiellen Abnahme.
Rekursive Darstellung[Bearbeiten | Quelltext bearbeiten]
Zur Beschreibung des diskreten Modells als rekursive Darstellung dienen aus Differenzen abgeleitete Folgen.
Exakte Diskretisierung[Bearbeiten | Quelltext bearbeiten]
Es sei .
Dann lautet die Rekursionsformel: ,
wobei eine äquidistante Folge von Zeitpunkten darstellt und die entsprechenden Bestandsgrößen meint.
Genäherte Diskretisierung[Bearbeiten | Quelltext bearbeiten]
Folgende Näherung ergibt sich durch Anwendung des expliziten Eulerverfahrens:
mit
Vergleich zwischen der exakten und der genäherten Darstellung[Bearbeiten | Quelltext bearbeiten]
Der Koeffizientenvergleich der exakten und der Näherungsformeln zeigt, dass beide Darstellungen nicht identisch sind. Durch Reihenentwicklung der Exponentialfunktion:
ergibt sich jedoch, dass beide Darstellungen bis auf Terme höherer als 1. Ordnung übereinstimmen.
Beschränktes logistisches Wachstum[Bearbeiten | Quelltext bearbeiten]
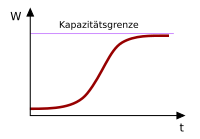
Neben dem klassischen Modell ist ein Wachstum, welches sich durch eine logistische Funktion beschreiben lässt, ebenfalls nach oben hin beschränkt. Hier ist die Änderungsrate proportional zum Produkt aus Bestand und Sättigungsmanko .
Beispiele[Bearbeiten | Quelltext bearbeiten]
Nach oben beschränktes Wachstum[Bearbeiten | Quelltext bearbeiten]
- Erwärmung eines Kaltgetränks
- Liegt die Temperatur eines Kaltgetränks unterhalb der Umgebungstemperatur, erwärmt sich das Getränk bis auf die Umgebungstemperatur, welche die obere Grenze bildet.
- Verkauf von Telefonanschlüssen an einem festen Ort
- Wenn alle Einwohner des Ortes einen Telefonanschluss besitzen, ist die obere Grenze erreicht.
- Medikamenteneinnahme
- Zu Beginn der Einnahme baut sich ein Wirkstoffniveau auf, das bei kontinuierlicher Medikamentation die obere Grenze beschreibt.
- Ausbreitung einer Population in einem begrenzten Raum
- Eine Population z. B. Fische wächst nicht immer weiter, sondern aufgrund von begrenzten Ressourcen wie Futter, Sauerstoff, Platz etc. existiert eine natürliche Grenze.
Nach unten beschränktes Wachstum[Bearbeiten | Quelltext bearbeiten]
- Abkühlung eines Heißgetränks
- Liegt die Temperatur eines Heißgetränks oberhalb der Umgebungstemperatur, kühlt sich das Getränk bis auf die Umgebungstemperatur ab, welche die untere Grenze bildet.
Literatur[Bearbeiten | Quelltext bearbeiten]
- Joachim Engel: Anwendungsorientierte Mathematik: Von Daten zur Funktion. S. 152–154, Springer Verlag, Heidelberg 2010, ISBN 978-3-540-89086-7.
- Hermann Haarmann, Hans Wolpers: Mathematik zur Erlangung der allgemeinen Hochschulreife, Nichttechnische Fachrichtungen. S. 273–274, 2. Auflage. Merkur Verlag, Rinteln 2012, ISBN 978-3-8120-0062-8.
- Harro Heuser: Gewöhnliche Differentialgleichungen: Einführung in Lehre und Gebrauch. S. 25–27, 70–72, Teubner Verlag, Wiesbaden, 5. Auflage 2006, ISBN 978-3-519-42227-3.
- Klaus Schilling: Analysis: Qualifikationsphase. S. 207–218, EINS Verlag, Köln 2012, ISBN 978-3-427-06660-6.
- Walter Seifritz: Wachstum, Rückkopplung und Chaos: Eine Einführung in die Welt der Nichtlinearität und des Chaos. Hanser Verlag, München 1987, ISBN 3-446-15105-2.
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Zum Wiki: Beschränktes Wachstum
- Aufgabenbeispiele mit Lösungen (Abituraufgaben Baden-Württemberg) ( vom 23. Dezember 2012 im Internet Archive)

























