Helix

R: rechtsgängige Helix
Die Gängigkeit der Helix ist absolut, d. h., sie ist unabhängig davon, ob man entlang der Achse von oben oder von unten auf die Helix blickt.
Die Helix (von griechisch ἕλιξ hélix „Windung, Kreislauf“; Plural Helices oder Helizes), auch Schraube, Schraubenlinie, zylindrische Spirale oder Wendel genannt, ist eine Kurve, die sich mit konstanter Steigung um den Mantel eines Zylinders windet.
Windungsrichtung[Bearbeiten | Quelltext bearbeiten]
Zur Benennung der Windungsrichtung (Helizität): man schaut entlang ihrer Achse längs durch die Helix; wenn sie sich beim Entfernen vom Betrachter im Uhrzeigersinn windet, ist sie rechtsgängig, andernfalls linksgängig.
Die Benennung folgt auch der Rechte-Faust-Regel, weshalb kontextabhängig ebenfalls von Händigkeit (engl. right-handed oder left-handed) gesprochen wird.
In der Botanik werden Pflanzen von oben, d. h. entgegen der Wuchsrichtung betrachtet. Anders als in der obigen allgemeinen Definition kommt das Betrachtungsobjekt also auf den Betrachter zu. Daher werden z. B. als rechtsgängige Helix wachsende Pflanzen linkswindend genannt, weil sie sich von oben betrachtet gegen den Uhrzeigersinn drehen.


Mathematische Beschreibung[Bearbeiten | Quelltext bearbeiten]
Die vektorielle Beschreibung einer Schraubenlinie in kartesischen Koordinaten lautet:
- Dabei ist die Anzahl der von aus durchlaufenen Windungen.
- Dabei ist die Ganghöhe, also diejenige Strecke, um die sich die Schraube bei einer vollen Umdrehung nach oben (in Richtung der Zylinderachse; z-Richtung) windet, der Radius und die Verschiebung der Schraube in z-Richtung.
- ist die Steigung der Helix: Die Helix wird zu einer Geraden mit Steigung , wenn man den Zylindermantel mit der Helix in die Ebene abwickelt.
- Man nennt den Gangwinkel der Helix.
Ganghöhe und Gangwinkel sind zwei in den technischen Anwendungen der Helix grundlegende Kenngrößen, etwa für die Normung von Gewinden.
- Eigenschaften
- Für linksgängige Helices wird negativ.
- Die Bogenlänge der Helix berechnet sich zu:
- Konstant sind die Krümmung , der Krümmungsradius (der zweite Summand ist der Krümmungsdefekt in Bezug zum umwickelten Zylinder) und die Windung .
- Die Torsion bezeichnet das Maß dafür, wie stark ein Draht in sich verwunden wird, wenn man daraus eine Helix windet.
Die Helix ist eine chirale Kurve, weil sie selbst mit ihrem Spiegelbild nicht durch Drehen und Verschieben zur Deckung gebracht werden kann. So ergibt die Spiegelung einer Schraube mit Rechtsgewinde eine Schraube mit Linksgewinde. Und beide sind nicht deckungsgleich, weder im dreidimensionalen Raum, noch als zweidimensionales Abbild.
Mehrgängige Schrauben[Bearbeiten | Quelltext bearbeiten]
Setzt man zwei kongruente Helices um eine halbe Ganghöhe versetzt zusammen (), ergibt sich eine zweigängige Schraube. Das gleiche Ergebnis erhält man, wenn man die zweite Helix um eine halbe Umdrehung versetzt. Die beiden Helices haben dann konstanten Abstand und berühren sich nie, die entstehende Kurve zerfällt also in zwei Äste. Analoge Bildung mit mehreren Helices ergibt entsprechend mehrgängige Schraubenlinien. Diese Definitionen spielen in der Technik eine wichtige Rolle.
Helix und Spirale[Bearbeiten | Quelltext bearbeiten]
Bei der Zentralprojektion einer Helix in Richtung der Achse auf eine ebene Fläche entsteht eine hyperbolische Spirale, bei der sich also der Radius der Windungen stetig verkleinert, so dass sie in der Ebene ineinander liegen. Das entspricht dem Blick in eine Helix entlang der Achse (siehe Abbildung der Doppel-Wendeltreppe), weil das Auge die Zentralperspektive sieht.
Beispiele für Helix-Formen in Natur und Technik[Bearbeiten | Quelltext bearbeiten]
Helices in Natur und Technik
- dienen Pflanzenranken der Verankerung,
- bieten eine Platzersparnis durch die „Aufwicklung“ der Geraden zu einem Zylinder (zum Beispiel bei Schraubenfedern oder Telefon- und Verlängerungskabeln),
- lassen sich als kompakter mechanischer Kraftwandler einsetzen, wie es beim Gewinde von Schrauben ausgenutzt wird.
Schraubenförmige Strukturen[Bearbeiten | Quelltext bearbeiten]
-
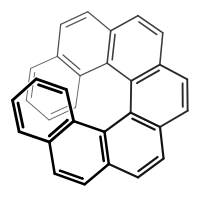
Chemie: Die molekulare Helix in (M)-(−)-Heptahelicen weist Helizität wie ein Linksgewinde auf.
-
Doppel-Wendeltreppe in den Vatikanischen Museen in Rom. Der Baukörper ist zweigängig schraubenförmig – ein Treppengang kann als Aufgang, der andere als Abgang genutzt werden, ermöglicht guten Personenverkehr in einem Museum. Die Chiralität der Doppelhelix entspricht einem Rechtsgewinde.
-
Die Schraubendrehung dieser Ranke entspricht oben zunächst dem Drehsinn einer Linksschraube und wechselt dreimal den Drehsinn. Die gewachsene Form weicht in Abschnitten kaum, in anderen deutlich von der idealen Helix ab.
Das bekannteste schraubig aufgebaute Biopolymer ist die DNA, die wegen der zwei umeinanderlaufenden, komplementären DNA-Einzelstränge auch als Doppelhelix bezeichnet wird. Ferner sind Teilabschnitte vieler Proteine, vor allem auch solcher, die in Biomembranen integriert sind (integrale Proteine), helikal aufgebaut. Diesen Strukturtyp der Sekundärstruktur bezeichnet man als α-Helix. Auch das pro Windung aus etwa 6 α-D-Glucoseeinheiten aufgebaute Polysaccharid Amylose, das neben Amylopektin in Stärke enthalten ist, hat die Form einer Helix.
In der Chemie gibt es Kohlenwasserstoffe – die Helicene – mit schraubenartigem Aufbau.[1]
In der Technik ist eine Wendel ein oft freitragendes schraubenförmiges Draht-Bauteil (Glühwendel, Wendelantenne, Drahtwiderstand, Wendelrohrpatrone). Eine weitere typische Helix ist die Schraubenfeder, bei der eine lange (und damit weiche) Torsionsfeder auf geringen Raum unterzubringen ist. Auch die Wendeltreppe spart Platz, weil nur geringe Grundfläche beansprucht wird. Gleiches gilt für die wendelförmigen Rampen etwa in Tiefgaragen und Parkhäusern. Der Draht einer Glühlampe ist häufig eine Doppelwendel, also eine Helix, um die eine weitere Helix verläuft (Aufbau siehe Bildbeispiele). Andere Beispiele sind der äußere Rand der Ohrmuschel oder die Peptidketten aus Kollagen.
Gewendelte Rutschen für Personen, etwa im Aussichtsturm Pyramidenkogel haben den Vorzug bei Erhöhung der Geschwindigkeit durch die Fliehkraft die Anpresskraft zu erhöhen. Ähnlich geformte Rutschen für Briefe und Pakete werden auch Sortierschnecken genannt.[2]
Mischdüsen für 2-Komponenten-Kleber (oder -Kitt) haben häufig zylindrische bis konische Helix-Einsätze.
Die Doppel-Wendeltreppe in der Grazer Burg besteht aus zwei einander durchdringenden Wendeltreppen, deren Schraubensinne gegenläufig sind und deren Achsen nebeneinander hochstreben.
In Jausenverkaufsautomaten, die hinter einem Glasfenster sichtbar mit Zuckerlsackerl, Schokoriegel etc. bestückt sind, transportieren Wendel aus dickem verchromtem Stahldraht mit einer Umdrehung jeweils einen angeforderten Artikel nach vorne zum Fall in den Auswurf. Je Gewindegang steckt ein Artikel schräg in der Schraube, alle nachfolgenden werden dabei längs der Lagerrille einen Schritt weit nach vorne geschoben.
Schraube und Keilwirkung[Bearbeiten | Quelltext bearbeiten]
Die Keilwirkung beruht darauf, dass der Steigungswinkel eine Bewegung entlang der langen Kathete in eine Normalbewegung entlang der kurzen Kathete „übersetzt“ (eine schiefe Ebene entlang eines Zylinders als einfache Maschine). Aufgrund des Hebelgesetzes ist dann die entstehende Normalkraft um das Verhältnis der Katheten größer als die eingesetzte Kraft. Je kleiner der Steigungswinkel (je flacher der Keil), desto stärker die Wirkung.
Das gilt für die Helix analog. Daher kann ein relativ kleines Drehmoment um die Mittelachse (kleine Tangentialkraft) in eine große Kraft entlang der Achse umgesetzt werden. Auf diesem Prinzip beruht das Gewinde einer Schraube mit Mutter ebenso wie das der archimedischen Schraube und des Schneckenförderers. Die Funktionsweise des Propellers oder der Gewindespindel im Maschinenbau beruht auf Umwandlung von Umdrehung in Vortrieb/Vorschub. Die Justierschraube nutzt im Umkehrschluss die Reduzierung des Weges, was eine feine Einstellung möglich macht. Auch Korkenzieher mit und ohne „Seele“ sind wendelförmig.
Die Spannuten von Bohrern sind wendelförmig um den Bohrermantel angeordnet. Umgangssprachlich werden die Bohrer fälschlicherweise Spiralbohrer genannt.
Doppelte Keilwirkung entsteht durch konische Schrauben: Nagelbohrer für Weichholz, die bis um 1975 üblichen Holzschrauben, heute noch die Maschinschrauben mit Sechskantkopf. Nur Gewindeausdreher haben ein Linksgewinde.
Seilerei[Bearbeiten | Quelltext bearbeiten]
Eine weitere Anwendung ist die Seilerei. Während die Bruchlast für einen einzelnen Faden oder ein paralleles Faserbündel nur vom Querschnitt abhängig ist, und daher auch Dicke und Schwere stark zunehmen, sind bei einem Seil die einzelnen Fasern oder Litzen verdrillt („geschlagen“). Bei Belastung erzeugt die Zugkraft eine zur Faser normale Kraft, die – weil die Steigung der Helices nahe bei 90° liegt und die Keilwirkung sich umkehrt – pro Länge eines Durchmessers deutlich geringer ist. Zusätzlich wird sie als Druckspannung auf die Nachbarfasern und/oder die Seele übertragen. Dabei heben sich die Kräfte zwischen den einzelnen Fasern oder Litzen auf, die Seele wird extrem komprimiert (daher werden dafür elastische Materialien verwendet) und nimmt die Energie auf.
Ausschließlich durch Schlag eine Richtung hergestellte Seile reagieren auf Zugbelastung durch ein Drehmoment zwischen den Enden und erlaubt man diesen Drehung durch Entdrillen. Begegnet wird diesem in der Regel unerwünschten Effekt durch Einbau axial verdrehbarer Wirbel – etwa zwischen Einzelseil und Kranhaken, in Abspannseilen z. B. von Oberleitungen, an Bowdenzügen, Personenliftkabinen oder mulfiler Angelleine. Entdrillen oder Drallmoment wird auch erzeugt, wenn ein Seil unter Zug über eine Kante oder Seilrolle läuft oder ein Nähzwirn durch ein Nadelöhr gezogen wird. Um diese Erscheinungen so weit wie möglich zu vermeiden, wird ein Seil (oder Kabel) in beide Richtungen geschlagen: So können die Litzen (in sich) in eine Richtung geschlagen sein, die Litzen zum Seil jedoch in die andere Richtung. Oder Lagen von Litzen können in wechselnder Schlagrichtung verseilt werden. Drallfreie Seile sind das Ziel, etwa auch um Seilbahnen sicher über Tragrollen zu führen.
Erst das Schlagen eines Seils ergibt seinen Zusammenhalt über den kreisförmigen Querschnitt und verschmerzt das stellenweise Versagen von einzelnen Litzen. Mit stärkerem Schlag erzeugte Seile sind auf Zugbelastung weicher.
In geflochtenen Seilen werden links und rechts verdrillt laufende Faserbündel miteinander verflochten (rund verwebt). Sowohl Kern-Mantel-Seile, ebenso konstruierte flache textile Hebeschlingen und viele Schnürsenkel weisen im Kern unverdrillt liegende Faserbündel auf, die prinzipiell keinen Drall erzeugen können.
Es gibt Kabel zur Datenübertragung die entlang ihrer Länge (!) mit wechselnder Schlagrichtung erzeugt werden. An den (markierten) Umkehrpunkten ist es möglich, eine Litze beiderseits ein Stück herauszulösen, um sie entspannt mit etwas Mehrlänge zur Bearbeitung etwas abseits des Kabels frei liegen zu haben.
Rohre und Schläuche[Bearbeiten | Quelltext bearbeiten]
Aus dünnem verzinktem Stahlblech werden durch Wendeln und Verbördeln Lüftungsrohre von typisch 20–60 cm Durchmesser gefertigt.[3] Dickwandige Stahlrohre für Pipelines, Fernwärme, als Kraftwerksdruckrohre von 30 bis 400 cm Durchmesser werden durch Biegen von Blech zum Wendel und Verschweissen auf Stoß hergestellt.[4]
Schutzschlauch zur Badewannenhandbrause, für elektrische Kabel zu Schwenktüren und -fenstern, auch Schwanenhals werden aus gewendeltem Metallblechstreifen mit S-förmigem Profil erzeugt. Die Verschieblichkeit zwischen zwei benachbarten Gängen der Wendel bewirkt die große Krümmbarkeit der Schlauchachse oder auch Dehnbarkeit in Richtung dieser Achse. Es gibt Rohrmaterial aus mehrfach gefalzter Alufolie mit um 10 cm Durchmesser für kleinere Entlüftungen in Wohnungen, das nur einmalig biegbar und streckbar sind. (Faltenbälge – Gelenke an Fernwärmeleitungen, Vakuumtechnik – sind dünnwandige Rohre die mit Rillen ohne Wendelung biegsam und dehnbar gefertigt wurden.)
Zylindrische Kartonhülsen als Wickelkern für Toilettenpapier und Auslegeware, Schalung für Betonsäulen oder für Feuerwerkskörper werden durch endloses wendelndes Wickeln erzeugt.
Dichte Kunststoffschläuche für Staubsauger werden durch Rillen im Mantel biegsam. Zumeist liegt eine gewendelte Rille vor, womit sich die Einschraubbarkeit in Anschlussstücke ergibt und die Möglichkeit zum Einbau eines Drahtwendels um den Unterdruck führenden Schlauch im Lumen zu stabilisieren. (Rillenschlauch der Elektroinstallation ist in der Regel nicht gewendelt.)
Staubabsaugungen an größeren Maschinen, Saugschläuche der Kanalreinigung und der Feuerwehr verwenden typisch Schläuche mit innenliegendem Drahtwendel, eventuell mit zwischen seinen Gängen außen liegender Einschnürung durch ein Seilchen.
Physik[Bearbeiten | Quelltext bearbeiten]
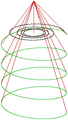
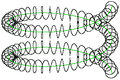
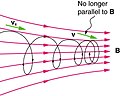
In der Physik vollführt ein elektrisch geladenes Teilchen, das sich in einem Magnetfeld bewegt, eine schraubenförmige Flugbahn. Voraussetzung ist, dass sich das Teilchen nicht parallel, antiparallel oder quer zur Nord-Süd-Ausrichtung des Magnetfeldes bewegt. Die Kraft, die das Teilchen auf diese schraubenförmige Flugbahn zwingt, heißt Lorentzkraft. Bei der Bewegung parallel oder antiparallel zur Nord-Süd-Ausrichtung des Magnetfeldes entsteht eine gerade Flugbahn und bei der Bewegung quer zur Nord-Süd-Ausrichtung des Magnetfeldes entsteht eine Kreisbahn. Wenn ein elektrisch geladenes Teilchen auf einer solchen Kreisbahn Energie durch elektromagnetische Strahlung abgibt, dann bewegt es sich auf einer immer enger werdenden Spiralbahn. Die schraubenförmige Flugbahn des elektrisch geladenen Teilchens ist eine Überlagerung einer geraden Flugbahn, und einer Kreisbahn. Bei Energieverlusten durch elektromagnetische Strahlung, und auch in inhomogenen Magnetfeldern, entstehen konische Spiralen aus der Überlagerung von Schraube und Spirale.
Bahnen[Bearbeiten | Quelltext bearbeiten]
Die Figur der Schraube – Drehung um die Körperlängsachse – beim Wasser- und Fallschirmspringen oder bei Sprungakrobatik bewirkt, dass sich außenliegende Körperpunkte entlang einer Helix bewegen, die noch entlang einer Wurfparabel gekrümmt sein kann.
Die entsprechende Figur im Kunstflug nennt sich Rolle.
Jeder Punkt auf einem zur Stabilisierung mit Drall fliegenden Geschoss erzeugt eine Helix. Rotieren Sportbogen- und eventuell Dartpfeil, so beschreibt jedes Flügelende eine Helix. Einfache Raketen können insbesondere in der Antriebsphase durch Drall um die Längsachse stabilisiert werden. Umläuft ein mit Eigenrotation ausgerichteter Satellit die Erde, erzeugt ein Punkt auf seinem Mantel nur dann recht genau eine Helix, wenn und solange die momentane Flugrichtung in Richtung des Rotationsvektors weist.
Bildbeispiele[Bearbeiten | Quelltext bearbeiten]
-
Wendelkabel (z. B. am Telefonapparat)
-
Helix, leicht perspektivisch
-
Helix (grün) und hyperbolische Spirale (schwarz)
-
Schraube entlang einer Schraube, Doppelwendel (z. B. Glühlampenfaden)
-
Zweigängige Schraube und Modell der DNA, Doppelhelix
-
Helix-Struktur in der Fassade des Art Tower Mito
-
Torusförmig gebogene Endlosdoppelhelix – aus zwei diskreten Helices, jede mit 6 Gängen
-
Schraubenfeder – Ganghöhenreduktion an beiden Enden
-
Rechtsgängige Helix der Echten Zaunwinde, Steigung ungefähr 60°
-
Linksgängige Helix eines Windenknöterichs (Fallopia)
-
Rechtsgängige Wendelbohrer; v. l. n. r.: Zweigängige 8-mm-Bohrer für Holz, Metall und Beton sowie ein Zentrierbohrer
-
Wendelförmig gewundener Plasmakern (gelb) eines Stellarators, hier des Experimental-Fusionsreaktor Wendelstein 7-X
-
Schraubenförmige Massenbewegung im äußeren Erdkern als Folge der Corioliskraft
-
Flugbahn eines geladenen Teilchens in einem inhomogenen Magnetfeld
-
Dreiteilung des Winkels mit zwei Helices (hellblau und grün)
-
Tetraeder-Helix, Tetrahelix, Boerdijk-Coxeter Helix
Helix in der Kunst[Bearbeiten | Quelltext bearbeiten]
Von 1970 bis 1973 schuf Louis Constantin die mit 9 Metern Länge und drei Metern Durchmesser größte freitragende Kunststoffskulptur in München, die »Blaue Spirale«.
-
Blaue Spirale
Siehe auch[Bearbeiten | Quelltext bearbeiten]
- Schraublinie (Darstellende Geometrie)
- Schraubfläche
- Helizität
- Chiralität (Chemie)
- Chiralität (Mathematik)
Weblinks[Bearbeiten | Quelltext bearbeiten]
- www.wissenschaft.de: Warum die Natur die Helix so liebt
- Frieda Nugel, Die Schraubenlinie, Dissertation Universität Halle-Wittenberg 1912
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Marc Gingras, Guy Félix, Romain Peresutti: One hundred years of helicene chemistry. Part 2: stereoselective syntheses and chiral separations of carbohelicenes. In: Chemical Society Reviews. Band 42, 2013, S. 1007–1050, doi:10.1039/C2CS35111K.
- ↑ Ars Electronica Festival in alter Post, ORF.at, 13. Mai 2015, zuletzt abgerufen am 10. August 2016. – Bild einer Reihe von Sortierschnecken.
- ↑ Lüftungsrohr auf dem Gehweg r-hol, flickr.com, 5. Dezember 2010, abgerufen am 10. August 2016.
- ↑ https://www.nwpipe.com/about/ Northwest Pipe Company, Vancouver WA, USA – Hersteller von Wendelrohr mit 12–156 Zoll Außendurchmesser.