Grenzzyklus
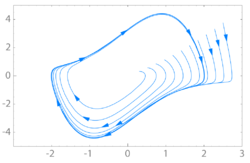
Ein Grenzzyklus oder Limit Cycle ist in der Mathematik und der Theorie dynamischer Systeme eine isolierte periodische Lösung eines autonomen Differentialgleichungssystems.[1]
Betrachtet man die Lösungen des Differentialgleichungssystems als Kurven im Phasenraum, so ist der Grenzzyklus eine geschlossene Kurve (Zyklus), auf die benachbarte Trajektorien im Grenzwert unendlicher Zeit zulaufen oder von der sie sich entfernen:
- Laufen benachbarte Trajektorien im Grenzwert unendlicher Zeit auf den Grenzzyklus zu, so ist der Grenzzyklus ein eindimensionaler Attraktor und wird stabil genannt.
- Entfernen sich benachbarte Trajektorien dagegen im Grenzwert unendlicher Zeit (bzw. laufen im Grenzwert unendlich negativer Zeit auf den Grenzzyklus zu), so ist der Grenzzyklus ein eindimensionaler Repellor bzw. negativer Attraktor und wird instabil genannt.
Falls benachbarte Lösungen selbst auch periodische Lösungen sind, so handelt es sich nicht um einen Grenzzyklus, da er keine isolierte periodische Lösung darstellt.
In der Ebene macht der Satz von Poincaré-Bendixson Aussagen über die Existenz von Grenzzyklen. Grenzzyklen wurden zuerst von Henri Poincaré studiert.
Bei konservativen dynamischen Systemen und speziell dynamischen Systemen , in denen sich F als Gradient einer Potentialfunktion ausdrücken lässt, gibt es keine Grenzzyklen.[2]
Offenes Problem[Bearbeiten | Quelltext bearbeiten]
Der zweite Teil des 16. Hilbertproblems fragt nach einer oberen Grenze für die Anzahl der Grenzzyklen (und Aussagen über ihre relative Lage) für autonome Differentialgleichungssysteme in der Ebene
wobei P, Q Polynome vom Grad n sind.
Das Problem wurde auch von Stephen Smale in seine Liste offener Probleme aufgenommen, der es neben der Riemann-Vermutung für das am wenigsten greifbare der Hilbertprobleme hält. Smale schränkte das Problem weiter ein: P und Q seien Polynome vom maximalen Grad d; gibt es eine obere Schranke für die Anzahl der Grenzzyklen mit einer universellen Konstante ? Bekannt ist, dass die Anzahl endlich ist (Juli Iljaschenko, Jean Écalle, nach Vorarbeiten von Henri Dulac).
Einführung anhand zweier Beispiele[Bearbeiten | Quelltext bearbeiten]

Dynamische Systeme sind Systeme autonomer Differentialgleichungen der Form:
Die Lösung dieser Differentialgleichungen werden Trajektorien genannt und beschreiben das Verhalten/die Entwicklung des Systems in der Zeit t. In der Theorie dynamischer Systeme ist die asymptotische Stabilität solcher Lösungen von Interesse, also ihr Verhalten im zeitlichen Grenzwert . Ergeben sich im genannten Grenzwert oszillierende Lösungen des Systems, so spiegeln sie sich als zyklische, geschlossene Kurve in diesem Phasenraum wider; sie wird Grenzzyklus genannt.
Wenn sich andere Trajektorien (mit unterschiedlichen Startbedingungen) dieser geschlossenen Kurve für große Zeiten t immer weiter annähern („hineinspiralen“), so handelt es sich um einen Attraktor („Anzieher“) bzw. stabilen Grenzzyklus. Ein klassisches Beispiel hierfür ist der Van-der-Pol-Oszillator, dessen Phasenraumportrait in obiger Abbildung gezeigt ist.
Entfernen sich alle Trajektorien für vom Grenzzyklus, so wird er instabil oder auch Repeller genannt.
Ein einfaches mathematisches Pendel hingegen hat zwar periodische Trajektorien, aber keinen Grenzzyklus. Das sieht man in nebenstehender Abbildung daran, dass sich keine Trajektorien an die Zyklen annähern bzw. von ihnen entfernen, d. h. die Zyklen nicht isoliert auftreten. Nicht isoliert bedeutet hier, dass in jeder Umgebung eines Zyklus wieder andere Zyklen liegen.
Stabilität[Bearbeiten | Quelltext bearbeiten]

Die Stabilität eines Grenzzyklus der Periode T wird durch seine Floquet-Multiplikatoren bestimmt.
Der Grenzzyklus entspricht einem Fixpunkt in der Poincaré-Abbildung. Die Poincaré-Abbildung gewinnt man durch einen Schnitt (Poincaré-Schnitt) im Phasenraum, so dass der Grenzzyklus die Schnittebene senkrecht mit seiner Periode durchstößt (siehe blaue Schnittebene in nebenstehender Abbildung).
Die Stabilität des Grenzzyklus entspricht nun der Stabilität des Fixpunktes seiner Poincaré-Abbildung P.[3]
Sei x* der Fixpunkt von P, so gilt .
Für einen Punkt x, der nahe am Fixpunkt liegt, also , gilt nun die Abbildung
mit k dem k-ten Durchstoßen des Poincaré-Schnittes.
Unter der Annahme, dass klein ist, kann P in der Nähe von x* als linear angenommen werden (DP(x*) ist die Jacobimatrix von P an x*), und es folgt
- .
Die Eigenwerte von DP(x*) bestimmen nun die Stabilität von x* und werden Floquet-Multiplikatoren des Grenzzyklus genannt. Einer der Floquet-Multiplikatoren ist immer 1 und entspricht der Richtung der Bewegung auf dem Grenzzyklus; dieser Multiplikator wird Goldstone Mode genannt.[4]
- falls alle anderen Multiplikatoren vom Betrag her kleiner 1 sind (d. h. für alle i außer dem Goldstone Mode), so ist der Grenzzyklus asymptotisch stabil;
- falls ist für alle i außer dem Goldstone Mode, so ist der Grenzzyklus instabil.
Neben stabilen und instabilen Grenzzyklen gibt es auch semistabile Grenzzyklen, d. h. außen liegende Trajektorien spiralen auf den Grenzzyklus zu und innen liegende spiralen von ihm weg (oder umgekehrt).[5]
Hopf-Bifurkation[Bearbeiten | Quelltext bearbeiten]

Grenzzyklen entstehen generisch aus Hopf-Bifurkationen. Betrachtet man eine Lösung eines Systems von Differentialgleichungen mit einem freien Parameter und verändert diesen stetig, so können Bifurkationspunkte auftreten, d. h. die betrachtete Lösung verändert sich qualitativ. Aus einem Fixpunkt kann so ein Grenzzyklus entstehen und andersherum.
Ein Beispiel ist das Anschalten eines Lasers:
- Solange der Pumpstrom unterhalb des Schwellstroms liegt, leuchtet der Laser nicht, d. h. das ausgestrahlte elektrische Feld ist und ein stabiler Fixpunkt.
- Sobald der Schwellstrom jedoch überschritten wird, fängt der Laser an zu leuchten, es gilt und es handelt sich hier um einen stabilen Grenzzyklus mit der Periode . Die bei auftretende Bifurkation ist daher eine superkritische Hopf-Bifurkation.

Anwendung[Bearbeiten | Quelltext bearbeiten]
Grenzzyklen werden in vielen naturwissenschaftlichen Modellen von Systemen mit selbsterhaltenden Oszillationen verwendet. Einige Beispiele:
- Das Hodgkin–Huxley-Modell für neuronale Aktionspotenziale.
- Das Sel'kov-Modell für Glykolyse.[6]
- Die täglichen Hormon- und Temperaturschwankungen von Tieren.[7][8]
- Die Migration von Krebszellen in begrenzten Mikroumgebungen.[9]
Quellen[Bearbeiten | Quelltext bearbeiten]
- ↑ Definition von Grenzzyklus auf PlanetMath.org (englisch)
- ↑ Zum Beispiel Johnstone, Limit cycles, van der Pol oscillator and Poincaré-Bendixson theorem, pdf
- ↑ K. T. Chau, Zheng Wang: Chaos in Electric Drive Systems: Analysis, Control and Application. John Wiley & Sons, 2011, ISBN 978-0-470-82836-6 (google.de [abgerufen am 7. August 2012]).
- ↑ Valentin Flunkert: Delay-Coupled Complex Systems: and Applications to Lasers. Springer, 2011, ISBN 978-3-642-20249-0, S. 159– (google.de [abgerufen am 7. August 2012])., man beachte die Beziehung zwischen Floquet-Exponent und Floquet-Multiplikator mit der Periode T des Grenzzyklus.
- ↑ Richard H. Enns, George McGuire: Nonlinear Physics With Maple for Scientists and Engineers. Springer, 2000, ISBN 978-0-8176-4119-1, S. 260– (google.de [abgerufen am 7. August 2012]).
- ↑ E. E. Sel'kov: Self-Oscillations in Glycolysis 1. A Simple Kinetic Model. In: European Journal of Biochemistry. 4. Jahrgang, Nr. 1, 1968, S. 79–86, doi:10.1111/j.1432-1033.1968.tb00175.x (englisch).
- ↑ Jean-Christophe Leloup, Didier Gonze, Albert Goldbeter: Limit Cycle Models for Circadian Rhythms Based on Transcriptional Regulation in Drosophila and Neurospora. In: Journal of Biological Rhythms. 14. Jahrgang, Nr. 6, 1. Dezember 1999, S. 433–448, doi:10.1177/074873099129000948 (englisch).
- ↑ Till Roenneberg, Elaine Jane Chua, Ric Bernardo, Eduardo Mendoza: Modelling Biological Rhythms. In: Current Biology. 18. Jahrgang, Nr. 17, 9. September 2008, S. R826–R835, doi:10.1016/j.cub.2008.07.017 (sciencedirect.com).
- ↑ David B. Brückner, Alexandra Fink, Christoph Schreiber, Peter J. F. Röttgermann, Joachim Rädler, Chase P. Broedersz: Stochastic nonlinear dynamics of confined cell migration in two-state systems. In: Nature Physics. 15. Jahrgang, Nr. 6, 2019, S. 595–601, doi:10.1038/s41567-019-0445-4 (englisch).
Literatur[Bearbeiten | Quelltext bearbeiten]
- Cristoforo Sergio Bertuglia; Franco Vaio: Nonlinearity, chaos, and complexity: the dynamics of natural and social systems Oxford; New York: Oxford University Press, 2005, ISBN 978-0-19-856790-5





















